4.1 对数及其运算(一)课件18张PPT
文档属性
| 名称 | 4.1 对数及其运算(一)课件18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览






文档简介
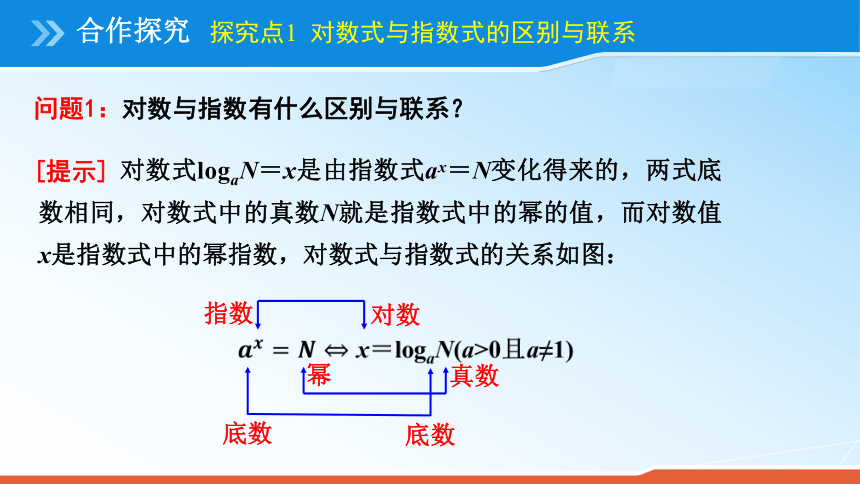
课件18张PPT。对数与对数运算第一课时 对数学习目标1.了解对数、常用对数、自然对数的概念.3.理解和掌握对数的性质,会求简单的对数值.2.会用对数的定义进行对数式与指数式的互化.预习清单知识点一 对数的概念1.对数的概念
一般地,若ax=N(a>0,且a≠1),那么数x叫做 ,记作 ,其中a叫做对数的 ,N叫做 .以a为底N的对数x=logaN底数真数预习清单知识点二 常用对数和自然对数的定义2.常用对数、自然对数的定义常用对数:通常我们将以 为底数的对数叫做常用对数.为了简便,N的常用对数log10N简记作 .自然对数:在科学技术中常使用以无理数e=2.718 28…为底数的对数,以 为底的对数称为 ,并且把logeN记作 .10lg Neln N自然对数(1)1的对数为????????,即loga1=0;(2)底的对数为??????,即logaa=1;(3)零和负数???????????????????.预习清单知识点三 对数的性质3.对数的性质:零 1 没有对数 对数式logaN=x是由指数式ax=N变化得来的,两式底数相同,对数式中的真数N就是指数式中的幂的值,而对数值x是指数式中的幂指数,对数式与指数式的关系如图:合作探究探究点1 对数式与指数式的区别与联系问题1:对数与指数有什么区别与联系?[提示]?底数底数真数幂指数对数合作探究探究点2 对数式中底数和真数的要求问题2:对数logaN中,a与N有什么要求,为什么?[提示] 要求:a>0,a≠1,且N >0.这是由于对数式中的底数a就是指数式中的底数a,所以a的取值范围为a>0,且a≠1;由于在指数式中ax=N,而ax>0,所以N>0,即负数和零没有对数.典例精讲:题型一:对数式和指数式相互转化【例1】将下列指数式化为对数式,对数式化为指数式:?[解析]??(3) lg0.1=-1; ??题后反思(2)注意字母位置的对应关系,对数式中的真数N就是指数式中的幂的值,而对数值x是指数式中的幂指数.(1)底数相同;方法总结:指数式和对数式互化的要点:典例精讲:题型二:对数式求值?[解析](1)设log464=x,则4x=64,(2)设log31=x,则3x=1,[分析] 求对数式的值,可以设其为x,将之转化为指数式求解. ∴log464=3.∵64=43,∴x=3,∴log31=0.∵1=30,∴x=0,典例精讲:题型二:对数式求值??(4)设log927=x,则9x=27,??即32x=33,∴2x=3,??典例精讲:题型三:解对数方程??(2)x6=8,x>0,?????典例精讲:题型三:解对数方程?(3)由题10x=100,∵102=100,∴x=2.(4)由题e-x=e2,∴x=-2.题后反思方法总结:?课堂练习1.如果a3=N(a>1且a≠1),则有( )
A.log3N=a B.log3a=N
C.logNa=3 D.logaN=3答案: D课堂练习2.在M=log(5-a)(a-2)中,求实收a的取值范围.?解析:要使log(5-a)(a-2)有意义,只须使:归纳小结1.对数的定义:若ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,
记作x=logaN,其中a叫做对数的底数,N叫做真数.2.对数符号logaN只有在a>0,a≠1且N>0时才有意义.3.抓住指数式与对数式的关系,指数运算和对数运算互为逆运算.
一般地,若ax=N(a>0,且a≠1),那么数x叫做 ,记作 ,其中a叫做对数的 ,N叫做 .以a为底N的对数x=logaN底数真数预习清单知识点二 常用对数和自然对数的定义2.常用对数、自然对数的定义常用对数:通常我们将以 为底数的对数叫做常用对数.为了简便,N的常用对数log10N简记作 .自然对数:在科学技术中常使用以无理数e=2.718 28…为底数的对数,以 为底的对数称为 ,并且把logeN记作 .10lg Neln N自然对数(1)1的对数为????????,即loga1=0;(2)底的对数为??????,即logaa=1;(3)零和负数???????????????????.预习清单知识点三 对数的性质3.对数的性质:零 1 没有对数 对数式logaN=x是由指数式ax=N变化得来的,两式底数相同,对数式中的真数N就是指数式中的幂的值,而对数值x是指数式中的幂指数,对数式与指数式的关系如图:合作探究探究点1 对数式与指数式的区别与联系问题1:对数与指数有什么区别与联系?[提示]?底数底数真数幂指数对数合作探究探究点2 对数式中底数和真数的要求问题2:对数logaN中,a与N有什么要求,为什么?[提示] 要求:a>0,a≠1,且N >0.这是由于对数式中的底数a就是指数式中的底数a,所以a的取值范围为a>0,且a≠1;由于在指数式中ax=N,而ax>0,所以N>0,即负数和零没有对数.典例精讲:题型一:对数式和指数式相互转化【例1】将下列指数式化为对数式,对数式化为指数式:?[解析]??(3) lg0.1=-1; ??题后反思(2)注意字母位置的对应关系,对数式中的真数N就是指数式中的幂的值,而对数值x是指数式中的幂指数.(1)底数相同;方法总结:指数式和对数式互化的要点:典例精讲:题型二:对数式求值?[解析](1)设log464=x,则4x=64,(2)设log31=x,则3x=1,[分析] 求对数式的值,可以设其为x,将之转化为指数式求解. ∴log464=3.∵64=43,∴x=3,∴log31=0.∵1=30,∴x=0,典例精讲:题型二:对数式求值??(4)设log927=x,则9x=27,??即32x=33,∴2x=3,??典例精讲:题型三:解对数方程??(2)x6=8,x>0,?????典例精讲:题型三:解对数方程?(3)由题10x=100,∵102=100,∴x=2.(4)由题e-x=e2,∴x=-2.题后反思方法总结:?课堂练习1.如果a3=N(a>1且a≠1),则有( )
A.log3N=a B.log3a=N
C.logNa=3 D.logaN=3答案: D课堂练习2.在M=log(5-a)(a-2)中,求实收a的取值范围.?解析:要使log(5-a)(a-2)有意义,只须使:归纳小结1.对数的定义:若ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,
记作x=logaN,其中a叫做对数的底数,N叫做真数.2.对数符号logaN只有在a>0,a≠1且N>0时才有意义.3.抓住指数式与对数式的关系,指数运算和对数运算互为逆运算.
