5.1 对数函数的概念课件17张PPT
文档属性
| 名称 | 5.1 对数函数的概念课件17张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 584.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 21:37:02 | ||
图片预览






文档简介
课件17张PPT。 问题提出:
由前面的学习我们知道:有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,··· 1个这样的细胞分裂x次会得到多少个细胞?如果知道了细胞的个数y如何确定分裂的次数x呢?由对数式与指数式的互化可知:上式可以看作以y自变量的函数表达式吗??预备知识2、对数的概念
一般地,如果a b=N,那么数 b叫做以a为底 N的对数,记作 b=㏒a N,a叫做对数的底数,N叫做真数.3、指数函数的定义: 形如y = ax (a?0,且a ?1)的函数叫做指数函数,
其中x是自变量 .定义域是R .1、函数的概念 对于每一个给定的y值都有惟一的x的值与之对应,把y看作自变量,x就是y的函数,但习惯上仍用x表示自变量,y表示它的函数:即这就是本节课要学习的:对数函数及其性质本节课的学习预告:1.对数函数的定义
2.画出对数函数的图象
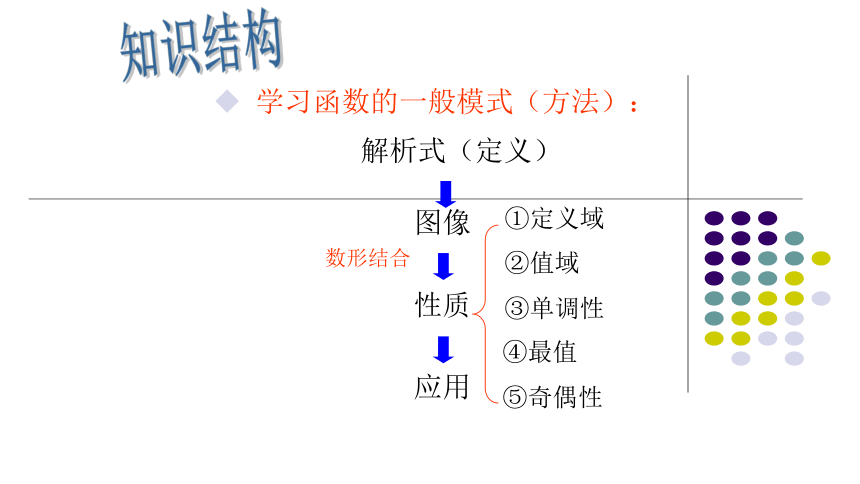
3.对数函数性质的探究 一般地,函数y = loga x (a>0,且a≠ 1)叫做对数函数.其中 x是自变量, 函数的定义域是( 0 , +∞)值域R(1){x|x≠0}(2){x|x<4} (3){x|x>1} (4){x|x>0且x≠1}一、对数函数的概念 学习函数的一般模式(方法):解析式(定义)图像性质应用数形结合①定义域②值域③单调性⑤奇偶性④最值知识结构用描点法画出对数函数
的图象。作图步骤: ①列表,
②描点,
③连线。二、对数函数的图像图 象 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点在(0,+∞)上是在(0,+∞)上是( 0,+∞)R
(1 ,0), 即当x =1时,y=0增函数减函数y>0y=0y<0 y<0y=0y>0 补充性质二底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形101时, 底数越大,其图象越接近x轴。 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7 log23.4log28.5∴ log23.4< log28.5解法1:画图找点比高低解法2:利用对数函数的单调性考察函数y=log 2 x ,∵a=2 > 1,∴函数在区间(0,+∞)
上是增函数;∵3.4<8.5∴ log23.4< log28.5我练练我掌握 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7解法2:考察函数y=log 0.3 x ,
∵a=0.3< 1,
∴函数在区间(0,+∞)上是减函数;
∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7 (2)解法1:画图找点比高低我练练我掌握 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7小
结比较两个同底对数值的大小时:1.观察底数是大于1还是小于1( a>1时为增函数
0即0 1 比较下列各组中,两个值的大小:
(3) loga5.1与 loga5.9解: ①若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
②若0 ∴ loga5.1 > loga5.9我练练我掌握 比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 . 解: ⑴∵log67>log66=1
log76<log77=1
∴ log67>log76 ⑵ ∵log3π>log31=0
log20.8<log21=0
∴ log3π>log20.8 注意:利用对数函数的增减性比较两个对数的大小.当不能直接进行比较时,可在两个对数中间插入一个已知数(如1或0等),间接比较上述两个对数的大小提示 : log aa=1提示: log a1=0我分析我发展课堂小结
1、对数函数的概念;
2、反函数的概念.对数函数课堂作业: 习题3-5 A组1、3课堂练习:P91 1,2,3,4。
由前面的学习我们知道:有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,··· 1个这样的细胞分裂x次会得到多少个细胞?如果知道了细胞的个数y如何确定分裂的次数x呢?由对数式与指数式的互化可知:上式可以看作以y自变量的函数表达式吗??预备知识2、对数的概念
一般地,如果a b=N,那么数 b叫做以a为底 N的对数,记作 b=㏒a N,a叫做对数的底数,N叫做真数.3、指数函数的定义: 形如y = ax (a?0,且a ?1)的函数叫做指数函数,
其中x是自变量 .定义域是R .1、函数的概念 对于每一个给定的y值都有惟一的x的值与之对应,把y看作自变量,x就是y的函数,但习惯上仍用x表示自变量,y表示它的函数:即这就是本节课要学习的:对数函数及其性质本节课的学习预告:1.对数函数的定义
2.画出对数函数的图象
3.对数函数性质的探究 一般地,函数y = loga x (a>0,且a≠ 1)叫做对数函数.其中 x是自变量, 函数的定义域是( 0 , +∞)值域R(1){x|x≠0}(2){x|x<4} (3){x|x>1} (4){x|x>0且x≠1}一、对数函数的概念 学习函数的一般模式(方法):解析式(定义)图像性质应用数形结合①定义域②值域③单调性⑤奇偶性④最值知识结构用描点法画出对数函数
的图象。作图步骤: ①列表,
②描点,
③连线。二、对数函数的图像图 象 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点在(0,+∞)上是在(0,+∞)上是( 0,+∞)R
(1 ,0), 即当x =1时,y=0增函数减函数y>0y=0y<0 y<0y=0y>0 补充性质二底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形10
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7 log23.4log28.5∴ log23.4< log28.5解法1:画图找点比高低解法2:利用对数函数的单调性考察函数y=log 2 x ,∵a=2 > 1,∴函数在区间(0,+∞)
上是增函数;∵3.4<8.5∴ log23.4< log28.5我练练我掌握 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7解法2:考察函数y=log 0.3 x ,
∵a=0.3< 1,
∴函数在区间(0,+∞)上是减函数;
∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7 (2)解法1:画图找点比高低我练练我掌握 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7小
结比较两个同底对数值的大小时:1.观察底数是大于1还是小于1( a>1时为增函数
0
(3) loga5.1与 loga5.9解: ①若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
②若0
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 . 解: ⑴∵log67>log66=1
log76<log77=1
∴ log67>log76 ⑵ ∵log3π>log31=0
log20.8<log21=0
∴ log3π>log20.8 注意:利用对数函数的增减性比较两个对数的大小.当不能直接进行比较时,可在两个对数中间插入一个已知数(如1或0等),间接比较上述两个对数的大小提示 : log aa=1提示: log a1=0我分析我发展课堂小结
1、对数函数的概念;
2、反函数的概念.对数函数课堂作业: 习题3-5 A组1、3课堂练习:P91 1,2,3,4。
