5.3 对数函数的图像和性质课件17张PPT
文档属性
| 名称 | 5.3 对数函数的图像和性质课件17张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 611.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 21:38:42 | ||
图片预览



文档简介
课件17张PPT。高一数学北师大版必修一
第三章第五节对数函数和性质1.对数函数的概念: 我们把 叫作对数函数, 其中定义域是 ,值域是 , 叫作对数函数 的底数.2.指数函数 和对数函数
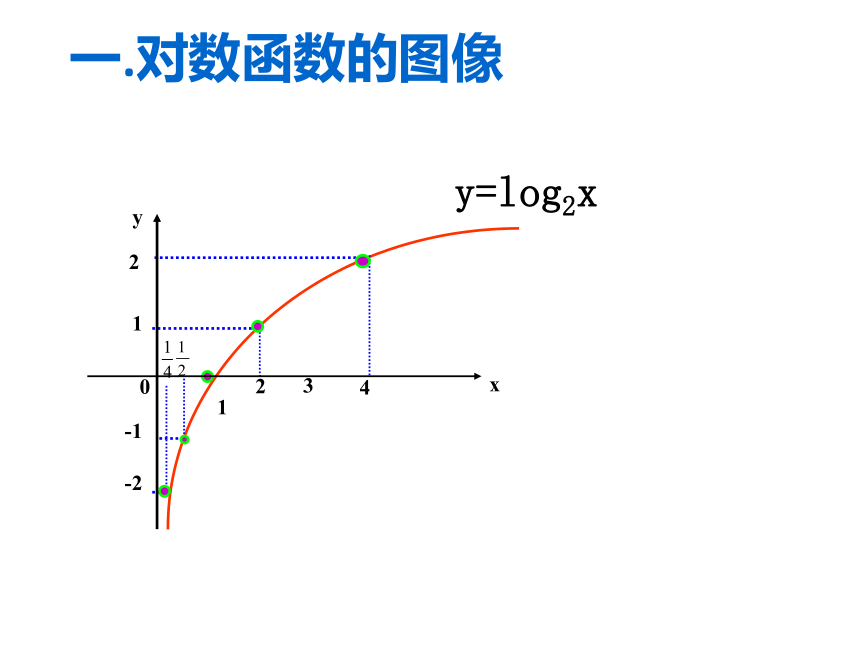
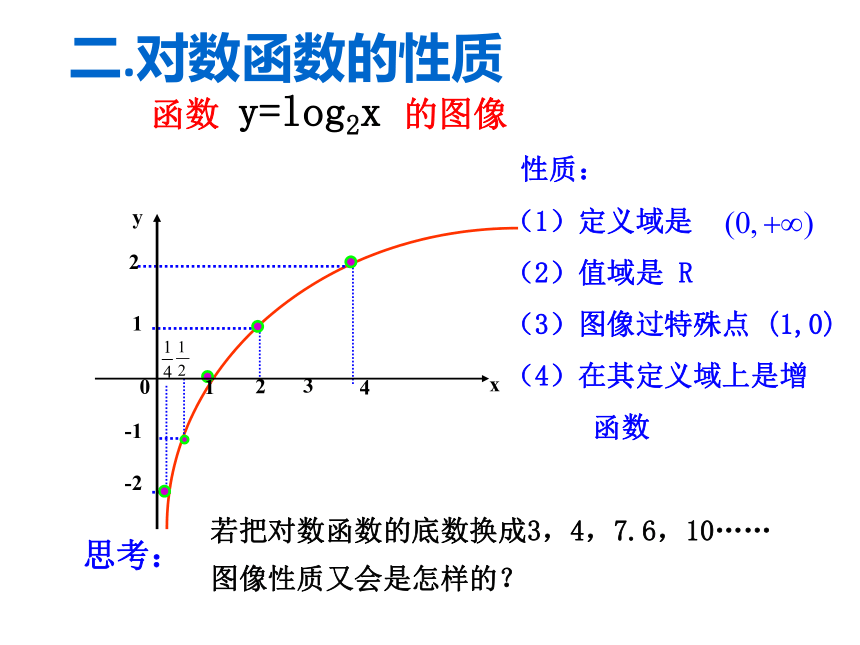
互为反函数。y=logax (a>0,且a≠1) R一.对数函数的图像合作探究 y=log2x一.对数函数的图像一.对数函数的图像函数 y=log2x 的图像思考: 性质:
(1)定义域是
(2)值域是 R
(3)图像过特殊点 (1,0)
(4)在其定义域上是增
函数若把对数函数的底数换成3,4,7.6,10……图像性质又会是怎样的?
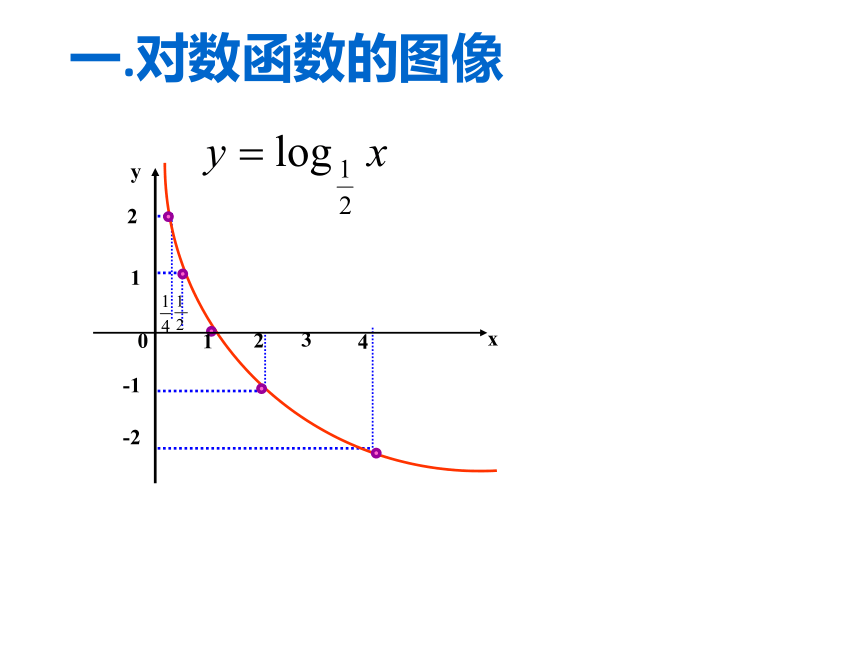
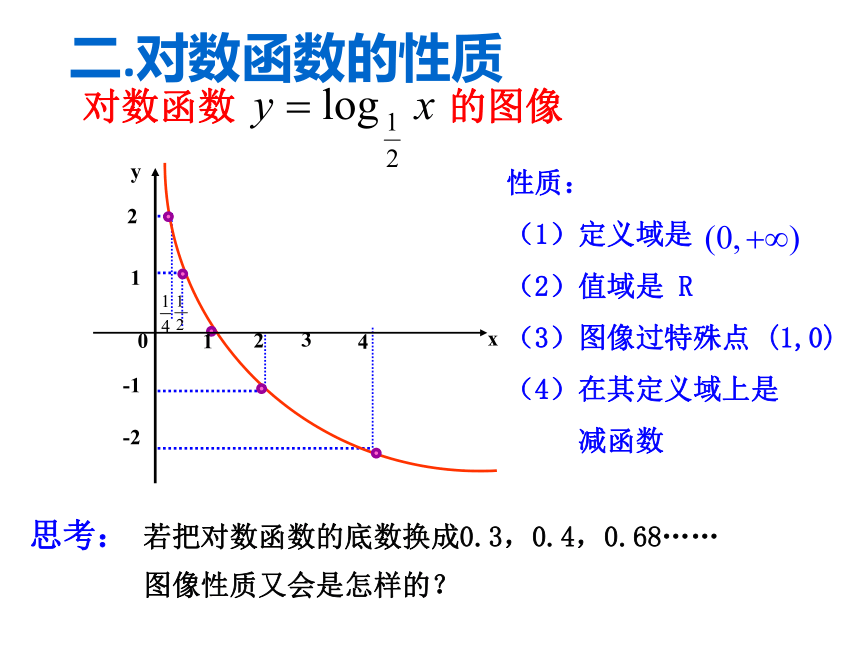
二.对数函数的性质对数函数 的图像若把对数函数的底数换成0.3,0.4,0.68……图像性质又会是怎样的?思考:性质:
(1)定义域是
(2)值域是 R
(3)图像过特殊点 (1,0)
(4)在其定义域上是
减函数二.对数函数的性质图 像 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点在(0,+∞)上是在(0,+∞)上是对数函数y=logax (a>0,且a≠1) 的图像与性质( 0,+∞)R(1 ,0), 即当x =1时,y=0增函数减函数y>0y=0y<0 y<0y=0y>0 1例1. 求下列函数定义域:
(1)y=㏒a x2 ; (2) y=㏒a (4-x)解 (1)因为 x2 >0, 即x≠0,所以函数的定义域为{x| x≠0 };
(2)因为4-x>0即x<4,所以函数的定义域为{x| x<4}.三.例题练一练:求函数的定义域
{x| 0(1)㏒25.3, ㏒24.7 (2) ㏒ 0.27,㏒0.29
(3) ㏒a 3.1,㏒a5.2 (a>0,a≠1) 解(1)因为2>1,函数y=㏒2 x是增函数,
5.3>4.7, 所以 ㏒25.3>㏒24.7;
(2)因为0<0.2<1,函数y=㏒0.2x是减函数,
7<9, 所以㏒ 0.27>㏒0.29;
(3)当a>1时,函数y=㏒ax在(0, +∞)上为增函数,
此时 , ㏒a 3.1<㏒a5.2
当0 此时, ㏒a 3.1>㏒a5.2 1例3 . 比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 .
解: ⑴ ∵ log67>log66=1
log20.8<log21=0
思考:如何比较两个对数的大小?
同底时利用对数函数的增减性比较两个对数的大小。
2. 不同底时可在两个对数中间插入一 个已知数(如1或0等),间接比较上述两个对数的大小。提示 : log aa=1提示: log a1=0 log76<log77=1
∴ log67>log76⑵ ∵ log3π>log31=0 ∴ log3π>log20.8变式训练:
1.下列不等式,比较正数m,n的大小已知
⑴ log2m < log2n
⑵ log0.5m < log0.5n
⑶ logam > logan (a>0,且a≠1)
2.解关于x的不等式
在同一坐标系中用描点法画出对数函数
的图像。
说说图像间有什么关系?你能得出什么结论?a=2一般的,函数y=f(x)与它的
反函数图像关于直线y=x对称P(m,n)Q(n,m)-2 -1 0 1 2 0.25 0.5 1 2 4 这两个函数互为反函数,则对于函数
图像上任意一点P(m,n), 它关于直线 的对称点Q(n,m)总在函数
的图像上,所以这两个函数的图像关于直线 对称。1.函数 的定义域为______________。2.函数 的定义域为_____________。3.比较下列各题中两个数的大小课堂练习{x|x>2}
{x|x≥2}
4. 解不等式:课堂小结:1.对数函数的图象和性质(表格)
2.性质的初步应用一. 知识点二. 思想方法1. 数形结合思想3. 分类讨论思想2. 从特殊到一般的化归思想作业:P97 习题3-5集 A组
第3、4、5题
第三章第五节对数函数和性质1.对数函数的概念: 我们把 叫作对数函数, 其中定义域是 ,值域是 , 叫作对数函数 的底数.2.指数函数 和对数函数
互为反函数。y=logax (a>0,且a≠1) R一.对数函数的图像合作探究 y=log2x一.对数函数的图像一.对数函数的图像函数 y=log2x 的图像思考: 性质:
(1)定义域是
(2)值域是 R
(3)图像过特殊点 (1,0)
(4)在其定义域上是增
函数若把对数函数的底数换成3,4,7.6,10……图像性质又会是怎样的?
二.对数函数的性质对数函数 的图像若把对数函数的底数换成0.3,0.4,0.68……图像性质又会是怎样的?思考:性质:
(1)定义域是
(2)值域是 R
(3)图像过特殊点 (1,0)
(4)在其定义域上是
减函数二.对数函数的性质图 像 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点在(0,+∞)上是在(0,+∞)上是对数函数y=logax (a>0,且a≠1) 的图像与性质( 0,+∞)R(1 ,0), 即当x =1时,y=0增函数减函数y>0y=0y<0 y<0y=0y>0 1例1. 求下列函数定义域:
(1)y=㏒a x2 ; (2) y=㏒a (4-x)解 (1)因为 x2 >0, 即x≠0,所以函数的定义域为{x| x≠0 };
(2)因为4-x>0即x<4,所以函数的定义域为{x| x<4}.三.例题练一练:求函数的定义域
{x| 0
(3) ㏒a 3.1,㏒a5.2 (a>0,a≠1) 解(1)因为2>1,函数y=㏒2 x是增函数,
5.3>4.7, 所以 ㏒25.3>㏒24.7;
(2)因为0<0.2<1,函数y=㏒0.2x是减函数,
7<9, 所以㏒ 0.27>㏒0.29;
(3)当a>1时,函数y=㏒ax在(0, +∞)上为增函数,
此时 , ㏒a 3.1<㏒a5.2
当0
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 .
解: ⑴ ∵ log67>log66=1
log20.8<log21=0
思考:如何比较两个对数的大小?
同底时利用对数函数的增减性比较两个对数的大小。
2. 不同底时可在两个对数中间插入一 个已知数(如1或0等),间接比较上述两个对数的大小。提示 : log aa=1提示: log a1=0 log76<log77=1
∴ log67>log76⑵ ∵ log3π>log31=0 ∴ log3π>log20.8变式训练:
1.下列不等式,比较正数m,n的大小已知
⑴ log2m < log2n
⑵ log0.5m < log0.5n
⑶ logam > logan (a>0,且a≠1)
2.解关于x的不等式
在同一坐标系中用描点法画出对数函数
的图像。
说说图像间有什么关系?你能得出什么结论?a=2一般的,函数y=f(x)与它的
反函数图像关于直线y=x对称P(m,n)Q(n,m)-2 -1 0 1 2 0.25 0.5 1 2 4 这两个函数互为反函数,则对于函数
图像上任意一点P(m,n), 它关于直线 的对称点Q(n,m)总在函数
的图像上,所以这两个函数的图像关于直线 对称。1.函数 的定义域为______________。2.函数 的定义域为_____________。3.比较下列各题中两个数的大小课堂练习{x|x>2}
{x|x≥2}
4. 解不等式:课堂小结:1.对数函数的图象和性质(表格)
2.性质的初步应用一. 知识点二. 思想方法1. 数形结合思想3. 分类讨论思想2. 从特殊到一般的化归思想作业:P97 习题3-5集 A组
第3、4、5题
