5.3 对数函数的图像和性质课件31张PPT
文档属性
| 名称 | 5.3 对数函数的图像和性质课件31张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 963.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 21:40:09 | ||
图片预览







文档简介
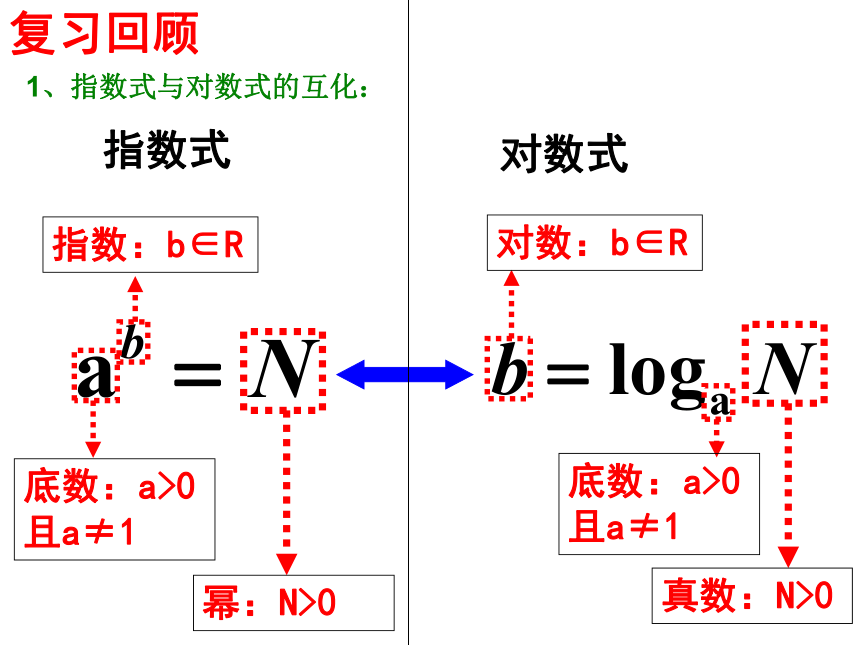
课件31张PPT。对 数 函 数 及 其 性 质复习回顾底数:a>0且a≠1幂:N>0真数:N>0底数:a>0且a≠1指数:b∈R对数:b∈R 指数式对数式1、指数式与对数式的互化:2、函数的研究过程定义(解析式)
图像
性质
应用
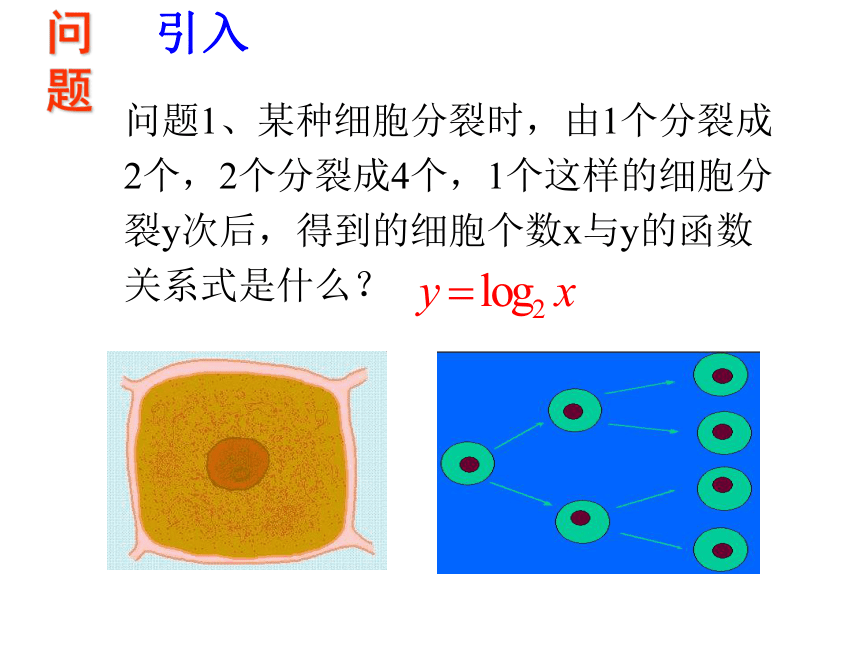
复习回顾引入问题1、某种细胞分裂时,由1个分裂成
2个,2个分裂成4个,1个这样的细胞分
裂y次后,得到的细胞个数x与y的函数
关系式是什么?问题问题2、《庄子·天下篇》中写道:“一尺
之棰,日取其半,万世不竭。”请你写出
截取y次后,木棰剩余量x关于y的函数关
系式? 一般地,形如函数 y = loga x (a>0,且a≠ 1 )叫做对数函数.其中 x是自变量,函数的定义域是( 0 , +∞).对数函数的定义:对数函数对底数的限制条件:
注意: 对数函数y = loga x 解析式特征:
(1)底数:为大于0且不等于1的常数;(2)真数:仅有自变量x;(3)系数: 为+1.三个条件缺一不可
例1.判断下列函数中,是对数函数的是: ( )
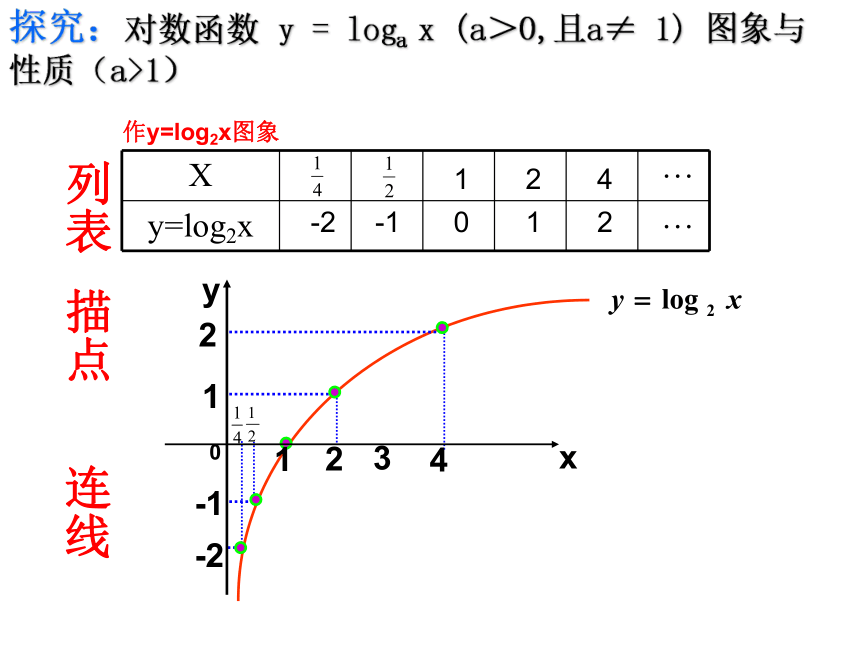
(2) (3)(4)(5)4 (1)列表描点作y=log2x图象连线探究:对数函数 y = loga x (a>0,且a≠ 1) 图象与性质(a>1) 0 1 2 1 4 2 -2 -1 …
…
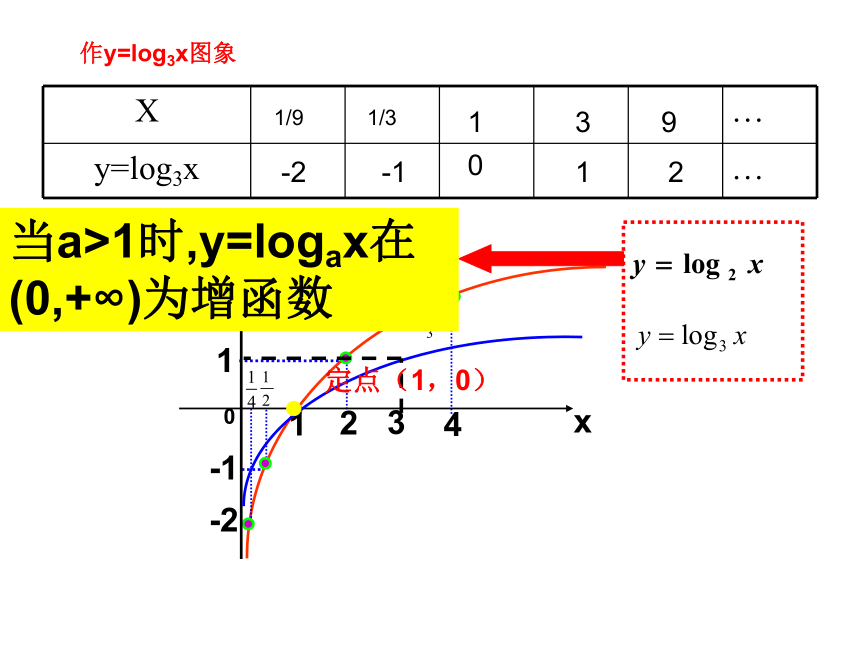
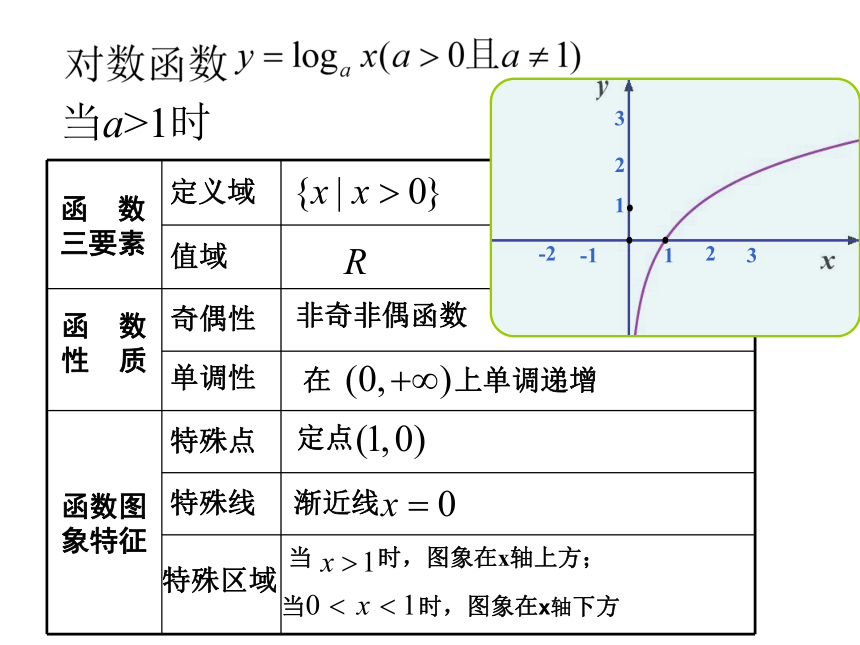
作y=log3x图象910312-1-21/31/9当a>1时,y=logax在(0,+∞)为增函数定点(1,0)函 数三要素函 数性 质函数图象特征定义域值域奇偶性单调性特殊点特殊线特殊区域非奇非偶函数当 时,图象在x轴上方;当 时,图象在x轴下方当a>1时利用换底公式,可以得到:又点(x,y)和点(x,-y)关于___对称
所以,y=log 2 x 与 y= -log 2 x 关于 ____对称X轴 X轴探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质函数 的图象利用对称性作出: 定点(1,0)当00当x=1时,总有loga1=0如:log1.059.8
>0比如:log30.9<0即不论底数在a>1或0当x=1时,总有loga1=0比如:log0.39 <0比如:log0.50.8
>0底数和真数的范围相同,则对数大于0;底数和真数的范围不同,则对数小于0;
同正异负思考:已知下列图像,比较a1,a2, a3, a4的大小y=1x=1yxa4a3a1a2a
由
小
变
大a
由
小
变
大 01a>1时,底越大,图像离坐标轴越近
0构造函数应用举例(5) log56 log65(4) log57 log47(6) log0.67 log0.90.2<><练习:比较下列各组数中两个数的大小:<<>(4)>例3求下列函数的定义域:(1) (2) 解 :由 得 ∴函数 的定义域是课堂小结1、本节课我们学习的新知识:
①、引入新知一定义:底数真数有范围;
②、探究性质两图象:共性异性源于a;
③、比较大小三类型:分型别类原理一
(同底不同真、同真不同底、底真都不同);2、本节课我们用到的数学思想方法:
数形结合、类比、分类讨论、构造函数法作业:
必做作业:《名师伴你行》P48页典例1,3,练习1,3;P50页典例1,练习1,
选做作业:(课后探究)指数函数和对数函数之间有怎样的关系呢?谢谢各位的光临和指导图 象 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点:在(0,+∞)上是:在(0,+∞)上是对数函数y=logax (a>0,且a≠1) 的图象与性质( 0,+∞)R
(1 ,0), 即当x =1时,y=0增函数减函数返回
图像
性质
应用
复习回顾引入问题1、某种细胞分裂时,由1个分裂成
2个,2个分裂成4个,1个这样的细胞分
裂y次后,得到的细胞个数x与y的函数
关系式是什么?问题问题2、《庄子·天下篇》中写道:“一尺
之棰,日取其半,万世不竭。”请你写出
截取y次后,木棰剩余量x关于y的函数关
系式? 一般地,形如函数 y = loga x (a>0,且a≠ 1 )叫做对数函数.其中 x是自变量,函数的定义域是( 0 , +∞).对数函数的定义:对数函数对底数的限制条件:
注意: 对数函数y = loga x 解析式特征:
(1)底数:为大于0且不等于1的常数;(2)真数:仅有自变量x;(3)系数: 为+1.三个条件缺一不可
例1.判断下列函数中,是对数函数的是: ( )
(2) (3)(4)(5)4 (1)列表描点作y=log2x图象连线探究:对数函数 y = loga x (a>0,且a≠ 1) 图象与性质(a>1) 0 1 2 1 4 2 -2 -1 …
…
作y=log3x图象910312-1-21/31/9当a>1时,y=logax在(0,+∞)为增函数定点(1,0)函 数三要素函 数性 质函数图象特征定义域值域奇偶性单调性特殊点特殊线特殊区域非奇非偶函数当 时,图象在x轴上方;当 时,图象在x轴下方当a>1时利用换底公式,可以得到:又点(x,y)和点(x,-y)关于___对称
所以,y=log 2 x 与 y= -log 2 x 关于 ____对称X轴 X轴探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质函数 的图象利用对称性作出: 定点(1,0)当0
>0比如:log30.9<0即不论底数在a>1或0
>0底数和真数的范围相同,则对数大于0;底数和真数的范围不同,则对数小于0;
同正异负思考:已知下列图像,比较a1,a2, a3, a4的大小y=1x=1yxa4a3a1a2a
由
小
变
大a
由
小
变
大 0
①、引入新知一定义:底数真数有范围;
②、探究性质两图象:共性异性源于a;
③、比较大小三类型:分型别类原理一
(同底不同真、同真不同底、底真都不同);2、本节课我们用到的数学思想方法:
数形结合、类比、分类讨论、构造函数法作业:
必做作业:《名师伴你行》P48页典例1,3,练习1,3;P50页典例1,练习1,
选做作业:(课后探究)指数函数和对数函数之间有怎样的关系呢?谢谢各位的光临和指导图 象 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点:在(0,+∞)上是:在(0,+∞)上是对数函数y=logax (a>0,且a≠1) 的图象与性质( 0,+∞)R
(1 ,0), 即当x =1时,y=0增函数减函数返回
