5.1平行关系的判定 课件(18张PPT)
文档属性
| 名称 | 5.1平行关系的判定 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 242.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 21:44:08 | ||
图片预览





文档简介
课件18张PPT。平行关系(1)
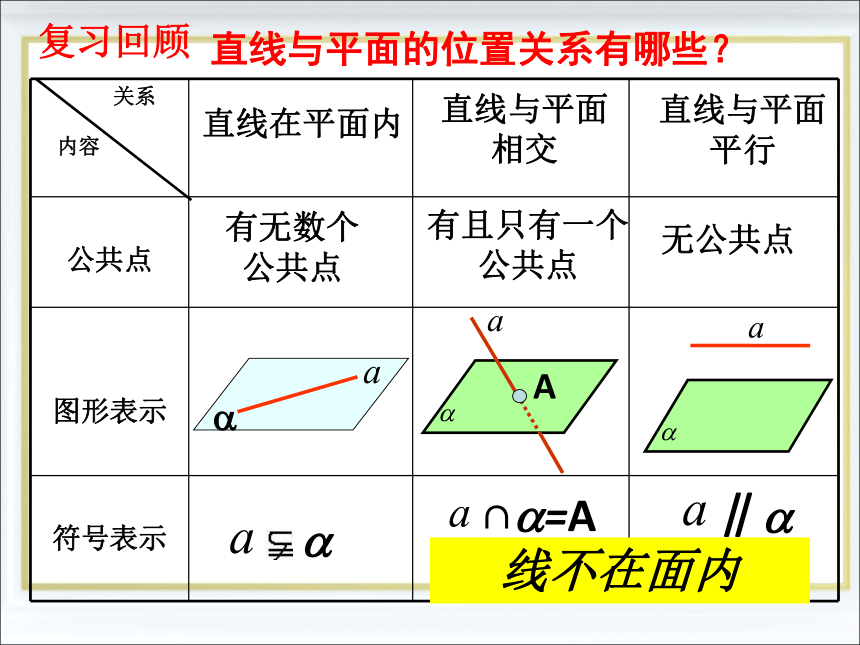
———直线与平面平行的判定内容关系直线在平面内直线与平面
相交直线与平面
平行有无数个
公共点有且只有一个
公共点无公共点 直线与平面的位置关系有哪些?线不在面内复习回顾 怎样判定直线与平面平行呢?依定义,需判定直线与平面无公共点.
[来源:学科网ZXXK]问题提出: 直线无限延长,平面无限延展.
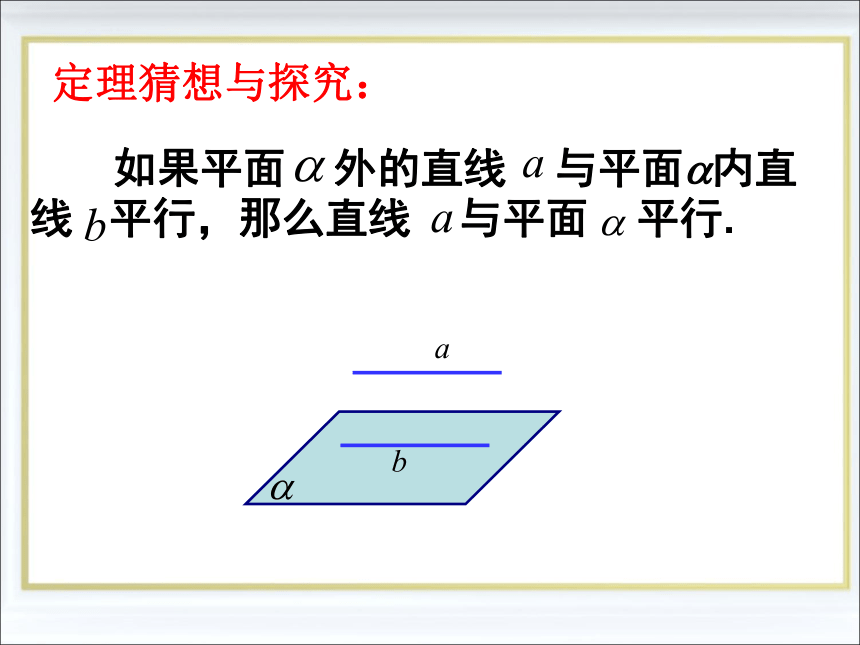
判断直线与平面没有公共点很难!想一想,猜一猜: 从中你能得出什么猜想?定理猜想与探究:(1)直线a与b共面吗?探究:共面不可能相交 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.直线与平面平行判定定理符号表示? 之前,我们学过哪些判定直线与直线平行
的方法?D1.下列说法正确的是( )定理的辨析与应用证明直线与平面平行,面外,面内,平行三个条件缺一不可 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
证明:EF//平面BCD.ABCDEF 分析:要证明线面平行只需证明线线平行,即在平面BCD内找一条直线 平行于EF,由已知的条件怎样找这条直线?变式1 如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 ,则EF
与平面BCD的位置关系是_____________.
EF//平面BCDABCDEFAEBDC如图,空间四边形ABCD中,E是AB上的一点,试过
CE作一平面平行于BD,说明画法.变式引申ABCDFOE变式2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点.
求证:AB//平面DCF.
(04年天津高考)分析:连接OF,可知OF为△ABE的中位线,所以得到AB//OF.∵ O为正方形DBCE 对角线的交点,
∴BO=OE,
又F为AE的中点,∴AB//OF,BDFO变式 2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF.证明:连接OF,ACE∴AB//平面DCF.
变式3:能否证明OF//面ABD?OF//面ABC吗?例2、如图所示四棱锥P-ABCD, 底面ABCD为矩形,M,N分别为AB,PC中点.
求证:MN//平面PAD分析:找一条在平面
PAD内并且和MN平行
的直线O证:取PD的中点O,
连接OA,ON∵N是PC的中点又M是矩形ABCD的
边AB的中点例2、如图所示四棱锥P-ABCD, 底面ABCD为矩形,M,N分别为AB,PC中点.
求证:MN//平面PADO∵ MN//平面PAD1.证明直线与平面平行的方法:(1)利用定义;(2)利用判定定理(注意:面外,面内,平行).2.数学思想方法:转化化归的思想直线与平面没有公共点小结 1、 如图,正方体ABCD-A1B1C1D1中,E,F,G分别为DD1,BC,C1D1的中点,
(1)求证:BD1//平面AEC;
(2)求证:FG//平面BDD1B1 O作业布置:
GF
———直线与平面平行的判定内容关系直线在平面内直线与平面
相交直线与平面
平行有无数个
公共点有且只有一个
公共点无公共点 直线与平面的位置关系有哪些?线不在面内复习回顾 怎样判定直线与平面平行呢?依定义,需判定直线与平面无公共点.
[来源:学科网ZXXK]问题提出: 直线无限延长,平面无限延展.
判断直线与平面没有公共点很难!想一想,猜一猜: 从中你能得出什么猜想?定理猜想与探究:(1)直线a与b共面吗?探究:共面不可能相交 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.直线与平面平行判定定理符号表示? 之前,我们学过哪些判定直线与直线平行
的方法?D1.下列说法正确的是( )定理的辨析与应用证明直线与平面平行,面外,面内,平行三个条件缺一不可 例1. 如图,空间四边形ABCD中,
E、F分别是 AB,AD的中点.
证明:EF//平面BCD.ABCDEF 分析:要证明线面平行只需证明线线平行,即在平面BCD内找一条直线 平行于EF,由已知的条件怎样找这条直线?变式1 如图,在空间四边形ABCD中,E、F分
别为AB、AD上的点,若 ,则EF
与平面BCD的位置关系是_____________.
EF//平面BCDABCDEFAEBDC如图,空间四边形ABCD中,E是AB上的一点,试过
CE作一平面平行于BD,说明画法.变式引申ABCDFOE变式2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点.
求证:AB//平面DCF.
(04年天津高考)分析:连接OF,可知OF为△ABE的中位线,所以得到AB//OF.∵ O为正方形DBCE 对角线的交点,
∴BO=OE,
又F为AE的中点,∴AB//OF,BDFO变式 2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF.证明:连接OF,ACE∴AB//平面DCF.
变式3:能否证明OF//面ABD?OF//面ABC吗?例2、如图所示四棱锥P-ABCD, 底面ABCD为矩形,M,N分别为AB,PC中点.
求证:MN//平面PAD分析:找一条在平面
PAD内并且和MN平行
的直线O证:取PD的中点O,
连接OA,ON∵N是PC的中点又M是矩形ABCD的
边AB的中点例2、如图所示四棱锥P-ABCD, 底面ABCD为矩形,M,N分别为AB,PC中点.
求证:MN//平面PADO∵ MN//平面PAD1.证明直线与平面平行的方法:(1)利用定义;(2)利用判定定理(注意:面外,面内,平行).2.数学思想方法:转化化归的思想直线与平面没有公共点小结 1、 如图,正方体ABCD-A1B1C1D1中,E,F,G分别为DD1,BC,C1D1的中点,
(1)求证:BD1//平面AEC;
(2)求证:FG//平面BDD1B1 O作业布置:
GF
