6.2垂直关系的性质 课件(20张PPT)
文档属性
| 名称 | 6.2垂直关系的性质 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 663.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 21:45:08 | ||
图片预览







文档简介
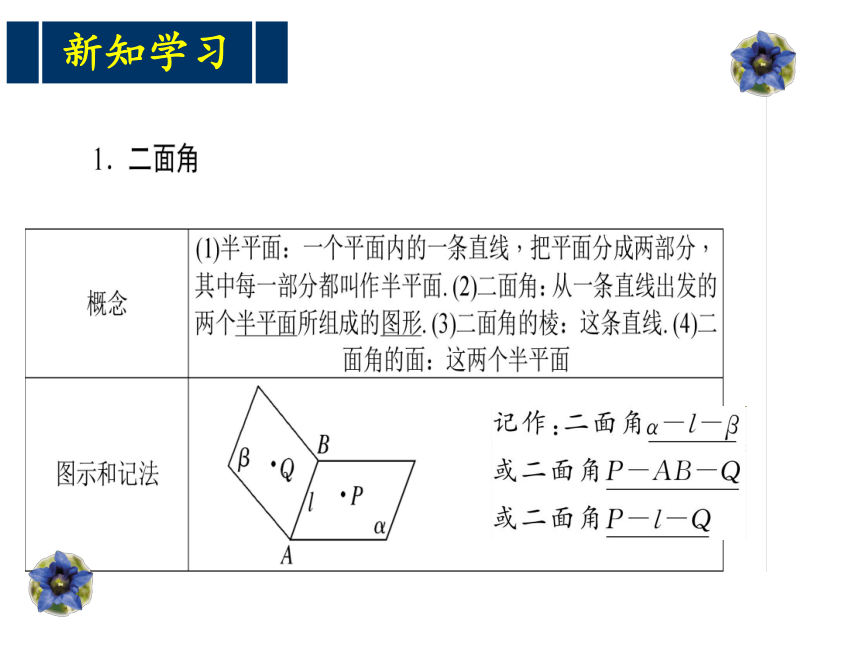
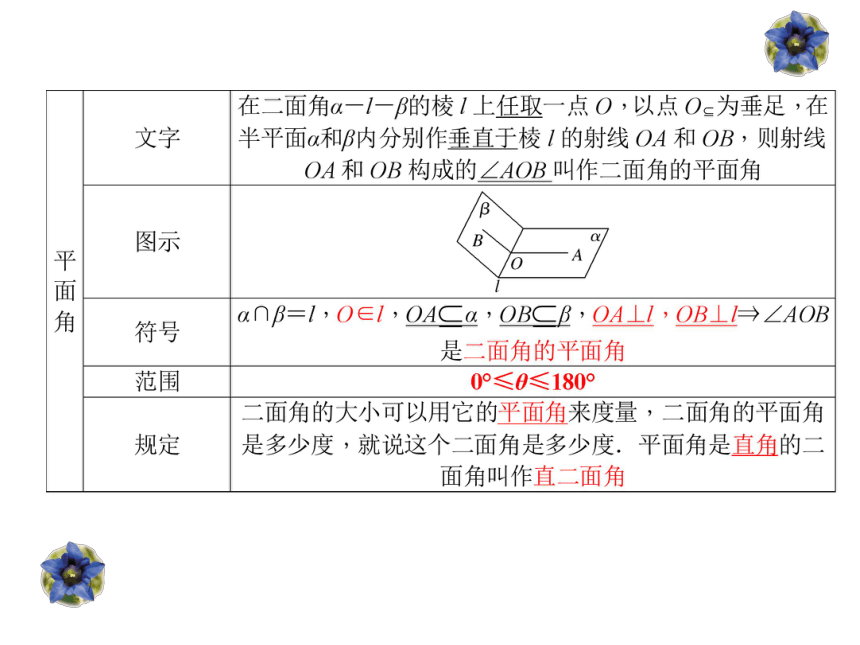
课件20张PPT。 余弦函数的图像学习目标1.描点法 平面与平面垂直的判定知识回顾线面垂直的判定及符号表示?联系实际预习检测4.面面垂直是如何定义的?1.二面角的定义是什么?3.怎样找二面角的平面角?2.二面角的范围是什么?新知学习互动讲练O思路点拨求二面角的步骤简称为“一作二证三求”新知学习面面垂直判定定理的探究 (1)动手实践:将一支铅笔垂直于桌面,再 用一本书紧贴着铅笔转动,观察书与桌面的位置关系。你发现了什么?(2)能把你发现的结论用数学语言表示出来吗?交流探讨(3)能证明这个结论吗?抽象概括面面垂直的判定 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。图形语言:l⊥α,l符号语言: β ?α⊥β线面垂直?面面垂直互动讲练类型一 平面与平面垂直的证明[例1] 如图,已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=SB=SC=2,求证:平面ABC⊥平面SBC.O互动讲练例2.如图所示, AB为⊙O的直径, ⊙O所在平面为α. PA⊥于A, C为⊙O上异于A, B的一点. 求证:平面PAC⊥平面PBC.规律方法证明面面垂直的方法 根据面面垂直的定义判定两平面垂直,实质上是把问题转化成了求二面角的平面角,通常情况下利用判定定理要比定义简单些,判定定理是证明面面垂直的常用方法。(1)二面角的平面角是从二面角的棱上一点出发,分别在两个面内作射线所成的最小角.( )
(2)二面角的大小与其平面角的顶点在二面角的棱上的位置没有关系.( )
(3)若平面α和平面β分别过两条互相垂直的直线,则α⊥β.( )
(4)若平面α内的一条直线垂直于平面β内的两条平行直线, 则α⊥β( )自我检测自我检测1.在空间四边形ABCD中,AB=BC,AD=CD,E为对角线AC的中点,下列判断正确的是( )
A.平面ABD⊥平面BDC
B.平面ABC⊥平面ABD
C.平面ABC⊥平面ADC
D.平面ABC⊥平面BED3.
2.如图所示,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,则二面角B-PA-C的大小为( )
A.90°B.60°
C.45°D.30°
自我检测3.如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥DC,DC⊥AC.(1)求证:DC⊥平面PAC;
(2)求证:平面PAB⊥平面PAC.
谈谈你本节课的收获 1.正式作业:
本节练习3,4
习题1-6A组第6题(2)(3)2.练习作业:
完成大册子习题1,2,3,4
(2)二面角的大小与其平面角的顶点在二面角的棱上的位置没有关系.( )
(3)若平面α和平面β分别过两条互相垂直的直线,则α⊥β.( )
(4)若平面α内的一条直线垂直于平面β内的两条平行直线, 则α⊥β( )自我检测自我检测1.在空间四边形ABCD中,AB=BC,AD=CD,E为对角线AC的中点,下列判断正确的是( )
A.平面ABD⊥平面BDC
B.平面ABC⊥平面ABD
C.平面ABC⊥平面ADC
D.平面ABC⊥平面BED3.
2.如图所示,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,则二面角B-PA-C的大小为( )
A.90°B.60°
C.45°D.30°
自我检测3.如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥DC,DC⊥AC.(1)求证:DC⊥平面PAC;
(2)求证:平面PAB⊥平面PAC.
谈谈你本节课的收获 1.正式作业:
本节练习3,4
习题1-6A组第6题(2)(3)2.练习作业:
完成大册子习题1,2,3,4
