北师大版 必修2 第一章立体几何初步 习题1-4 课件(24张PPT)
文档属性
| 名称 | 北师大版 必修2 第一章立体几何初步 习题1-4 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 414.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览





文档简介
课件24张PPT。
心中有物 , 眼中有图
高中数学北师大版必修2
第一章 立体几何初步
1.4 空间图形基本关系与公理
习题1.4
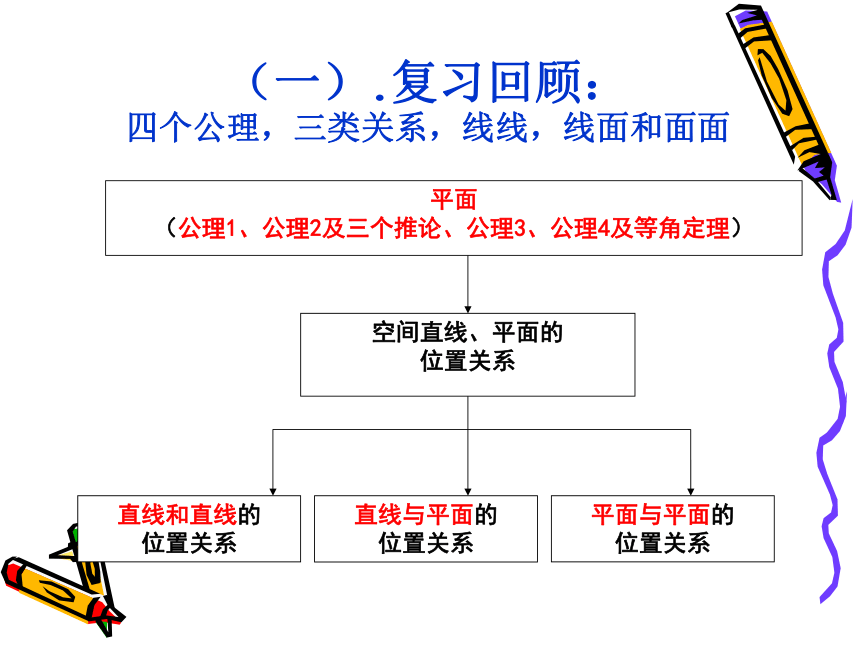
(一).复习回顾: 四个公理,三类关系,线线,线面和面面1.平面公理1. 如果一条直线上的两点在一个平面内,那么这条直线在这个平面内.
符号表示:
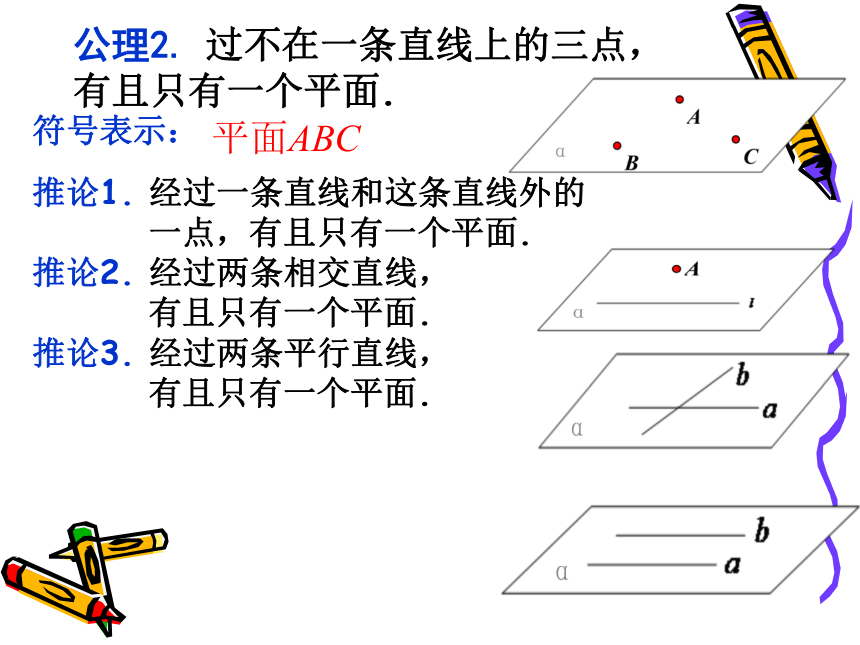
注:线入面,需两点.公理2. 过不在一条直线上的三点,有且只有一个平面.符号表示:
推论1. 经过一条直线和这条直线外的
一点,有且只有一个平面.
推论2. 经过两条相交直线,
有且只有一个平面.
推论3. 经过两条平行直线,
有且只有一个平面.
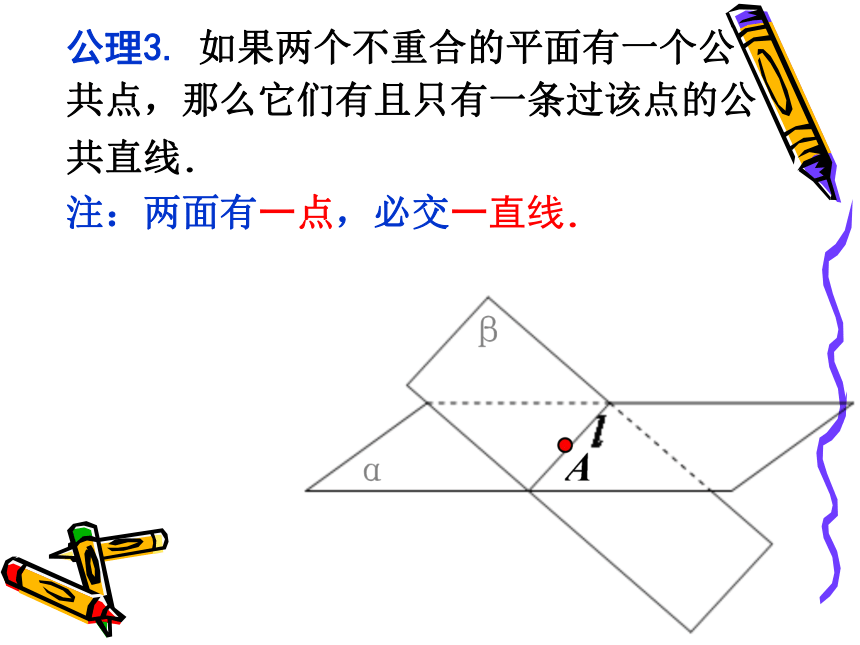
公理3. 如果两个不重合的平面有一个公
共点,那么它们有且只有一条过该点的公
共直线.
注:两面有一点,必交一直线.
公理4. 平行于同一条直线的两条直线互相平行.(平行线的传递性)
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.(等角定理)
2.空间点、直线、平面之间的位置关系(线线,线面和面面)
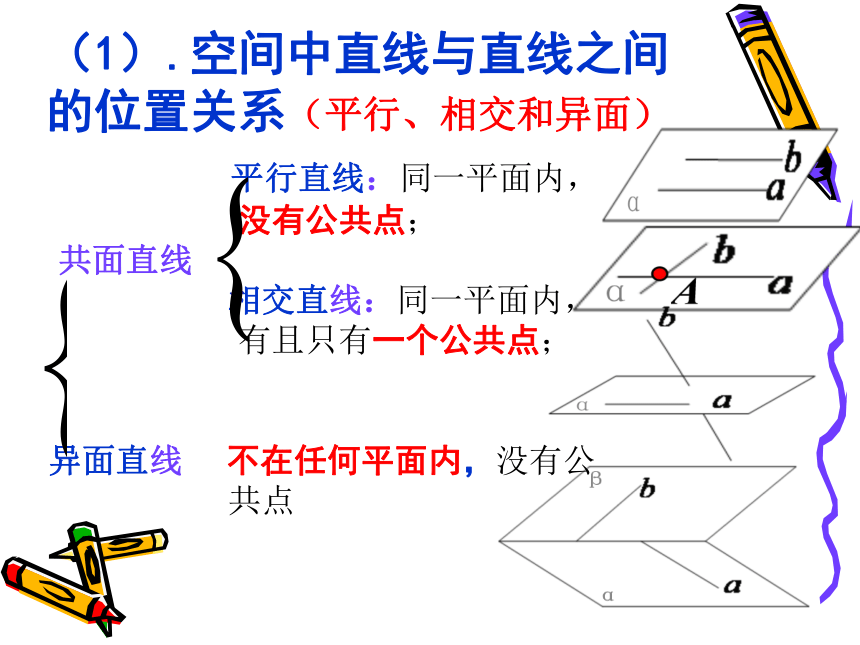
(1).空间中直线与直线之间的位置关系(平行、相交和异面) 平行直线:同一平面内,
没有公共点;
共面直线
相交直线:同一平面内,
有且只有一个公共点;
异面直线 不在任何平面内,没有公
共点(2).空间直线与平面之间的位置关系(相交、平行和面内) 直线在平面内:有无数个公共点,
符号表示: ;
直线与平面相交:有且只有一个
公共点,符号表示: ;
直线与平面平行:没有公共点,
符号表示: .(3).平面与平面之间的位置关系:平行与相交 两个平面平行:没有公共点,
符号表示: ;
两个平面相交:有一条公共直
线,符号表示: ;例1.填空:
(1).已知 , , 是三条直线, ∥ ,
与 的夹角为 ,那么 与 的夹
角为 . 能力提升1.会辨 实物助直观(2).已知两条相交直线 , ,
∥ ,则 与 的关系是 .平行或相交(3).设直线 , 分别是长方体相邻两个面的对角线,则 与 的位置关系是 .相交直线或异面直线能力提升2.会求异面直线夹角:平移至相交,空间化平面.
解题步骤:1.作图 2.证明 3.计算例2 .如图,正方体 中,正方体的棱长为2,求下列异面直线的夹角的余弦值.
(1) 和 ;
例2 .如图,正方体 中,正方体的棱长为2,求下列异面直线的夹角的余弦值.
(1) 和 ;
解:连接 和 ,因为 ,
,所以 ∥ ,
所以 和 的夹角
即为 和 的夹角.
因为 ,
所以 是正三角形,
所以 和 的夹角
为的 余弦值为 .
例2 .如图,正方体 中,正方体的棱长为2.求下列异面直线的夹角的余弦值.
(2) 和 .
例2 .如图,正方体 中,正方体的棱长为2.求下列异面直线的夹角的余弦值.
(2) 和 .
法一:
例2 .如图,正方体 中,正方体的棱长为2.求下列异面直线的夹角的余弦值.
(2) 和 .
法二:
例2 .如图,正方体 中,
正方体的棱长为2.求下列异面直线的夹角的余弦值.
(2) 和 .
法三:
练习.如图,正方体 中,
的中点为 , 的中点为 ,则
异面直线 与 所成的角是( ).
(A)0°
(B)45°
(C)60°
(D)90°练习.如图,正方体 中,
的中点为 , 的中点为 ,则
异面直线 与 所成的角是( ).
(A)0°
(B)45°
(C)60°
(D)90°D 课堂小结心中有物,眼中有图,实物助直观
会辨:动静结合,平转皆有,条件不变,关系思全;
会求:异面直线夹角,平移至相交,空间化平面;
作业
必做题 :
习题1. 4 A组1,2,,5 B组1,2
选做题:已知三棱锥 的棱长均为2 ,求棱 与 的夹角.
第一章 立体几何初步
1.4 空间图形基本关系与公理
习题1.4
(一).复习回顾: 四个公理,三类关系,线线,线面和面面1.平面公理1. 如果一条直线上的两点在一个平面内,那么这条直线在这个平面内.
符号表示:
注:线入面,需两点.公理2. 过不在一条直线上的三点,有且只有一个平面.符号表示:
推论1. 经过一条直线和这条直线外的
一点,有且只有一个平面.
推论2. 经过两条相交直线,
有且只有一个平面.
推论3. 经过两条平行直线,
有且只有一个平面.
公理3. 如果两个不重合的平面有一个公
共点,那么它们有且只有一条过该点的公
共直线.
注:两面有一点,必交一直线.
公理4. 平行于同一条直线的两条直线互相平行.(平行线的传递性)
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.(等角定理)
2.空间点、直线、平面之间的位置关系(线线,线面和面面)
(1).空间中直线与直线之间的位置关系(平行、相交和异面) 平行直线:同一平面内,
没有公共点;
共面直线
相交直线:同一平面内,
有且只有一个公共点;
异面直线 不在任何平面内,没有公
共点(2).空间直线与平面之间的位置关系(相交、平行和面内) 直线在平面内:有无数个公共点,
符号表示: ;
直线与平面相交:有且只有一个
公共点,符号表示: ;
直线与平面平行:没有公共点,
符号表示: .(3).平面与平面之间的位置关系:平行与相交 两个平面平行:没有公共点,
符号表示: ;
两个平面相交:有一条公共直
线,符号表示: ;例1.填空:
(1).已知 , , 是三条直线, ∥ ,
与 的夹角为 ,那么 与 的夹
角为 . 能力提升1.会辨 实物助直观(2).已知两条相交直线 , ,
∥ ,则 与 的关系是 .平行或相交(3).设直线 , 分别是长方体相邻两个面的对角线,则 与 的位置关系是 .相交直线或异面直线能力提升2.会求异面直线夹角:平移至相交,空间化平面.
解题步骤:1.作图 2.证明 3.计算例2 .如图,正方体 中,正方体的棱长为2,求下列异面直线的夹角的余弦值.
(1) 和 ;
例2 .如图,正方体 中,正方体的棱长为2,求下列异面直线的夹角的余弦值.
(1) 和 ;
解:连接 和 ,因为 ,
,所以 ∥ ,
所以 和 的夹角
即为 和 的夹角.
因为 ,
所以 是正三角形,
所以 和 的夹角
为的 余弦值为 .
例2 .如图,正方体 中,正方体的棱长为2.求下列异面直线的夹角的余弦值.
(2) 和 .
例2 .如图,正方体 中,正方体的棱长为2.求下列异面直线的夹角的余弦值.
(2) 和 .
法一:
例2 .如图,正方体 中,正方体的棱长为2.求下列异面直线的夹角的余弦值.
(2) 和 .
法二:
例2 .如图,正方体 中,
正方体的棱长为2.求下列异面直线的夹角的余弦值.
(2) 和 .
法三:
练习.如图,正方体 中,
的中点为 , 的中点为 ,则
异面直线 与 所成的角是( ).
(A)0°
(B)45°
(C)60°
(D)90°练习.如图,正方体 中,
的中点为 , 的中点为 ,则
异面直线 与 所成的角是( ).
(A)0°
(B)45°
(C)60°
(D)90°D 课堂小结心中有物,眼中有图,实物助直观
会辨:动静结合,平转皆有,条件不变,关系思全;
会求:异面直线夹角,平移至相交,空间化平面;
作业
必做题 :
习题1. 4 A组1,2,,5 B组1,2
选做题:已知三棱锥 的棱长均为2 ,求棱 与 的夹角.
