1.1直线的倾斜角和斜率 课件(21张PPT)
文档属性
| 名称 | 1.1直线的倾斜角和斜率 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 782.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览






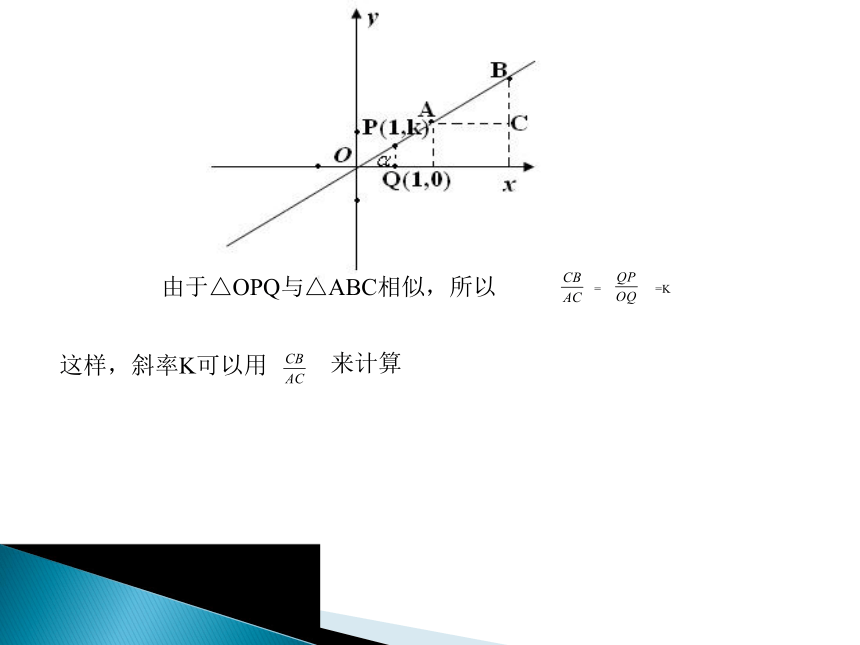
文档简介
课件21张PPT。1.1 直线的倾斜角和斜率高一数学一.回顾旧知 1.点的确定
在平面直角坐标系中,用什么条件可以确定一个点呢?2.直线的确定 在平面直角坐标系中,怎样刻画一条位置确定的直线呢?抽象概括
在平面直角坐标系中,确定直线位置的几何条件是:已知直线上的一个点和这条直线的方向.二.新知探究
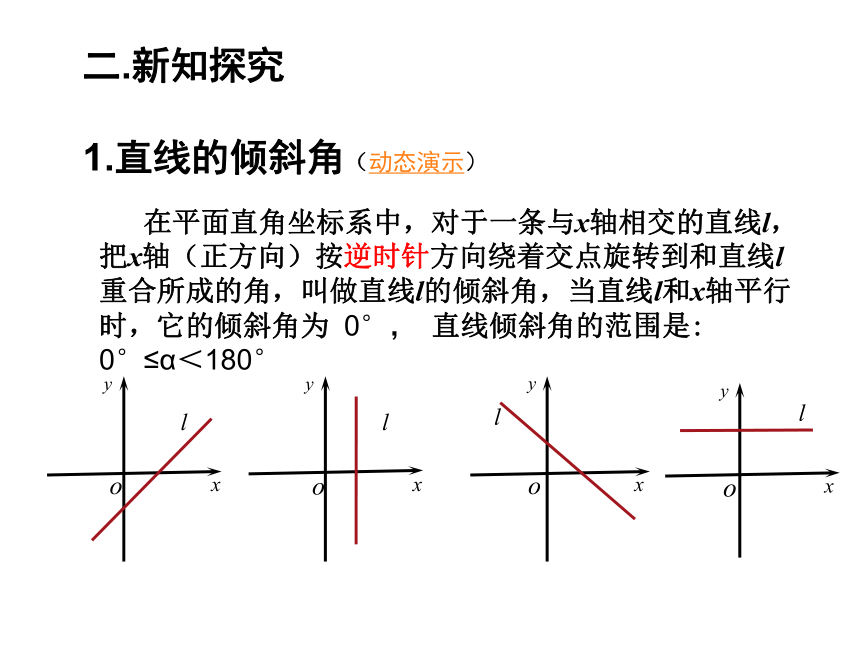
1.直线的倾斜角(动态演示)
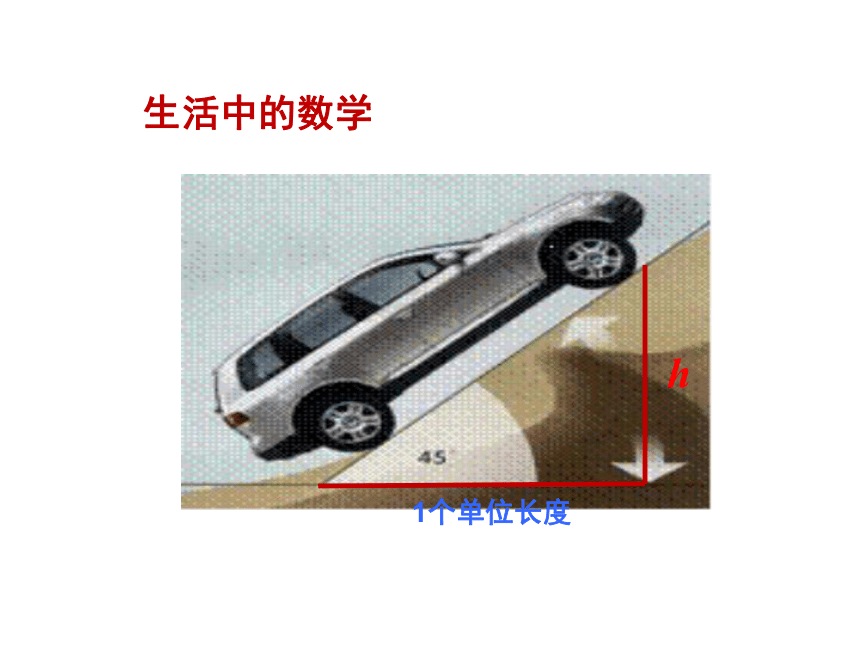
在平面直角坐标系中,对于一条与x轴相交的直线l,把x轴(正方向)按逆时针方向绕着交点旋转到和直线l重合所成的角,叫做直线l的倾斜角,当直线l和x轴平行时,它的倾斜角为 0°, 直线倾斜角的范围是: 0°≤α<180°1个单位长度h生活中的数学 由于△OPQ与△ABC相似,所以==K 这样,斜率K可以用来计算 思考:
1.对于倾斜角是90° 的直线,它的斜率是多少?2.不通过坐标原点的直线,它的斜率如何定义呢?倾斜角与斜率的对应关系α=0°0°<α<90°α=90°90°<α<180°k=0k>0斜率不存在k<0【提升总结】思考:当倾斜角 变化时,斜率如何变化? 经过平面内不同的两点P(x1 , y1),Q(x2 , y2)
的直线的斜率:
3.过两点的直线的斜率公式 判断下列说法是否正确:
(1)任何一条直线都有唯一的倾斜角;
(2)任何一条直线都有唯一的斜率;
(3)直线的倾斜角越大斜率也越大. 三.典例解析 例1你学会了吗? 例2如图,已知直线l1,l2,l3的斜率分别是k1,k2,k3,
试比较k1,k2,k3的大小例3求过已知两点的直线的斜率并指出其
倾斜角是锐角、直角还是钝角:
(1)直线PQ过点P(2,3),Q(6,5);
(2)直线AB过点A(-3,5),B(4,-2)
(3)直线CD过点C(1,-2),B(5,-2)
(4)直线EF过点E(3,0),B(3,-2)。
已知直角坐标平面内三点A(3,2),B(-2,1), C(m,- 1).
(1) 求直线AB的斜率;
(2) 求直线AC的斜率;
(3)若A,B,C三点共线,求m的值. (2)∵A,B,C 三点共线四.变式练习五.课堂小结1.确定直线位置的几何条件;
2.直线的倾斜角定义及其范围;
3.直线的斜率.定点
方向直线倾斜角斜率六.作业课后习题A组1、2题;预习直线的点斜式方程.谢谢大家!
在平面直角坐标系中,用什么条件可以确定一个点呢?2.直线的确定 在平面直角坐标系中,怎样刻画一条位置确定的直线呢?抽象概括
在平面直角坐标系中,确定直线位置的几何条件是:已知直线上的一个点和这条直线的方向.二.新知探究
1.直线的倾斜角(动态演示)
在平面直角坐标系中,对于一条与x轴相交的直线l,把x轴(正方向)按逆时针方向绕着交点旋转到和直线l重合所成的角,叫做直线l的倾斜角,当直线l和x轴平行时,它的倾斜角为 0°, 直线倾斜角的范围是: 0°≤α<180°1个单位长度h生活中的数学 由于△OPQ与△ABC相似,所以==K 这样,斜率K可以用来计算 思考:
1.对于倾斜角是90° 的直线,它的斜率是多少?2.不通过坐标原点的直线,它的斜率如何定义呢?倾斜角与斜率的对应关系α=0°0°<α<90°α=90°90°<α<180°k=0k>0斜率不存在k<0【提升总结】思考:当倾斜角 变化时,斜率如何变化? 经过平面内不同的两点P(x1 , y1),Q(x2 , y2)
的直线的斜率:
3.过两点的直线的斜率公式 判断下列说法是否正确:
(1)任何一条直线都有唯一的倾斜角;
(2)任何一条直线都有唯一的斜率;
(3)直线的倾斜角越大斜率也越大. 三.典例解析 例1你学会了吗? 例2如图,已知直线l1,l2,l3的斜率分别是k1,k2,k3,
试比较k1,k2,k3的大小例3求过已知两点的直线的斜率并指出其
倾斜角是锐角、直角还是钝角:
(1)直线PQ过点P(2,3),Q(6,5);
(2)直线AB过点A(-3,5),B(4,-2)
(3)直线CD过点C(1,-2),B(5,-2)
(4)直线EF过点E(3,0),B(3,-2)。
已知直角坐标平面内三点A(3,2),B(-2,1), C(m,- 1).
(1) 求直线AB的斜率;
(2) 求直线AC的斜率;
(3)若A,B,C三点共线,求m的值. (2)∵A,B,C 三点共线四.变式练习五.课堂小结1.确定直线位置的几何条件;
2.直线的倾斜角定义及其范围;
3.直线的斜率.定点
方向直线倾斜角斜率六.作业课后习题A组1、2题;预习直线的点斜式方程.谢谢大家!
