1.3两条直线的位置关系 课件(23张PPT)
文档属性
| 名称 | 1.3两条直线的位置关系 课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 21:55:07 | ||
图片预览








文档简介
课件23张PPT。问题2:过原点且与x轴正方向所成的角
为30o的直线有多少条?问题1:倾斜角为30o的直线有多少条?有无数条O问题引入观察这几条直线具有怎样的位置关系?一条过原点且与x轴正方向所成的角为120o的直线有多少条?互相平行(重合)
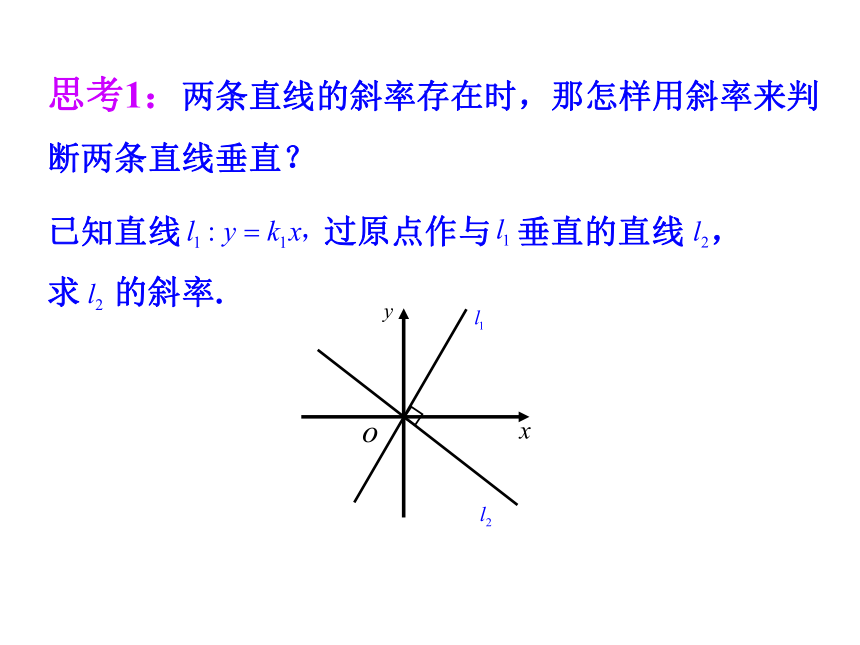
一条问题3:观察问题2中的两条直线具有怎样的位置关系?垂直在平面直角坐标系中,怎样根据直线方程的特征(斜率)判断两条直线方程的位置关系呢?平行垂直重合思考:通过上面的实例总结出平面内两直线的位置关 系有哪些?1.3 两条直线的位置关系 我们可以知道,斜率相等的两条直线探究点1 两条直线平行相等.它们相互平行(重合);反之,两条直线平行,它们的倾斜角相等,若倾斜角不为90°,则它们的斜率相等. α2倾斜角斜率不存在时两直线的平行当两条直线中有一条直线 没有斜率时, 那另一条直线 的斜率应该满足什么条件?? 如果两直线位置关系为:互相平行斜率不存在,倾斜角为90° l1l2斜率存在时两直线的平行:两条直线 和 ,另一条直线的斜率为 0如果,两直线位置关系为:互相垂直.探究点2 两条直线垂直当两条直线中有一条直线没有斜率时, 那另一条直线的斜率应该满足什么条件?? 思考1:两条直线的斜率存在时,那怎样用斜率来判断两条直线垂直?解:设直线 的直线方程为:那 的方向向量为: 的方向向量为:解法一:为O解法二:思考2:当直线的斜率不存在时, l1⊥l2?k1k2=-1
还适用吗? 当直线的斜率不存在时上述公式不适用,
此时直线的倾斜角是90°,斜率不存在。例1 判断下列各对直线是否平行还是垂直,并说明理由:例题讲解 解:设两直线的斜率分别是 , ,在y轴上截距
分别是 , ,则 因为 所以 . (2)(1)解:设两直线的斜率分别是 则
有 所以(3)解: 设两直线的斜率分别是 则
有 所以(4)(5)解:由方程可知, 轴, 轴,且两直线在 轴上截距
不相等,所以 .思考3:能否根据直线方程的一般式来判断两
直线的位置关系呢??(1)与平行则垂直与(2)例2 求过点 且平行于直线 的直线方程. 解:所求直线平行于直线 ,所以它们
的斜率相等,都为
而所求直线过
所以,所求直线的方程为 ,
即 .解:已知直线 的斜率为 ,所求直线与已知直线垂直,所以该直线的斜率为 ,
且该直线过点 ,
因此所求直线方程为 ,
即例3 求过点 且垂直于直线 的直线方程.1.已知不重合的两条直线 ,下列说法中正确的是_____.
①若直线 与 的斜率相等,则 ;
②若直线 ,则两直线的斜率相等;
③若直线 的斜率不相等,则两直线不平行;
④若直线 的斜率均不存在,则 ;
⑤如果直线 平行,且 的斜率不存在,那么 的斜率也不存在.①③④⑤②中斜率可能不存在,①③④⑤正确。2.直线x+ay-7=0与直线(a+1)x+2y-14=0互相平行, 则a的值是( ) A.1 B.-2 C.1或-2 D.-1或2 B3.若直线x+ay+1=0与直线(a+1)x-2y+3=0互相垂直,则实数a=_______.14.已知直线 l满足下列条件,求直线l的方程.
(1)经过点A(3,2)且与直线4x+y-2=0平行;
(2)经过点B(3,0)且与直线2x+y-5=0垂直.解: (1)所求直线平行于直线 ,所以它们的斜率相等,都为 而所求直线过
所求直线的方程为 ,即 .解:(2)已知直线 的斜率为 ,所求直线
与已知直线垂直,所以该直线的斜率为 ,且该直线过点 ,因此所求直线方程为 ,
即斜率间的关系(若l1,l2的斜率都存在,设l1:y=k1x+b1, l2:y=k2x+b2)l1∥l2?k1=k2,且b1≠b2l1⊥l2? k1?k2= -1 (1)与平行垂直与(2)直线方程的一般式来判断两直线的位置关系:作业1.预习导学案: 的对称问题2.完成固学案: 的练习3.将导学案: 的变式训练1和固学案: 预习检测第3题写在作业本上。
为30o的直线有多少条?问题1:倾斜角为30o的直线有多少条?有无数条O问题引入观察这几条直线具有怎样的位置关系?一条过原点且与x轴正方向所成的角为120o的直线有多少条?互相平行(重合)
一条问题3:观察问题2中的两条直线具有怎样的位置关系?垂直在平面直角坐标系中,怎样根据直线方程的特征(斜率)判断两条直线方程的位置关系呢?平行垂直重合思考:通过上面的实例总结出平面内两直线的位置关 系有哪些?1.3 两条直线的位置关系 我们可以知道,斜率相等的两条直线探究点1 两条直线平行相等.它们相互平行(重合);反之,两条直线平行,它们的倾斜角相等,若倾斜角不为90°,则它们的斜率相等. α2倾斜角斜率不存在时两直线的平行当两条直线中有一条直线 没有斜率时, 那另一条直线 的斜率应该满足什么条件?? 如果两直线位置关系为:互相平行斜率不存在,倾斜角为90° l1l2斜率存在时两直线的平行:两条直线 和 ,另一条直线的斜率为 0如果,两直线位置关系为:互相垂直.探究点2 两条直线垂直当两条直线中有一条直线没有斜率时, 那另一条直线的斜率应该满足什么条件?? 思考1:两条直线的斜率存在时,那怎样用斜率来判断两条直线垂直?解:设直线 的直线方程为:那 的方向向量为: 的方向向量为:解法一:为O解法二:思考2:当直线的斜率不存在时, l1⊥l2?k1k2=-1
还适用吗? 当直线的斜率不存在时上述公式不适用,
此时直线的倾斜角是90°,斜率不存在。例1 判断下列各对直线是否平行还是垂直,并说明理由:例题讲解 解:设两直线的斜率分别是 , ,在y轴上截距
分别是 , ,则 因为 所以 . (2)(1)解:设两直线的斜率分别是 则
有 所以(3)解: 设两直线的斜率分别是 则
有 所以(4)(5)解:由方程可知, 轴, 轴,且两直线在 轴上截距
不相等,所以 .思考3:能否根据直线方程的一般式来判断两
直线的位置关系呢??(1)与平行则垂直与(2)例2 求过点 且平行于直线 的直线方程. 解:所求直线平行于直线 ,所以它们
的斜率相等,都为
而所求直线过
所以,所求直线的方程为 ,
即 .解:已知直线 的斜率为 ,所求直线与已知直线垂直,所以该直线的斜率为 ,
且该直线过点 ,
因此所求直线方程为 ,
即例3 求过点 且垂直于直线 的直线方程.1.已知不重合的两条直线 ,下列说法中正确的是_____.
①若直线 与 的斜率相等,则 ;
②若直线 ,则两直线的斜率相等;
③若直线 的斜率不相等,则两直线不平行;
④若直线 的斜率均不存在,则 ;
⑤如果直线 平行,且 的斜率不存在,那么 的斜率也不存在.①③④⑤②中斜率可能不存在,①③④⑤正确。2.直线x+ay-7=0与直线(a+1)x+2y-14=0互相平行, 则a的值是( ) A.1 B.-2 C.1或-2 D.-1或2 B3.若直线x+ay+1=0与直线(a+1)x-2y+3=0互相垂直,则实数a=_______.14.已知直线 l满足下列条件,求直线l的方程.
(1)经过点A(3,2)且与直线4x+y-2=0平行;
(2)经过点B(3,0)且与直线2x+y-5=0垂直.解: (1)所求直线平行于直线 ,所以它们的斜率相等,都为 而所求直线过
所求直线的方程为 ,即 .解:(2)已知直线 的斜率为 ,所求直线
与已知直线垂直,所以该直线的斜率为 ,且该直线过点 ,因此所求直线方程为 ,
即斜率间的关系(若l1,l2的斜率都存在,设l1:y=k1x+b1, l2:y=k2x+b2)l1∥l2?k1=k2,且b1≠b2l1⊥l2? k1?k2= -1 (1)与平行垂直与(2)直线方程的一般式来判断两直线的位置关系:作业1.预习导学案: 的对称问题2.完成固学案: 的练习3.将导学案: 的变式训练1和固学案: 预习检测第3题写在作业本上。
