北师大版九年级数学上册第三章概率的进一步认识单元测试题(有详细答案)
文档属性
| 名称 | 北师大版九年级数学上册第三章概率的进一步认识单元测试题(有详细答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 348.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-21 00:00:00 | ||
图片预览



文档简介
北师大版九年级数学上册 第三章 概率的进一步认识 单元测试题
一.选择题(共10小题,每小题3分,共30分)
1.下列说法正确的是( )
A.为了解一批灯泡的使用寿命,宜采用普查方式
B.掷两枚质地均匀的硬币,两枚硬币都是正面朝上这一事件发生的概率为
C.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
D.甲乙两人在相同条件下各射击10次,他们成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
2.“学雷锋”活动月中,“飞翼”班将组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )
A. B. C. D.
3.如图,4×2的正方形网格中,在A,B,C,D四个点中任选三个点,能够组成等腰三角形的概率为( )
A.0 B. C. D.
4.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.若一次性摸出两个球,则一次性取出的两个小球标号的和不小于4的概率是( )
A. B. C. D.
5.消费者在网店购物后,将从“好评、中评、差评”中选择一种作为对卖家的评价,假设这三种评价是等可能的,若小明、小亮在某网店购买了同一商品,且都给出了评价,则两人中至少有一个给“好评”的概率为( )
A. B. C. D.
6.将一枚均匀的硬币连续抛掷两次,则两次都是正面朝上的概率等于( )
A.0.5 B.0.25 C.0.75 D.1
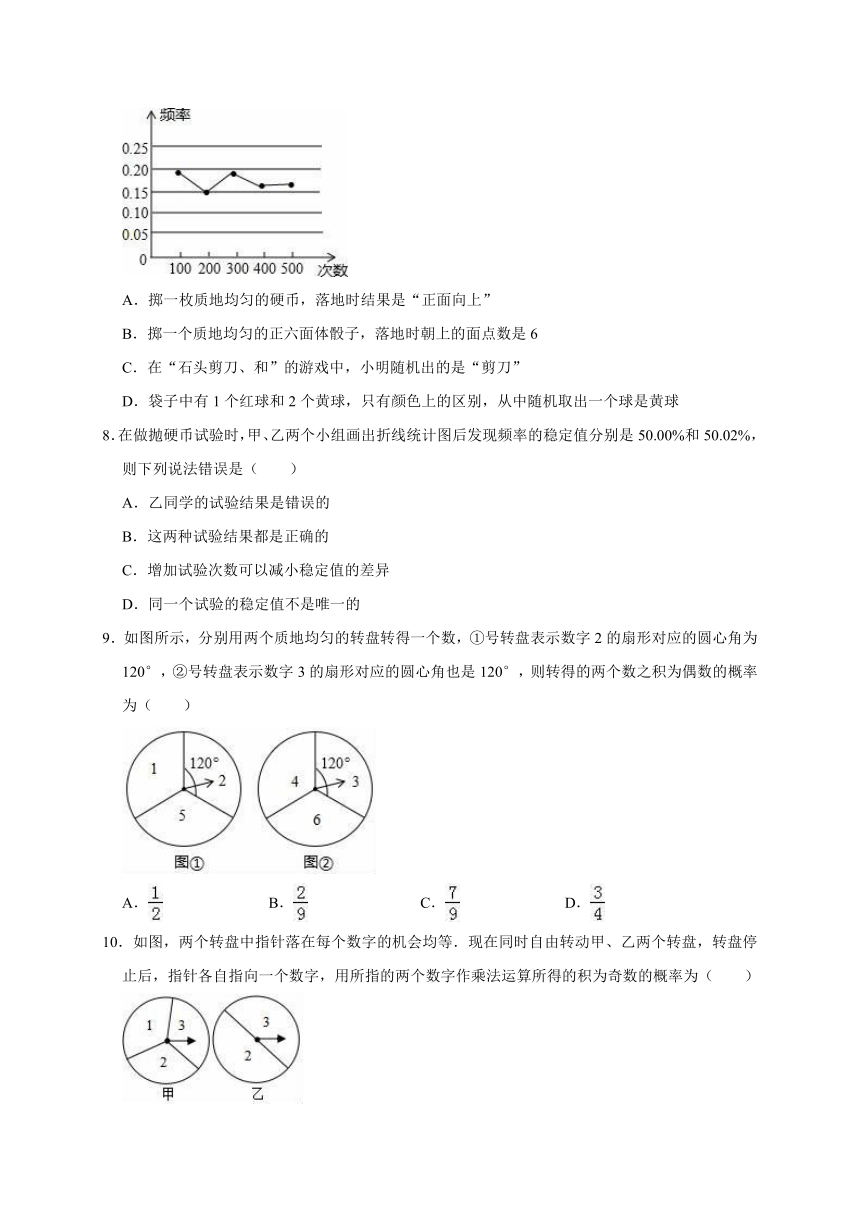
7.某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )
A.掷一枚质地均匀的硬币,落地时结果是“正面向上”
B.掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C.在“石头剪刀、和”的游戏中,小明随机出的是“剪刀”
D.袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
8.在做抛硬币试验时,甲、乙两个小组画出折线统计图后发现频率的稳定值分别是50.00%和50.02%,则下列说法错误是( )
A.乙同学的试验结果是错误的
B.这两种试验结果都是正确的
C.增加试验次数可以减小稳定值的差异
D.同一个试验的稳定值不是唯一的
9.如图所示,分别用两个质地均匀的转盘转得一个数,①号转盘表示数字2的扇形对应的圆心角为120°,②号转盘表示数字3的扇形对应的圆心角也是120°,则转得的两个数之积为偶数的概率为( )
A. B. C. D.
10.如图,两个转盘中指针落在每个数字的机会均等.现在同时自由转动甲、乙两个转盘,转盘停止后,指针各自指向一个数字,用所指的两个数字作乘法运算所得的积为奇数的概率为( )
A. B. C. D.
二.填空题(共8小题,每小题3分,共24分)
11.一个口袋中装有6个红球和4个白球,这些球除颜色外完全相同,充分搅匀后随机摸出一球发现是白球,如果这个白球不放回,再摸出一球,它是白球的概率是 .
12.一枚材质均匀的骰子,六个面的点数分别是1,2,3,4,5,6,投这个骰子,掷的点数大于4的概率是 .
13.从分别写有﹣1,﹣2,1,2的四张卡片中随机抽取两张,把第一张卡片上的数字作为a,第二张卡片上的数字作为b,则a,b之和大于0的概率是 .
14.在一个不透明的箱子里有四张外形相同的卡片?卡片上分别标有数字﹣1,1,3,5.摸出一张后,记下数字,再放回,摇匀后再摸出一张,记下数字.以第一次得到的放字为横坐标,第二次得到的数字为纵坐标,得到一个点则这个点.恰好在直线y=﹣x+4上的概率是 .
15.在两个暗盒中,各自装有编号为1,2,3的三个球,球除编号外无其它区别,则在两个暗盒中各取一个球,两球上的编号的积为偶数的概率为 .
16.某校春季运动会,小红参加100米和200米的比赛,每组六人分别在1﹣﹣6号跑道同时进行比赛,问小红两次都抽到3号跑道的概率是 .
17.在一个不透明的袋子中装有3个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.7附近,则袋子中红球约有 个.
18.如图,一个转盘的盘面被等分成四个扇形区域,并分别标有数字﹣1、0、1、2若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字的和等于0的概率为 .
三.解答题(共7小题,共66分)
19.“五一”期间,某商场推出“购物满额即可抽奖”活动.商场在抽奖箱中装有1个红球、2个黄球、3个白球、8个黑球,每个球除颜色外都相同,红球、黄球、白球分别代表一、二、三等奖,黑球代表谢谢参与.获得抽奖杋会的顾客每次从箱子中摸出一个球,按相应颜色对应等级兑换奖品,每次所摸得球再放回抽奖箱,摇匀后由下一位顾客抽奖.已知小明获得1次抽奖机会.
(1)小明是否一定能中奖: ;(填是、否)
(2)求出小明抽到一等奖的概率;
(3)在这个活动中,中奖和没中奖的机会相等吗?为什么?如果不相等,可以如何改变球的个数,使中奖和没中奖的机会相等?(只写一种即可)
20.如图,把一个转盘分成六等份,依次标上数字1、2、3、4、5、6,小明和小芳分别只转动一次转盘,小明同学先转动转盘,结果指针指向2,接下来小芳转动转盘、若把小明和小芳转动转盘指针指向的数字分别记作x、y,把x、y作为点A的横、纵坐标.
(1)写出点A(x,y)所有可能的坐标;
(2)求点A(x,y)在直线y=x+1上的概率.
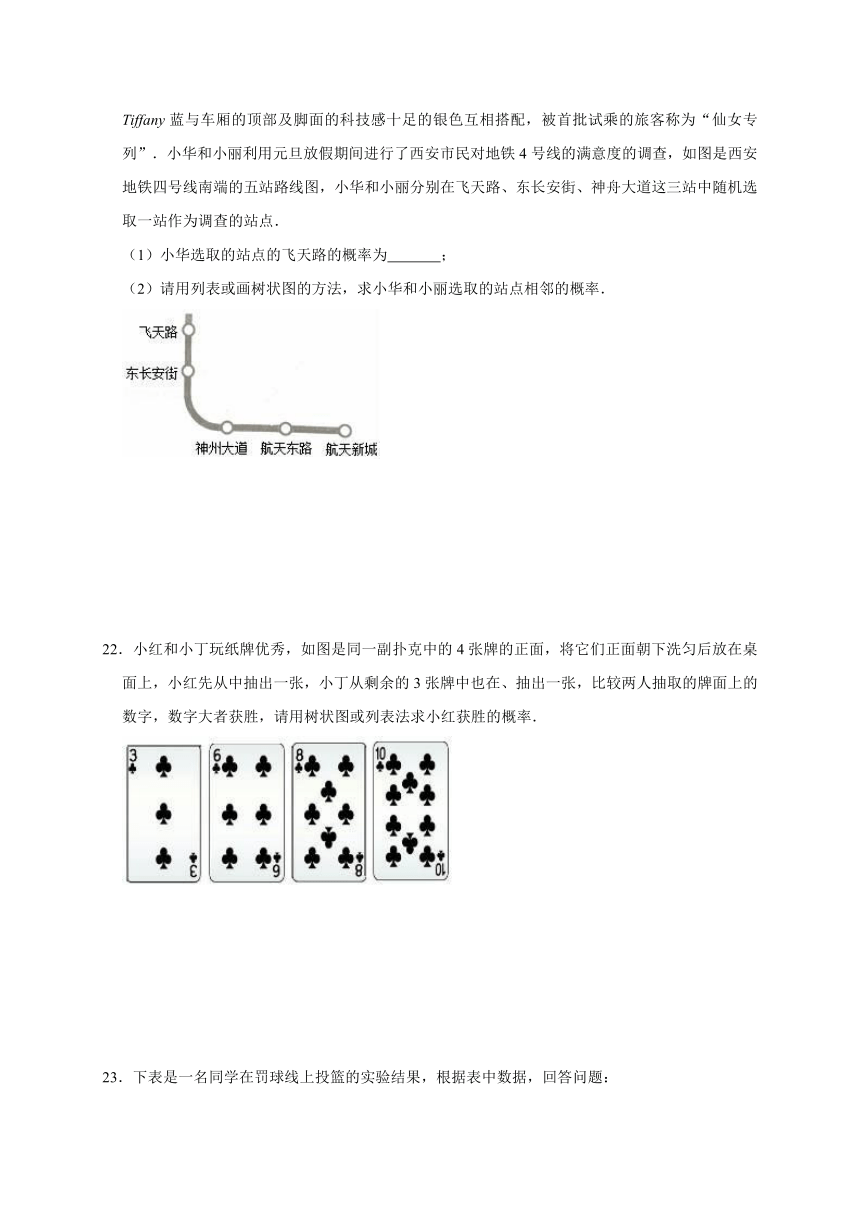
21.2018年12月16日,西安市地铁4号线带着华美的外表和深厚的文化开通试运营,列车车厢的Tiffany蓝与车厢的顶部及脚面的科技感十足的银色互相搭配,被首批试乘的旅客称为“仙女专列”.小华和小丽利用元旦放假期间进行了西安市民对地铁4号线的满意度的调查,如图是西安地铁四号线南端的五站路线图,小华和小丽分别在飞天路、东长安街、神舟大道这三站中随机选取一站作为调查的站点.
(1)小华选取的站点的飞天路的概率为 ;
(2)请用列表或画树状图的方法,求小华和小丽选取的站点相邻的概率.
22.小红和小丁玩纸牌优秀,如图是同一副扑克中的4张牌的正面,将它们正面朝下洗匀后放在桌面上,小红先从中抽出一张,小丁从剩余的3张牌中也在、抽出一张,比较两人抽取的牌面上的数字,数字大者获胜,请用树状图或列表法求小红获胜的概率.
23.下表是一名同学在罚球线上投篮的实验结果,根据表中数据,回答问题:
投篮次数(n) 50 100 150 209 250 300 500
投中次数(m) 28 60 78 104 124 153 252
投中频率() 0.56 0.60 0.52 0.52 0.49
(1)将表格补充完成;(精确到0.01)
(2)估计这名同学投篮一次,投中的概率约是多少(精确到0.1)?
(3)根据此概率,估计这名同学投篮622次,投中的次数约是多少?
24.国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分四个类别A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成条形统计图和扇形统计图(不完整).
根据以上信息,解答下列问题:
(1)D类别在扇形统计图中对应的圆心角度数是 ;
(2)将条形统计图补充完整;
(3)市扶贫办从该旗县甲乡镇3户和乙乡镇2户共5户贫困户中,随机抽取两户进行满度回访,求这两户贫困户恰好都是同一乡镇的概率.
25.现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整),请根据以上信息,解答下列问题;
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,求被选取的两名教师恰好都在20000(包含20000)以上的概率.
步数 频数 频率
0≤x<4000 8 a
4000≤x<8000 15 0.3
8000≤x<12000 12 b
12000≤x<16000 c 0.2
16000≤x<20000 3 0.06
20000≤x<24000 d 0.04
参考答案
一.选择题
1.解:A、为了解一批灯泡的使用寿命,宜采用抽样调查的方式,所以A选项错误;
B、利用树状图得到共有正正、正反、反正、反反四种可能的结果数,所以两枚硬币都是正面朝上这一事件发生的概率为,所以B选项错误;
C、掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是随机事件,所以C选项错误;
D、因为S甲2=0.4,S乙2=0.6,所以甲的方差小于乙的方差,所以甲的射击成绩较稳定,所以D选项正确.
故选:D.
2.解:画树状图为:(用A、B、C分别表示“图书馆,博物馆,科技馆”三个场馆)
共有9种等可能的结果数,其中两人恰好选择同一场馆的结果数为3,
所以两人恰好选择同一场馆的概率==.
故选:A.
3.解:在A,B,C,D四个点中任选三个点,有如下四种情况:
ABC、ABD、ACD、BCD,
其中能够组成等腰三角形的有ACD、BCD两种情况,
∴能够组成等腰三角形的概率为=,
故选:B.
4.解:画树状图为:
共有6种等可能的结果数,其中一次性取出的两个小球标号的和不小于4的结果数为5,
所以一次性取出的两个小球标号的和不小于4的概率=.
故选:D.
5.解:画树状图为:
共有9种等可能的结果数,两人中至少有一个给“好评”的结果数为5,
所以两人中至少有一个给“好评”的概率=.
故选:C.
6.解:画树状图为:
共有4种等可能的结果数,两次都是正面朝上的结果数为1,
所以两次都是正面朝上的概率=.
故选:B.
7.解:A、掷一枚质地均匀的硬币,落地时结果是“正面向上”的概率为,不符合题意;
B、掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6的概率为,符合题意;
C、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率为,不符合题意;
D、袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球的概率,不符合题意;
故选:B.
8.解:A、两试验结果虽然不完全相等,但都是正确的,故错误;
B、两种试验结果都正确,正确;
C、增加试验次数可以减小稳定值的差异,正确;
D、同一个试验的稳定值不是唯一的,正确,
故选:A.
9.解:列表如下
1 2 5
3 3 6 15
4 4 8 20
6 6 12 30
由表知,共有9种等可能结果,其中转得的两个数之积为偶数的有7种结果,
所以转得的两个数之积为偶数的概率为,
故选:C.
10.解:列表法:
1 2 3
2 2 4 6
3 3 6 9
由表知,指的两个数字作乘法运算所得的积为奇数的有2种结果,
所以指的两个数字作乘法运算所得的积为奇数的概率为=,
故选:B.
二.填空题
11.解:如果先摸出一白球,这个白球不放回,
那么第二次摸球时,有3个白球和6个红球,再摸出一球它是白球的概率是=,
故答案为:.
12.解:∵在这6种情况中,掷的点数大于4的有2种结果,
∴掷的点数大于4的概率为=,
故答案为:.
13.解:画树状图为:
共有12种等可能的结果数,其中a,b之和大于0的结果数为4,
所以a,b之和大于0的概率==.
故答案为.
14.解:画树状图为:
共有16种等可能的结果数,其中以第一次得到的放字为横坐标,第二次得到的数字为纵坐标得到的恰好在直线y=﹣x+4上的结果数为4,
所以以第一次得到的放字为横坐标,第二次得到的数字为纵坐标,得到一个点则这个点.恰好在直线y=﹣x+4上的概率==.
故答案为.
15.解:画树状图为:
共有9种等可能的结果数,其中两球上的编号的积为偶数的结果数为5,
所以两球上的编号的积为偶数的概率=.
故答案为.
16.解:画树状图为:
共有36种等可能的结果数,其中小红两次都抽到3号跑道的结果数为1,
所以小红两次都抽到3号跑道的概率=.
故答案为.
17.解:设袋中红球有x个,
根据题意,得:=0.7,
解得:x=7,
经检验:x=7是分式方程的解,
所以袋中红球有7个,
故答案为:7.
18.解:画树状图得:
∵共有16种等可能的结果,记录的两个数字的和等于0的由3种结果,
∴记录的两个数字的和等于0的概率为,
故答案为:.
三.解答题
19.解:(1)小明不一定能中奖,
故答案为:否;
(2)球的个数有1+2+3+8=14(个),而红球有1个
所以小明抽到一等奖的概率是.
(3)因为黑球的个数有8个,
所以没有中奖的概率是=,
则中奖的概率是1﹣=,
因为≠,
所以中奖和没中奖的机会不相等,
可以减少2个黑球使中奖和没中奖的机会相等(答案不唯一).
20.解:(1)点A所有可能的坐标为(2,1)、(2,2)、(2,3)、(2,4)、(2,5)、(2,6);
(2)∵在所列的6种等可能结果中,点A落在y=x+1上的有1种结果,
∴点A(x,y)在直线y=x+1上的概率为.
21.解:1)小华选取的站点的飞天路的概率为;
故答案为;
(2)画树状图为:(用A、B、C分别表示飞天路、东长安街、神舟大道这三站)
共有9种等可能的结果数,其中小华和小丽选取的站点相邻的结果数为4,
小华和小丽选取的站点相邻的概率=
22.解:画树状图为:
共有12种等可能的结果数,其中小红获胜的结果数为6,
所以小红获胜的概率==.
23.解:(1)153÷300=0.51,
252÷500≈0.50;
故答案为:0.51,0.50;
(2)估计这名同学投篮一次,投中的概率约是0.5;
(3)622×0.5=311(次).
所以估计这名同学投篮622次,投中的次数约是311次.
24.解:(1)∵被调查的总户数为50÷25%=200(户),
∴D类别在扇形统计图中对应的圆心角度数是360°×=18°,
故答案为:18°;
(2)B满意度的户数为200﹣(50+20+10)=120(户),
补全图形如下:
(3)画树状图如下:
由树状图知共有20种等可能结果,其中这两户贫困户恰好都是同一乡镇的有8种结果,
所以这两户贫困户恰好都是同一乡镇的概率为=.
25.解:(1)a=8÷50=0.16,b=12÷50=0.24,c=50×0.2=10,d=50×0.04=2,
补全频数分布直方图如下:
(2)37800×(0.2+0.06+0.04)=11340,
答:估计日行走步数超过12000步(包含12000步)的教师有11340名;
(3)设16000≤x<20000的3名教师分别为A、B、C,
20000≤x<24000的2名教师分别为X、Y,
画树状图如下:
由树状图可知,被选取的两名教师恰好都在20000步(包含20000步)以上的概率为=.
一.选择题(共10小题,每小题3分,共30分)
1.下列说法正确的是( )
A.为了解一批灯泡的使用寿命,宜采用普查方式
B.掷两枚质地均匀的硬币,两枚硬币都是正面朝上这一事件发生的概率为
C.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
D.甲乙两人在相同条件下各射击10次,他们成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
2.“学雷锋”活动月中,“飞翼”班将组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )
A. B. C. D.
3.如图,4×2的正方形网格中,在A,B,C,D四个点中任选三个点,能够组成等腰三角形的概率为( )
A.0 B. C. D.
4.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.若一次性摸出两个球,则一次性取出的两个小球标号的和不小于4的概率是( )
A. B. C. D.
5.消费者在网店购物后,将从“好评、中评、差评”中选择一种作为对卖家的评价,假设这三种评价是等可能的,若小明、小亮在某网店购买了同一商品,且都给出了评价,则两人中至少有一个给“好评”的概率为( )
A. B. C. D.
6.将一枚均匀的硬币连续抛掷两次,则两次都是正面朝上的概率等于( )
A.0.5 B.0.25 C.0.75 D.1
7.某小组在“用频率估计概率”的实验中,统计了某种频率结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )
A.掷一枚质地均匀的硬币,落地时结果是“正面向上”
B.掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C.在“石头剪刀、和”的游戏中,小明随机出的是“剪刀”
D.袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
8.在做抛硬币试验时,甲、乙两个小组画出折线统计图后发现频率的稳定值分别是50.00%和50.02%,则下列说法错误是( )
A.乙同学的试验结果是错误的
B.这两种试验结果都是正确的
C.增加试验次数可以减小稳定值的差异
D.同一个试验的稳定值不是唯一的
9.如图所示,分别用两个质地均匀的转盘转得一个数,①号转盘表示数字2的扇形对应的圆心角为120°,②号转盘表示数字3的扇形对应的圆心角也是120°,则转得的两个数之积为偶数的概率为( )
A. B. C. D.
10.如图,两个转盘中指针落在每个数字的机会均等.现在同时自由转动甲、乙两个转盘,转盘停止后,指针各自指向一个数字,用所指的两个数字作乘法运算所得的积为奇数的概率为( )
A. B. C. D.
二.填空题(共8小题,每小题3分,共24分)
11.一个口袋中装有6个红球和4个白球,这些球除颜色外完全相同,充分搅匀后随机摸出一球发现是白球,如果这个白球不放回,再摸出一球,它是白球的概率是 .
12.一枚材质均匀的骰子,六个面的点数分别是1,2,3,4,5,6,投这个骰子,掷的点数大于4的概率是 .
13.从分别写有﹣1,﹣2,1,2的四张卡片中随机抽取两张,把第一张卡片上的数字作为a,第二张卡片上的数字作为b,则a,b之和大于0的概率是 .
14.在一个不透明的箱子里有四张外形相同的卡片?卡片上分别标有数字﹣1,1,3,5.摸出一张后,记下数字,再放回,摇匀后再摸出一张,记下数字.以第一次得到的放字为横坐标,第二次得到的数字为纵坐标,得到一个点则这个点.恰好在直线y=﹣x+4上的概率是 .
15.在两个暗盒中,各自装有编号为1,2,3的三个球,球除编号外无其它区别,则在两个暗盒中各取一个球,两球上的编号的积为偶数的概率为 .
16.某校春季运动会,小红参加100米和200米的比赛,每组六人分别在1﹣﹣6号跑道同时进行比赛,问小红两次都抽到3号跑道的概率是 .
17.在一个不透明的袋子中装有3个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.7附近,则袋子中红球约有 个.
18.如图,一个转盘的盘面被等分成四个扇形区域,并分别标有数字﹣1、0、1、2若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字的和等于0的概率为 .
三.解答题(共7小题,共66分)
19.“五一”期间,某商场推出“购物满额即可抽奖”活动.商场在抽奖箱中装有1个红球、2个黄球、3个白球、8个黑球,每个球除颜色外都相同,红球、黄球、白球分别代表一、二、三等奖,黑球代表谢谢参与.获得抽奖杋会的顾客每次从箱子中摸出一个球,按相应颜色对应等级兑换奖品,每次所摸得球再放回抽奖箱,摇匀后由下一位顾客抽奖.已知小明获得1次抽奖机会.
(1)小明是否一定能中奖: ;(填是、否)
(2)求出小明抽到一等奖的概率;
(3)在这个活动中,中奖和没中奖的机会相等吗?为什么?如果不相等,可以如何改变球的个数,使中奖和没中奖的机会相等?(只写一种即可)
20.如图,把一个转盘分成六等份,依次标上数字1、2、3、4、5、6,小明和小芳分别只转动一次转盘,小明同学先转动转盘,结果指针指向2,接下来小芳转动转盘、若把小明和小芳转动转盘指针指向的数字分别记作x、y,把x、y作为点A的横、纵坐标.
(1)写出点A(x,y)所有可能的坐标;
(2)求点A(x,y)在直线y=x+1上的概率.
21.2018年12月16日,西安市地铁4号线带着华美的外表和深厚的文化开通试运营,列车车厢的Tiffany蓝与车厢的顶部及脚面的科技感十足的银色互相搭配,被首批试乘的旅客称为“仙女专列”.小华和小丽利用元旦放假期间进行了西安市民对地铁4号线的满意度的调查,如图是西安地铁四号线南端的五站路线图,小华和小丽分别在飞天路、东长安街、神舟大道这三站中随机选取一站作为调查的站点.
(1)小华选取的站点的飞天路的概率为 ;
(2)请用列表或画树状图的方法,求小华和小丽选取的站点相邻的概率.
22.小红和小丁玩纸牌优秀,如图是同一副扑克中的4张牌的正面,将它们正面朝下洗匀后放在桌面上,小红先从中抽出一张,小丁从剩余的3张牌中也在、抽出一张,比较两人抽取的牌面上的数字,数字大者获胜,请用树状图或列表法求小红获胜的概率.
23.下表是一名同学在罚球线上投篮的实验结果,根据表中数据,回答问题:
投篮次数(n) 50 100 150 209 250 300 500
投中次数(m) 28 60 78 104 124 153 252
投中频率() 0.56 0.60 0.52 0.52 0.49
(1)将表格补充完成;(精确到0.01)
(2)估计这名同学投篮一次,投中的概率约是多少(精确到0.1)?
(3)根据此概率,估计这名同学投篮622次,投中的次数约是多少?
24.国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分四个类别A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成条形统计图和扇形统计图(不完整).
根据以上信息,解答下列问题:
(1)D类别在扇形统计图中对应的圆心角度数是 ;
(2)将条形统计图补充完整;
(3)市扶贫办从该旗县甲乡镇3户和乙乡镇2户共5户贫困户中,随机抽取两户进行满度回访,求这两户贫困户恰好都是同一乡镇的概率.
25.现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整),请根据以上信息,解答下列问题;
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,求被选取的两名教师恰好都在20000(包含20000)以上的概率.
步数 频数 频率
0≤x<4000 8 a
4000≤x<8000 15 0.3
8000≤x<12000 12 b
12000≤x<16000 c 0.2
16000≤x<20000 3 0.06
20000≤x<24000 d 0.04
参考答案
一.选择题
1.解:A、为了解一批灯泡的使用寿命,宜采用抽样调查的方式,所以A选项错误;
B、利用树状图得到共有正正、正反、反正、反反四种可能的结果数,所以两枚硬币都是正面朝上这一事件发生的概率为,所以B选项错误;
C、掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是随机事件,所以C选项错误;
D、因为S甲2=0.4,S乙2=0.6,所以甲的方差小于乙的方差,所以甲的射击成绩较稳定,所以D选项正确.
故选:D.
2.解:画树状图为:(用A、B、C分别表示“图书馆,博物馆,科技馆”三个场馆)
共有9种等可能的结果数,其中两人恰好选择同一场馆的结果数为3,
所以两人恰好选择同一场馆的概率==.
故选:A.
3.解:在A,B,C,D四个点中任选三个点,有如下四种情况:
ABC、ABD、ACD、BCD,
其中能够组成等腰三角形的有ACD、BCD两种情况,
∴能够组成等腰三角形的概率为=,
故选:B.
4.解:画树状图为:
共有6种等可能的结果数,其中一次性取出的两个小球标号的和不小于4的结果数为5,
所以一次性取出的两个小球标号的和不小于4的概率=.
故选:D.
5.解:画树状图为:
共有9种等可能的结果数,两人中至少有一个给“好评”的结果数为5,
所以两人中至少有一个给“好评”的概率=.
故选:C.
6.解:画树状图为:
共有4种等可能的结果数,两次都是正面朝上的结果数为1,
所以两次都是正面朝上的概率=.
故选:B.
7.解:A、掷一枚质地均匀的硬币,落地时结果是“正面向上”的概率为,不符合题意;
B、掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6的概率为,符合题意;
C、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率为,不符合题意;
D、袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球的概率,不符合题意;
故选:B.
8.解:A、两试验结果虽然不完全相等,但都是正确的,故错误;
B、两种试验结果都正确,正确;
C、增加试验次数可以减小稳定值的差异,正确;
D、同一个试验的稳定值不是唯一的,正确,
故选:A.
9.解:列表如下
1 2 5
3 3 6 15
4 4 8 20
6 6 12 30
由表知,共有9种等可能结果,其中转得的两个数之积为偶数的有7种结果,
所以转得的两个数之积为偶数的概率为,
故选:C.
10.解:列表法:
1 2 3
2 2 4 6
3 3 6 9
由表知,指的两个数字作乘法运算所得的积为奇数的有2种结果,
所以指的两个数字作乘法运算所得的积为奇数的概率为=,
故选:B.
二.填空题
11.解:如果先摸出一白球,这个白球不放回,
那么第二次摸球时,有3个白球和6个红球,再摸出一球它是白球的概率是=,
故答案为:.
12.解:∵在这6种情况中,掷的点数大于4的有2种结果,
∴掷的点数大于4的概率为=,
故答案为:.
13.解:画树状图为:
共有12种等可能的结果数,其中a,b之和大于0的结果数为4,
所以a,b之和大于0的概率==.
故答案为.
14.解:画树状图为:
共有16种等可能的结果数,其中以第一次得到的放字为横坐标,第二次得到的数字为纵坐标得到的恰好在直线y=﹣x+4上的结果数为4,
所以以第一次得到的放字为横坐标,第二次得到的数字为纵坐标,得到一个点则这个点.恰好在直线y=﹣x+4上的概率==.
故答案为.
15.解:画树状图为:
共有9种等可能的结果数,其中两球上的编号的积为偶数的结果数为5,
所以两球上的编号的积为偶数的概率=.
故答案为.
16.解:画树状图为:
共有36种等可能的结果数,其中小红两次都抽到3号跑道的结果数为1,
所以小红两次都抽到3号跑道的概率=.
故答案为.
17.解:设袋中红球有x个,
根据题意,得:=0.7,
解得:x=7,
经检验:x=7是分式方程的解,
所以袋中红球有7个,
故答案为:7.
18.解:画树状图得:
∵共有16种等可能的结果,记录的两个数字的和等于0的由3种结果,
∴记录的两个数字的和等于0的概率为,
故答案为:.
三.解答题
19.解:(1)小明不一定能中奖,
故答案为:否;
(2)球的个数有1+2+3+8=14(个),而红球有1个
所以小明抽到一等奖的概率是.
(3)因为黑球的个数有8个,
所以没有中奖的概率是=,
则中奖的概率是1﹣=,
因为≠,
所以中奖和没中奖的机会不相等,
可以减少2个黑球使中奖和没中奖的机会相等(答案不唯一).
20.解:(1)点A所有可能的坐标为(2,1)、(2,2)、(2,3)、(2,4)、(2,5)、(2,6);
(2)∵在所列的6种等可能结果中,点A落在y=x+1上的有1种结果,
∴点A(x,y)在直线y=x+1上的概率为.
21.解:1)小华选取的站点的飞天路的概率为;
故答案为;
(2)画树状图为:(用A、B、C分别表示飞天路、东长安街、神舟大道这三站)
共有9种等可能的结果数,其中小华和小丽选取的站点相邻的结果数为4,
小华和小丽选取的站点相邻的概率=
22.解:画树状图为:
共有12种等可能的结果数,其中小红获胜的结果数为6,
所以小红获胜的概率==.
23.解:(1)153÷300=0.51,
252÷500≈0.50;
故答案为:0.51,0.50;
(2)估计这名同学投篮一次,投中的概率约是0.5;
(3)622×0.5=311(次).
所以估计这名同学投篮622次,投中的次数约是311次.
24.解:(1)∵被调查的总户数为50÷25%=200(户),
∴D类别在扇形统计图中对应的圆心角度数是360°×=18°,
故答案为:18°;
(2)B满意度的户数为200﹣(50+20+10)=120(户),
补全图形如下:
(3)画树状图如下:
由树状图知共有20种等可能结果,其中这两户贫困户恰好都是同一乡镇的有8种结果,
所以这两户贫困户恰好都是同一乡镇的概率为=.
25.解:(1)a=8÷50=0.16,b=12÷50=0.24,c=50×0.2=10,d=50×0.04=2,
补全频数分布直方图如下:
(2)37800×(0.2+0.06+0.04)=11340,
答:估计日行走步数超过12000步(包含12000步)的教师有11340名;
(3)设16000≤x<20000的3名教师分别为A、B、C,
20000≤x<24000的2名教师分别为X、Y,
画树状图如下:
由树状图可知,被选取的两名教师恰好都在20000步(包含20000步)以上的概率为=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
