人教版七年级数学上册第四章几何图形初步4.3 角同步测试(含解析)
文档属性
| 名称 | 人教版七年级数学上册第四章几何图形初步4.3 角同步测试(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-21 00:00:00 | ||
图片预览


文档简介
人教版七年级数学上册 第四章 几何图形初步 第三节 角 同步测试
一.选择题(共10小题,每小题3分,共30分)
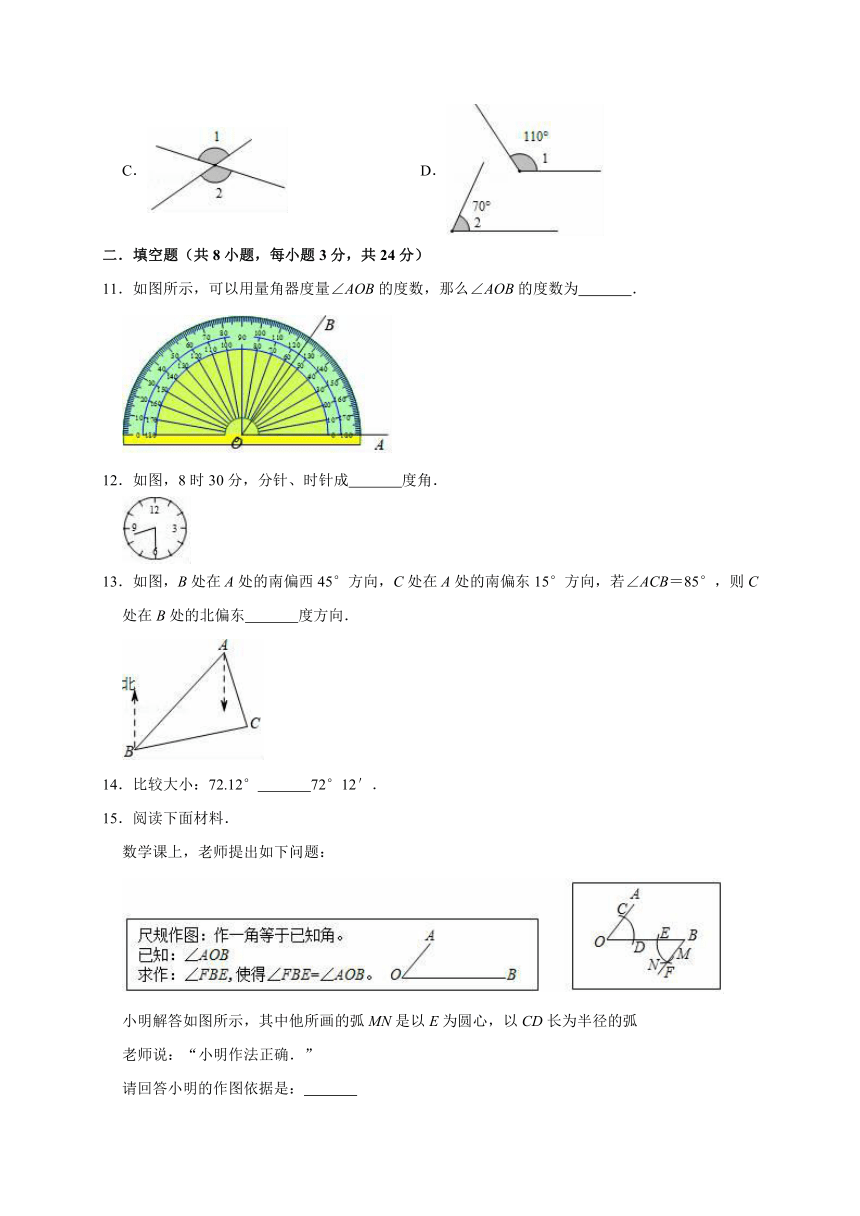
1.如图,直线m外有一点O,点A是m上一点,当点A在m上运动时,下列选项一定成立的是( )
A.∠α>∠β B.∠α<∠β C.∠α=∠β D.∠α+∠β=180°
2.如图,钟表上10点整时,时针与分针所成的角是( )
A.30° B.60° C.90° D.120°
3.如图表示点A的位置,正确的是( )
A.距离O点3km的地方
B.在O点北偏东40°方向,距O点3km的地方
C.在O点东偏北40°的方向上
D.在O点北偏东50°方向,距O点3m的地方
4.下列换算中,错误的是( )
A.0.25°=900″ B.16°5′24″=16.09°
C.47.28°=47°16′48″ D.80.5°=80°50′
5.用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,错误的作法有( )
A.1种 B.2种 C.3种 D.4种
6.下列说法:①若C是AB的中点,则AC=BC;②若AC=BC,则点C是AB的中点;③若OC是∠AOB的平分线,则∠AOC=∠AOB;④若∠AOC=∠AOB,则OC是∠AOB的平分线,其中正确的有( )
A.1个 B.3个 C.2个 D.4个
7.如图,矩形纸片ABCD,M为AD边的中点将纸片沿BM、CM折叠,使A点落在A1处,D点落在D1处,若∠1=30°,则∠BMC=( )
A.75° B.150° C.120° D.105°
8.如图,图1和图2中,两个剪刀张开的角度α和β的大小关系为( )
A.α>β B.α<β C.α=β D.不能确定
9.若锐角α的补角度数为m,则锐角α的余角度数为( )
A.m﹣90° B.45°+m C.180°﹣m D.90﹣m
10.下列图形中,∠1与∠2不是互补关系的是( )
A. B.
C. D.
二.填空题(共8小题,每小题3分,共24分)
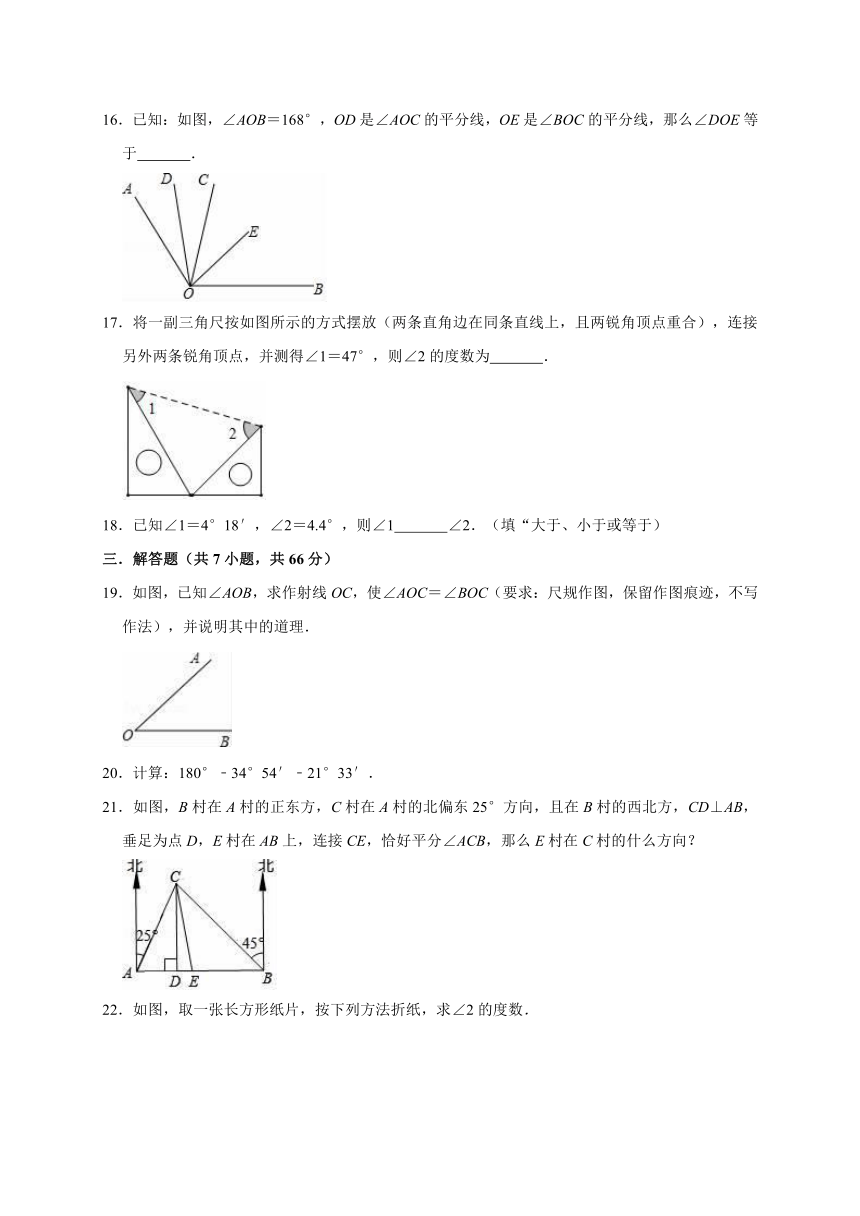
11.如图所示,可以用量角器度量∠AOB的度数,那么∠AOB的度数为 .
12.如图,8时30分,分针、时针成 度角.
13.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,若∠ACB=85°,则C处在B处的北偏东 度方向.
14.比较大小:72.12° 72°12′.
15.阅读下面材料.
数学课上,老师提出如下问题:
小明解答如图所示,其中他所画的弧MN是以E为圆心,以CD长为半径的弧
老师说:“小明作法正确.”
请回答小明的作图依据是:
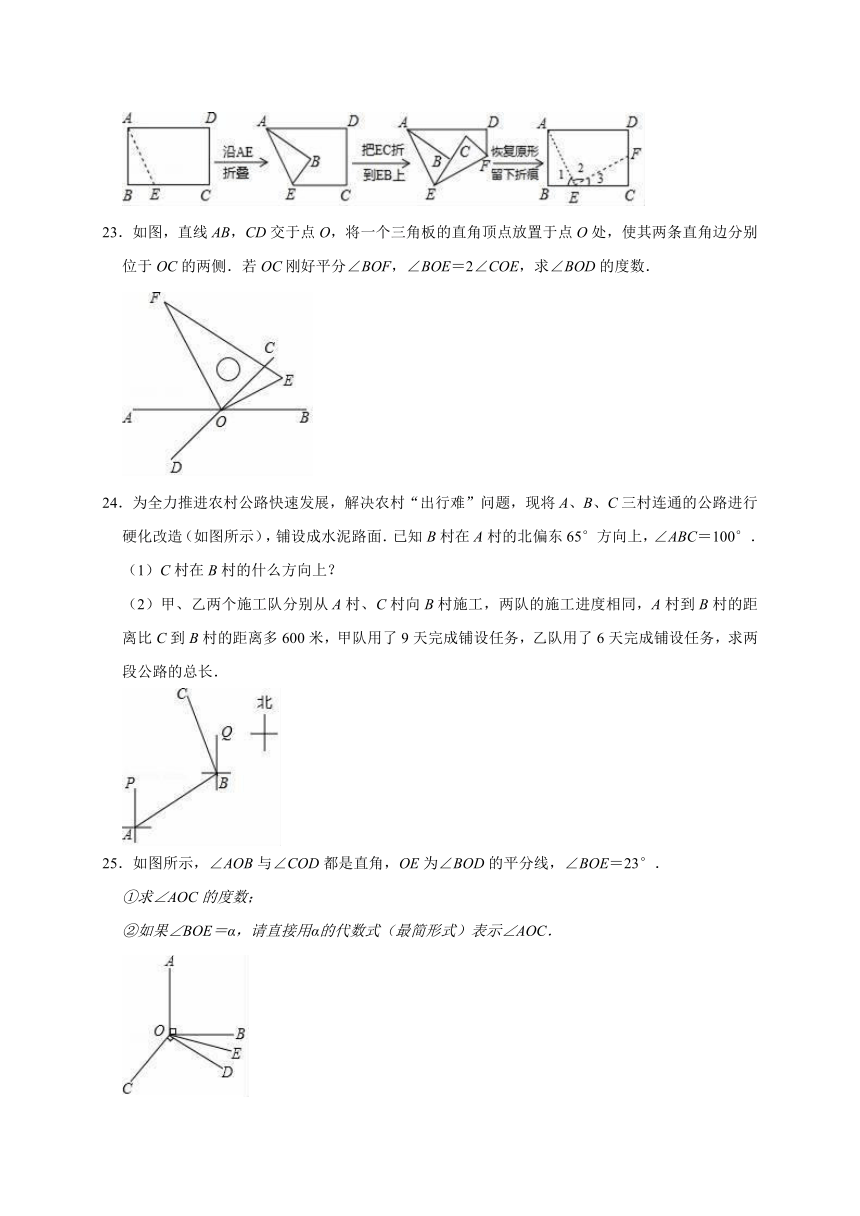
16.已知:如图,∠AOB=168°,OD是∠AOC的平分线,OE是∠BOC的平分线,那么∠DOE等于 .
17.将一副三角尺按如图所示的方式摆放(两条直角边在同条直线上,且两锐角顶点重合),连接另外两条锐角顶点,并测得∠1=47°,则∠2的度数为 .
18.已知∠1=4°18′,∠2=4.4°,则∠1 ∠2.(填“大于、小于或等于)
三.解答题(共7小题,共66分)
19.如图,已知∠AOB,求作射线OC,使∠AOC=∠BOC(要求:尺规作图,保留作图痕迹,不写作法),并说明其中的道理.
20.计算:180°﹣34°54′﹣21°33′.
21.如图,B村在A村的正东方,C村在A村的北偏东25°方向,且在B村的西北方,CD⊥AB,垂足为点D,E村在AB上,连接CE,恰好平分∠ACB,那么E村在C村的什么方向?
22.如图,取一张长方形纸片,按下列方法折纸,求∠2的度数.
23.如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠BOD的度数.
24.为全力推进农村公路快速发展,解决农村“出行难”问题,现将A、B、C三村连通的公路进行硬化改造(如图所示),铺设成水泥路面.已知B村在A村的北偏东65°方向上,∠ABC=100°.
(1)C村在B村的什么方向上?
(2)甲、乙两个施工队分别从A村、C村向B村施工,两队的施工进度相同,A村到B村的距离比C到B村的距离多600米,甲队用了9天完成铺设任务,乙队用了6天完成铺设任务,求两段公路的总长.
25.如图所示,∠AOB与∠COD都是直角,OE为∠BOD的平分线,∠BOE=23°.
①求∠AOC的度数;
②如果∠BOE=α,请直接用α的代数式(最简形式)表示∠AOC.
参考答案
一.选择题
1.【解答】解:由图可得,∠α与∠β是邻补角,
∴∠α+∠β=180°,故D选项正确,
而∠α>∠β、∠α=∠β、∠α<∠β都不一定成立,
故选:D.
2.【解答】解:∵钟面分成12个大格,每格的度数为30°,
∴钟表上10点整时,时针与分针所成的角是60°.
故选:B.
3.【解答】解:由图可得,点A在O点北偏东50°方向,距O点3m的地方,
故选:D.
4.【解答】解:A、0.25°=15′=900″,正确,不合题意;
B、16°5′24″=16°5.4′=16.09°,正确,不合题意;
C、47.28°=47°16′48″,正确,不合题意;
D、80.5°=80°30′,错误,符合题意.
故选:D.
5.【解答】解:①根据垂径定理作图的方法可知,CD是Rt△ABC斜边AB上的高线,此作图正确;
②根据直径所对的圆周角是直角的方法可知,CD是Rt△ABC斜边AB上的高线,此作图正确;
③根据相交两圆的公共弦的性质可知,CD是Rt△ABC斜边AB上的高线,此作图正确;
④无法证明CD是Rt△ABC斜边AB上的高线,此作图错误.
故选:A.
6.【解答】解:①若C是AB的中点,则AC=BC,该说法正确;
②若AC=BC,则点C不一定是AB的中点,该说法错误;
③若OC是∠AOB的平分线,则∠AOC=∠AOB,该说法正确;
④若∠AOC=∠AOB,则OC不一定是∠AOB的平分线,该说法错误;
故选:C.
7.【解答】解:?∠1=30°,
∴∠AMA1+∠DMD1=180﹣30=150°.
∴∠BMA1+∠CMD1=75°.
∴∠BMC=∠BMA1+∠CMD1+∠1=105°.
故选:D.
8.【解答】解:由图可得,两个剪刀张开的角度α和β的大小关系为α=β,
故选:C.
9.【解答】解:∵锐角α的补角度数为m,
∴锐角α的度数为:180°﹣m,
∴锐角α的余角是90°﹣(180°﹣m)=m﹣90°.
故选:A.
10.【解答】解:A.∠1与∠2是互补关系,故本选项不合题意;
B.由平行线的性质可知∠1与∠2是互补关系,故本选项不合题意;
C.由对顶角的定义可知∠1与∠2是对顶角,不一定具有互补关系,故本选项符合题意;
D.∠1+∠2=180°,即∠1与∠2是互补关系,故本选项不合题意.
故选:C.
二.填空题
11.【分析】由图形可直接得出.
【解答】解:由图形所示,∠AOB的度数为55°,
故答案为:55°
【点评】本题主要考查了角的度量,量角器的使用方法,正确使用量角器是解题的关键.
12.【分析】利用钟表表盘的特征进行分析:钟表上有12个数字,每相邻两个数字之间的夹角为30°,即一个大格是30°,计算出上午8:30,时针和分针中间相差大格子的数量,然后用“30°×相差的大格子的数量”解答即可.
【解答】解:8:30,时针和分针中间相差2.5个大格.每个大格为30°,
所以8:30分针与时针的夹角是:2.5×30°=75°;
故答案为:75.
【点评】考查了钟面角.钟表上12个数字,每相邻两个数字之间的夹角为30°.
13.【分析】方向角是从正北或正南方向到目标方向所形成的小于90°的角.
【解答】解:∵B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,
∴∠BAC=45°+15°=60°,
∵∠ACB=85°,
∴∠ABC=180°﹣60°﹣85°=35°,
∴C处在B处的北偏东45°+35°=80°,
故答案为80.
【点评】本题考查了方向角,熟练利用平行线的性质与三角形的内角和定理是解题的关键.
14.【分析】将72°12′化成72.2°,然后再进行比较即可.
【解答】解:72°12′=72°+12°÷60=72.2°,
∴72.12°<72°12′,
故答案为:<.
【点评】此题主要考查了角的大小比较,以及度分秒的换算,1度=60分,即1°=60′,1分=60秒,即1′=60″.
15.【分析】利用“SSS“可证明△BEF≌△OCD,从而可得到∠EBF=∠COD.
【解答】解:由作法得OC=OD=BE=BF,EF=CD,
所以△BEF≌△OCD(SSS).
所以∠EBF=∠COD,
故答案为SSS.
【点评】本题考查了作图﹣基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).
16.【分析】根据角平分线定义得出∠DOC=∠AOC,∠EOC=∠BOC,求出∠DOE=∠AOB,代入求出即可.
【解答】解:∵OD是∠AOC的角平分线,OE是∠BOC的角平分线,
∴∠DOC=∠AOC,∠EOC=∠BOC,
∴∠DOE=∠DOC+∠EOC
=∠AOC+∠BOC
=(∠AOC+∠BOC)
=∠AOB
=×168°
=84°
故答案为:84°
【点评】此题考查了角平分线的定义,将两条角平分线组成的夹角转换为∠AOB的一半为解题关键.
17.【分析】由三角尺角的特殊性,利用平角定义及三角形内角和定理即可求出.
【解答】解:如图所示,
∠3=180°﹣60°﹣45°=75°,
则∠2=180°﹣∠1﹣∠3=180°﹣47°﹣75°=58°.
故答案为:58°
【点评】本题考查平角定义及三角形内角和定理,并且要明确知道三角尺各角的度数,进行计算.
18.【分析】依据度分秒的换算,即可得到∠2=4.4°=4°24′,进而得出∠1与∠2的大小关系.
【解答】解:∵∠1=4°18′,∠2=4.4°=4°24′,
∴∠1<∠2,
故答案为:小于.
【点评】本题主要考查了角的大小比较,注意角的度数越大,角越大.
三.解答题
19.【解答】解:如图,射线OC或OC′为所作.
通过证明△ODP≌△OEP得到∠DOP=∠EOP,
然后根据等角的补角相等得到∠AOC′=∠BOC′.
20.【解答】解:原式=145°+35°﹣34°54′﹣21°33′
=145°+6′﹣21°33′
=123°+22°+6′﹣21°33′
=123°33′.
21.【解答】解:根据题意,可得:∠CAB=65°,∠ABC=45°,
∵在△CAB中,∠CAB+∠ABC+∠ACB=180°,
∴65°+45°+∠ACB=180°,
∴∠ACB=70°,
∵CE平分∠ACB,
∴∠ACE=∠ACB=35°,
∵CD⊥AB,
∴∠ADC=90°,
∵在△CAD中,∠CAB+∠ADC+∠ACD=180°,
∴∠ACD=25°,
∴∠DCE=∠ACE﹣∠ACD=35°﹣25°=10°,
∴E村在C村的南偏东10°.
22.【解答】解:根据折叠的性质可知,∠1=∠AEB,∠3=∠FEC,
∵∠1+∠AEB+∠3+∠FEC=180°,
∴2(∠1+∠3)=180°,即∠1+∠3=90°,
∴∠2=90°.
23.【解答】解:设∠COE=α,则∠BOE=2α,∠BOC=3α,
∵∠AOE=90°,
∴∠BOF=90°+2α,
又∵OC平分∠BOF,
∴∠BOC=∠BOF=45°+α,
∴3α=45°+α,
解得α=22.5°,
∴∠BOC=67.5°,
∴∠BOD=180°﹣∠BOC=112.5°.
24.【解答】解:(1)由题意,得∠PAB=65°,
∵表示同一方向的射线是平行的,即AP∥BQ,
∴∠PAB+∠QBA=180°,
∴∠QBA=180°﹣∠PAB=180°﹣65°=115°,
∵∠ABC=100°,
∴∠CBQ=∠QBA﹣∠ABC=115°﹣100°=15°,
∴C村在B村的北偏西15°方向上;
(2)设每个施工队每天铺设x米,由题意,得
9x﹣6x=600,
解得x=200,
∴9x+6x=9×200+6×200=3000,
答:两段公路的总长3000米.
25.【解答】解:
①∵OE为∠BOD的平分线,∠BOE=23°
∴∠BOD=2∠BOE=2×23°=46°
∴∠AOC=360°﹣∠AOB﹣∠COD﹣∠BOD=360°﹣90°﹣90°﹣46°=134°
故∠AOC=134°
②∵∠BOE=α,OE为∠BOD的平分线
∴∠AOC=360°﹣∠AOB﹣∠COD﹣∠BOD=360°﹣90°﹣90°﹣2α=180°﹣2α
故用α的代数式(最简形式)表示∠AOC为:180°﹣2α
一.选择题(共10小题,每小题3分,共30分)
1.如图,直线m外有一点O,点A是m上一点,当点A在m上运动时,下列选项一定成立的是( )
A.∠α>∠β B.∠α<∠β C.∠α=∠β D.∠α+∠β=180°
2.如图,钟表上10点整时,时针与分针所成的角是( )
A.30° B.60° C.90° D.120°
3.如图表示点A的位置,正确的是( )
A.距离O点3km的地方
B.在O点北偏东40°方向,距O点3km的地方
C.在O点东偏北40°的方向上
D.在O点北偏东50°方向,距O点3m的地方
4.下列换算中,错误的是( )
A.0.25°=900″ B.16°5′24″=16.09°
C.47.28°=47°16′48″ D.80.5°=80°50′
5.用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,错误的作法有( )
A.1种 B.2种 C.3种 D.4种
6.下列说法:①若C是AB的中点,则AC=BC;②若AC=BC,则点C是AB的中点;③若OC是∠AOB的平分线,则∠AOC=∠AOB;④若∠AOC=∠AOB,则OC是∠AOB的平分线,其中正确的有( )
A.1个 B.3个 C.2个 D.4个
7.如图,矩形纸片ABCD,M为AD边的中点将纸片沿BM、CM折叠,使A点落在A1处,D点落在D1处,若∠1=30°,则∠BMC=( )
A.75° B.150° C.120° D.105°
8.如图,图1和图2中,两个剪刀张开的角度α和β的大小关系为( )
A.α>β B.α<β C.α=β D.不能确定
9.若锐角α的补角度数为m,则锐角α的余角度数为( )
A.m﹣90° B.45°+m C.180°﹣m D.90﹣m
10.下列图形中,∠1与∠2不是互补关系的是( )
A. B.
C. D.
二.填空题(共8小题,每小题3分,共24分)
11.如图所示,可以用量角器度量∠AOB的度数,那么∠AOB的度数为 .
12.如图,8时30分,分针、时针成 度角.
13.如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,若∠ACB=85°,则C处在B处的北偏东 度方向.
14.比较大小:72.12° 72°12′.
15.阅读下面材料.
数学课上,老师提出如下问题:
小明解答如图所示,其中他所画的弧MN是以E为圆心,以CD长为半径的弧
老师说:“小明作法正确.”
请回答小明的作图依据是:
16.已知:如图,∠AOB=168°,OD是∠AOC的平分线,OE是∠BOC的平分线,那么∠DOE等于 .
17.将一副三角尺按如图所示的方式摆放(两条直角边在同条直线上,且两锐角顶点重合),连接另外两条锐角顶点,并测得∠1=47°,则∠2的度数为 .
18.已知∠1=4°18′,∠2=4.4°,则∠1 ∠2.(填“大于、小于或等于)
三.解答题(共7小题,共66分)
19.如图,已知∠AOB,求作射线OC,使∠AOC=∠BOC(要求:尺规作图,保留作图痕迹,不写作法),并说明其中的道理.
20.计算:180°﹣34°54′﹣21°33′.
21.如图,B村在A村的正东方,C村在A村的北偏东25°方向,且在B村的西北方,CD⊥AB,垂足为点D,E村在AB上,连接CE,恰好平分∠ACB,那么E村在C村的什么方向?
22.如图,取一张长方形纸片,按下列方法折纸,求∠2的度数.
23.如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠BOD的度数.
24.为全力推进农村公路快速发展,解决农村“出行难”问题,现将A、B、C三村连通的公路进行硬化改造(如图所示),铺设成水泥路面.已知B村在A村的北偏东65°方向上,∠ABC=100°.
(1)C村在B村的什么方向上?
(2)甲、乙两个施工队分别从A村、C村向B村施工,两队的施工进度相同,A村到B村的距离比C到B村的距离多600米,甲队用了9天完成铺设任务,乙队用了6天完成铺设任务,求两段公路的总长.
25.如图所示,∠AOB与∠COD都是直角,OE为∠BOD的平分线,∠BOE=23°.
①求∠AOC的度数;
②如果∠BOE=α,请直接用α的代数式(最简形式)表示∠AOC.
参考答案
一.选择题
1.【解答】解:由图可得,∠α与∠β是邻补角,
∴∠α+∠β=180°,故D选项正确,
而∠α>∠β、∠α=∠β、∠α<∠β都不一定成立,
故选:D.
2.【解答】解:∵钟面分成12个大格,每格的度数为30°,
∴钟表上10点整时,时针与分针所成的角是60°.
故选:B.
3.【解答】解:由图可得,点A在O点北偏东50°方向,距O点3m的地方,
故选:D.
4.【解答】解:A、0.25°=15′=900″,正确,不合题意;
B、16°5′24″=16°5.4′=16.09°,正确,不合题意;
C、47.28°=47°16′48″,正确,不合题意;
D、80.5°=80°30′,错误,符合题意.
故选:D.
5.【解答】解:①根据垂径定理作图的方法可知,CD是Rt△ABC斜边AB上的高线,此作图正确;
②根据直径所对的圆周角是直角的方法可知,CD是Rt△ABC斜边AB上的高线,此作图正确;
③根据相交两圆的公共弦的性质可知,CD是Rt△ABC斜边AB上的高线,此作图正确;
④无法证明CD是Rt△ABC斜边AB上的高线,此作图错误.
故选:A.
6.【解答】解:①若C是AB的中点,则AC=BC,该说法正确;
②若AC=BC,则点C不一定是AB的中点,该说法错误;
③若OC是∠AOB的平分线,则∠AOC=∠AOB,该说法正确;
④若∠AOC=∠AOB,则OC不一定是∠AOB的平分线,该说法错误;
故选:C.
7.【解答】解:?∠1=30°,
∴∠AMA1+∠DMD1=180﹣30=150°.
∴∠BMA1+∠CMD1=75°.
∴∠BMC=∠BMA1+∠CMD1+∠1=105°.
故选:D.
8.【解答】解:由图可得,两个剪刀张开的角度α和β的大小关系为α=β,
故选:C.
9.【解答】解:∵锐角α的补角度数为m,
∴锐角α的度数为:180°﹣m,
∴锐角α的余角是90°﹣(180°﹣m)=m﹣90°.
故选:A.
10.【解答】解:A.∠1与∠2是互补关系,故本选项不合题意;
B.由平行线的性质可知∠1与∠2是互补关系,故本选项不合题意;
C.由对顶角的定义可知∠1与∠2是对顶角,不一定具有互补关系,故本选项符合题意;
D.∠1+∠2=180°,即∠1与∠2是互补关系,故本选项不合题意.
故选:C.
二.填空题
11.【分析】由图形可直接得出.
【解答】解:由图形所示,∠AOB的度数为55°,
故答案为:55°
【点评】本题主要考查了角的度量,量角器的使用方法,正确使用量角器是解题的关键.
12.【分析】利用钟表表盘的特征进行分析:钟表上有12个数字,每相邻两个数字之间的夹角为30°,即一个大格是30°,计算出上午8:30,时针和分针中间相差大格子的数量,然后用“30°×相差的大格子的数量”解答即可.
【解答】解:8:30,时针和分针中间相差2.5个大格.每个大格为30°,
所以8:30分针与时针的夹角是:2.5×30°=75°;
故答案为:75.
【点评】考查了钟面角.钟表上12个数字,每相邻两个数字之间的夹角为30°.
13.【分析】方向角是从正北或正南方向到目标方向所形成的小于90°的角.
【解答】解:∵B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,
∴∠BAC=45°+15°=60°,
∵∠ACB=85°,
∴∠ABC=180°﹣60°﹣85°=35°,
∴C处在B处的北偏东45°+35°=80°,
故答案为80.
【点评】本题考查了方向角,熟练利用平行线的性质与三角形的内角和定理是解题的关键.
14.【分析】将72°12′化成72.2°,然后再进行比较即可.
【解答】解:72°12′=72°+12°÷60=72.2°,
∴72.12°<72°12′,
故答案为:<.
【点评】此题主要考查了角的大小比较,以及度分秒的换算,1度=60分,即1°=60′,1分=60秒,即1′=60″.
15.【分析】利用“SSS“可证明△BEF≌△OCD,从而可得到∠EBF=∠COD.
【解答】解:由作法得OC=OD=BE=BF,EF=CD,
所以△BEF≌△OCD(SSS).
所以∠EBF=∠COD,
故答案为SSS.
【点评】本题考查了作图﹣基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).
16.【分析】根据角平分线定义得出∠DOC=∠AOC,∠EOC=∠BOC,求出∠DOE=∠AOB,代入求出即可.
【解答】解:∵OD是∠AOC的角平分线,OE是∠BOC的角平分线,
∴∠DOC=∠AOC,∠EOC=∠BOC,
∴∠DOE=∠DOC+∠EOC
=∠AOC+∠BOC
=(∠AOC+∠BOC)
=∠AOB
=×168°
=84°
故答案为:84°
【点评】此题考查了角平分线的定义,将两条角平分线组成的夹角转换为∠AOB的一半为解题关键.
17.【分析】由三角尺角的特殊性,利用平角定义及三角形内角和定理即可求出.
【解答】解:如图所示,
∠3=180°﹣60°﹣45°=75°,
则∠2=180°﹣∠1﹣∠3=180°﹣47°﹣75°=58°.
故答案为:58°
【点评】本题考查平角定义及三角形内角和定理,并且要明确知道三角尺各角的度数,进行计算.
18.【分析】依据度分秒的换算,即可得到∠2=4.4°=4°24′,进而得出∠1与∠2的大小关系.
【解答】解:∵∠1=4°18′,∠2=4.4°=4°24′,
∴∠1<∠2,
故答案为:小于.
【点评】本题主要考查了角的大小比较,注意角的度数越大,角越大.
三.解答题
19.【解答】解:如图,射线OC或OC′为所作.
通过证明△ODP≌△OEP得到∠DOP=∠EOP,
然后根据等角的补角相等得到∠AOC′=∠BOC′.
20.【解答】解:原式=145°+35°﹣34°54′﹣21°33′
=145°+6′﹣21°33′
=123°+22°+6′﹣21°33′
=123°33′.
21.【解答】解:根据题意,可得:∠CAB=65°,∠ABC=45°,
∵在△CAB中,∠CAB+∠ABC+∠ACB=180°,
∴65°+45°+∠ACB=180°,
∴∠ACB=70°,
∵CE平分∠ACB,
∴∠ACE=∠ACB=35°,
∵CD⊥AB,
∴∠ADC=90°,
∵在△CAD中,∠CAB+∠ADC+∠ACD=180°,
∴∠ACD=25°,
∴∠DCE=∠ACE﹣∠ACD=35°﹣25°=10°,
∴E村在C村的南偏东10°.
22.【解答】解:根据折叠的性质可知,∠1=∠AEB,∠3=∠FEC,
∵∠1+∠AEB+∠3+∠FEC=180°,
∴2(∠1+∠3)=180°,即∠1+∠3=90°,
∴∠2=90°.
23.【解答】解:设∠COE=α,则∠BOE=2α,∠BOC=3α,
∵∠AOE=90°,
∴∠BOF=90°+2α,
又∵OC平分∠BOF,
∴∠BOC=∠BOF=45°+α,
∴3α=45°+α,
解得α=22.5°,
∴∠BOC=67.5°,
∴∠BOD=180°﹣∠BOC=112.5°.
24.【解答】解:(1)由题意,得∠PAB=65°,
∵表示同一方向的射线是平行的,即AP∥BQ,
∴∠PAB+∠QBA=180°,
∴∠QBA=180°﹣∠PAB=180°﹣65°=115°,
∵∠ABC=100°,
∴∠CBQ=∠QBA﹣∠ABC=115°﹣100°=15°,
∴C村在B村的北偏西15°方向上;
(2)设每个施工队每天铺设x米,由题意,得
9x﹣6x=600,
解得x=200,
∴9x+6x=9×200+6×200=3000,
答:两段公路的总长3000米.
25.【解答】解:
①∵OE为∠BOD的平分线,∠BOE=23°
∴∠BOD=2∠BOE=2×23°=46°
∴∠AOC=360°﹣∠AOB﹣∠COD﹣∠BOD=360°﹣90°﹣90°﹣46°=134°
故∠AOC=134°
②∵∠BOE=α,OE为∠BOD的平分线
∴∠AOC=360°﹣∠AOB﹣∠COD﹣∠BOD=360°﹣90°﹣90°﹣2α=180°﹣2α
故用α的代数式(最简形式)表示∠AOC为:180°﹣2α
