人教版七年级数学上册第四章几何图形初步4.1几何图形同步测试(含解析)
文档属性
| 名称 | 人教版七年级数学上册第四章几何图形初步4.1几何图形同步测试(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 193.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-21 21:50:12 | ||
图片预览

文档简介
人教版七年级数学上册 第四章 几何图形初步 第一节 几何图形 同步测试
一.选择题(共10小题,每小题3分,共30分)
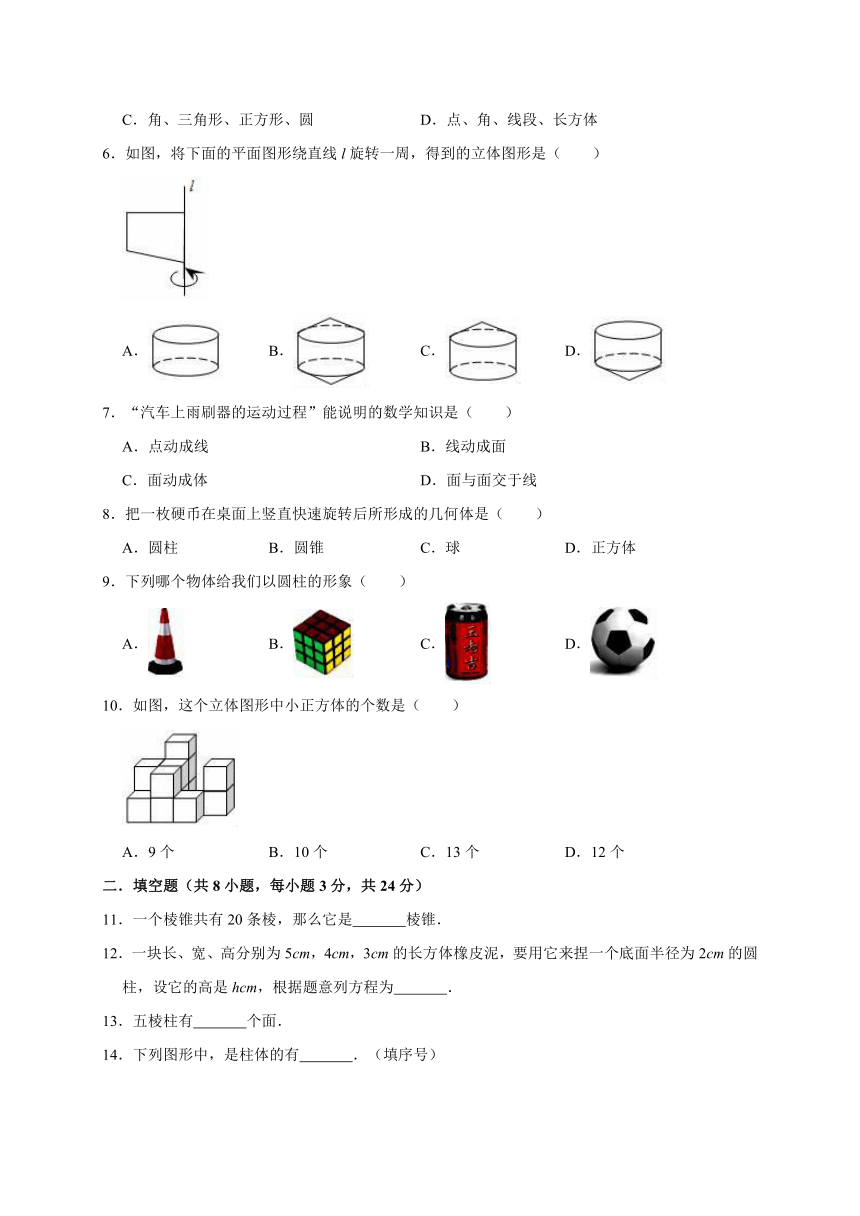
1.下列四个几何体中,是三棱柱的为( )
A. B.
C. D.
2.如图图中,含有曲面的几何体编号( )
A.①② B.①③ C.②③ D.②④
3.图中的几何体有( )条棱.
A.3 B.4 C.5 D.6
4.如图是交通禁止驶入标志,组成这个标志的几何图形有( )
A.圆、长方形 B.圆、线段 C.球、长方形 D.球、线段
5.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥 B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆 D.点、角、线段、长方体
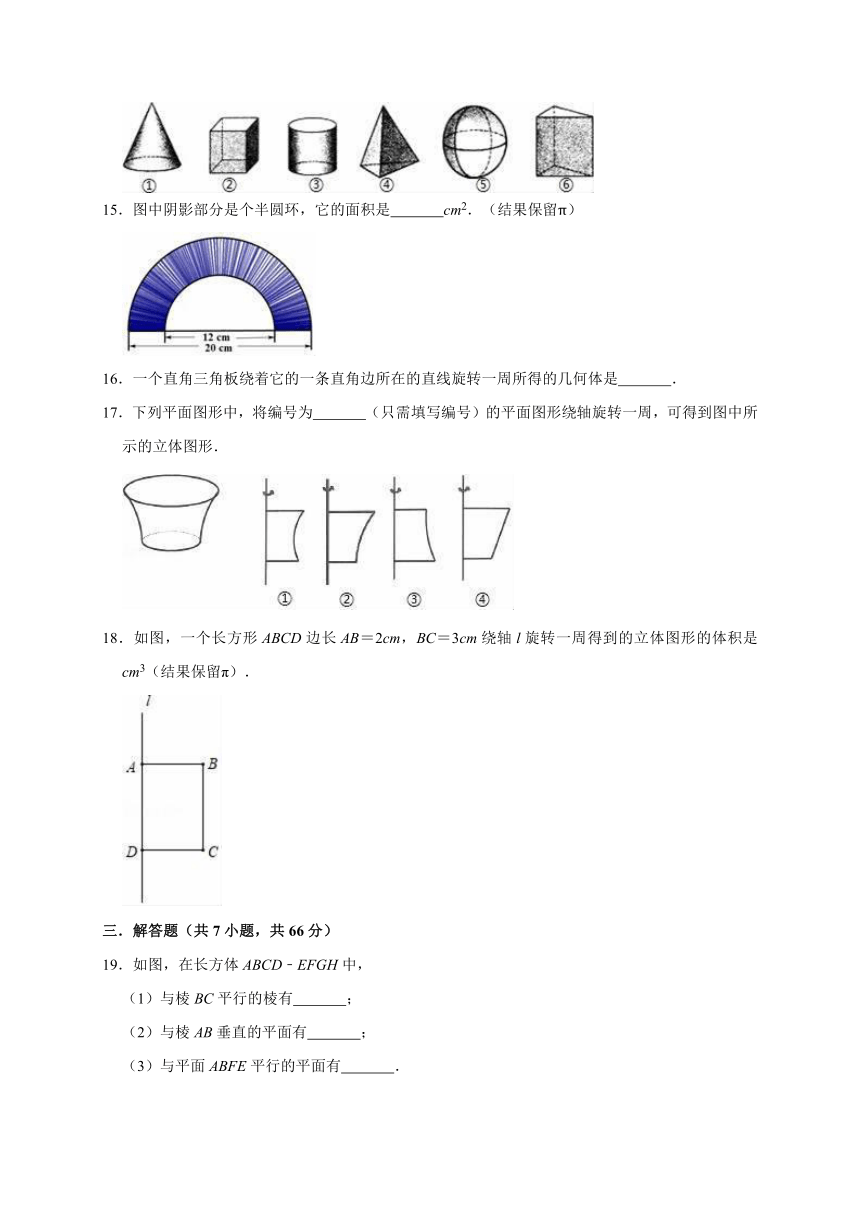
6.如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是( )
A. B. C. D.
7.“汽车上雨刷器的运动过程”能说明的数学知识是( )
A.点动成线 B.线动成面
C.面动成体 D.面与面交于线
8.把一枚硬币在桌面上竖直快速旋转后所形成的几何体是( )
A.圆柱 B.圆锥 C.球 D.正方体
9.下列哪个物体给我们以圆柱的形象( )
A. B. C. D.
10.如图,这个立体图形中小正方体的个数是( )
A.9个 B.10个 C.13个 D.12个
二.填空题(共8小题,每小题3分,共24分)
11.一个棱锥共有20条棱,那么它是 棱锥.
12.一块长、宽、高分别为5cm,4cm,3cm的长方体橡皮泥,要用它来捏一个底面半径为2cm的圆柱,设它的高是hcm,根据题意列方程为 .
13.五棱柱有 个面.
14.下列图形中,是柱体的有 .(填序号)
15.图中阴影部分是个半圆环,它的面积是 cm2.(结果保留π)
16.一个直角三角板绕着它的一条直角边所在的直线旋转一周所得的几何体是 .
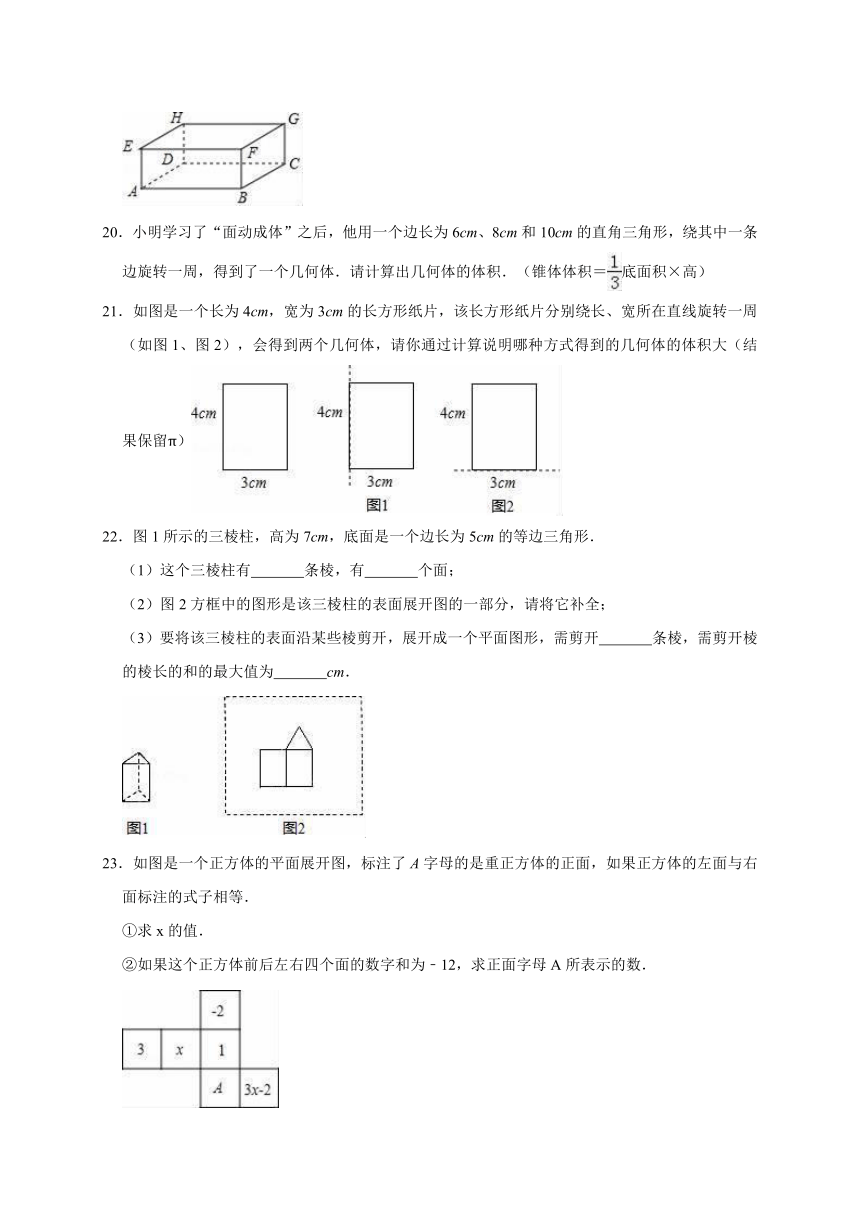
17.下列平面图形中,将编号为 (只需填写编号)的平面图形绕轴旋转一周,可得到图中所示的立体图形.
18.如图,一个长方形ABCD边长AB=2cm,BC=3cm绕轴l旋转一周得到的立体图形的体积是 cm3(结果保留π).
三.解答题(共7小题,共66分)
19.如图,在长方体ABCD﹣EFGH中,
(1)与棱BC平行的棱有 ;
(2)与棱AB垂直的平面有 ;
(3)与平面ABFE平行的平面有 .
20.小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=底面积×高)
21.如图是一个长为4cm,宽为3cm的长方形纸片,该长方形纸片分别绕长、宽所在直线旋转一周(如图1、图2),会得到两个几何体,请你通过计算说明哪种方式得到的几何体的体积大(结果保留π)
22.图1所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有 条棱,有 个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开 条棱,需剪开棱的棱长的和的最大值为 cm.
23.如图是一个正方体的平面展开图,标注了A字母的是重正方体的正面,如果正方体的左面与右面标注的式子相等.
①求x的值.
②如果这个正方体前后左右四个面的数字和为﹣12,求正面字母A所表示的数.
24.已知一个直棱柱,它有21条棱,其中一条侧棱长为20,底面各边长都为4.
(1)这是几棱柱?
(2)它有多少个面?多少个顶点?
(3)这个棱柱的所有侧面的面积之和是多少?
25.(1)如图1,已知三点A,B,C,按要求画图:画直线AB;画射线AC;画线段BC.
(2)如图2,用适当的语句表述点A,P与直线l的关系.
参考答案
一.选择题
1.【解答】解:A、该几何体为四棱柱,不符合题意;
B、该几何体为圆锥,不符合题意;
C、该几何体为三棱柱,符合题意;
D、该几何体为圆柱,不符合题意.
故选:C.
2.【解答】解:根据题意得:只要有一个面是曲面且是立体图形都符合题意,故含有曲面的是圆锥、球.
故选:C.
3.【解答】解:此几何体有6条棱,
故选:D.
4.【解答】解:根据图形可得组成这个标志的几何图形有长方形、圆.
故选:A.
5.【解答】解:A、球、圆锥是立体图形,错误;
B、棱锥、棱柱是立体图形,错误;
C、角、三角形、正方形、圆是平面图形,正确;
D、长方体是立体图形,错误;
故选:C.
6.【解答】解:面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,
那么所求的图形是下面是圆锥,上面是圆柱的组合图形.
故选:D.
7.【解答】解:汽车的雨刷把玻璃上的雨水刷干净,是运用了线动成面的原理,
故选:B.
8.【解答】解:把一枚硬币在桌面上竖直快速旋转后所形成的几何体是球,
故选:C.
9.【解答】解:A.此物体给我们以圆锥的形象;
B.此物体给我们以正方体的形象;
C.此物体给我们以圆柱的形象;
D.此物体给我们以球的形象;
故选:C.
10.【解答】解:由图可得,第一层有7个;第二层有5个;第三层有1个,
故这个立体图形中小正方体的个数是13个,
故选:C.
二.填空题
11.【解答】解:如果一棱锥有20条棱,那么这个棱锥是十棱锥.
故答案为:十.
12.【解答】解:根据等量关系列方程得:3×4×5=4πh,
故答案为:3×4×5=4πh.
13.【解答】解:∵五棱柱有2个底面,5个侧面,
∴五棱柱的面数为7.
故答案为:7.
14.【解答】解:①是圆锥,②是正方体,属于棱柱,③是圆柱,④是棱锥,⑤是球,⑥是三棱柱.
所以是柱体的有②③⑥.
15.【解答】解:π×[(20÷2)2﹣(12÷2)2]÷2
=π×(100﹣36)÷2
=32π(cm2).
答:它的面积是32πcm2.
故答案为:32π.
16.【解答】解:将直角三角形绕其一条直角边所在的直线旋转一周,所得的几何体是圆锥,
故答案为:圆锥.
17.【解答】解:①是两个圆台,故①错误;
②上面大下面小,侧面是曲面,故②正确;
③上面小下面大,侧面是曲面,故③错误;
④是一个圆台,故④错误;
故答案为:②.
18.【解答】解:一个长方形绕轴l旋转一周得到的立体图形是圆柱.
圆柱的体积=π×22×3=12πcm3,
故答案为:12π
三.解答题
19.【解答】解:(1)与棱BC平行的棱有AD,EH,FG;
(2)与棱AB垂直的平面有平面ADHE和平面BCGF;
(3)与平面ABFE平行的平面有平面DCGH;
故答案为:AD,EH,FG;平面ADHE和平面BCGF;平面DCGH.
20.【解答】解:以8cm为轴,得
以8cm为轴体积为×π×62×8=96π(cm3),
以6cm为轴,得
以6cm为轴的体积为×π×82×6=128π(cm3),
以10cm为轴,得
以10cm为轴的体积为×π()2×10=76.8π(cm3).
故几何体的体积为:96πcm3或128πcm3或76.8πcm3.
21.【解答】解:如图1,绕长边旋转得到的圆柱的底面半径为3cm,高为4cm,体积=π×32×4=36πcm3;
如图2,绕短边旋转得到的圆柱底面半径为4cm,高为3cm,体积=π×42×3=48πcm3.
因此绕短边旋转得到的圆柱体积大.
22.【解答】解:(1)这个三棱柱有条9棱,有个5面;
故答案为:9,5;
(2)如图;
(3)由图形可知:没有剪开的棱的条数是4条,
则至少需要剪开的棱的条数是:9﹣4=5(条).
故至少需要剪开的棱的条数是5条.
需剪开棱的棱长的和的最大值为:7×3+5×2=31(cm).
故答案为:5,31.
23.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“A”与“﹣2”是相对面,
“3”与“1”是相对面,
“x”与“3x﹣2”是相对面,
(1)∵正方体的左面与右面标注的式子相等,
∴x=3x﹣2,
解得x=1.
(2)正方体前后左右四个面的文字分别是:A、﹣2、x、3x﹣2,
依题意得A﹣2+x+3x﹣2=﹣12
A﹣2+1+3﹣2=﹣12
A=﹣12.
24.【解答】解:(1)∵此直棱柱有21条棱,
∴由21÷3=7知,此棱柱是七棱柱;
(2)这个七棱柱有9个面,有14个顶点;
(3)这个棱柱的所有侧面的面积之和是4×7×20=560.
25.【解答】解:(1)如图所示:
(2)点A在直线l上,点P在直线l外.
一.选择题(共10小题,每小题3分,共30分)
1.下列四个几何体中,是三棱柱的为( )
A. B.
C. D.
2.如图图中,含有曲面的几何体编号( )
A.①② B.①③ C.②③ D.②④
3.图中的几何体有( )条棱.
A.3 B.4 C.5 D.6
4.如图是交通禁止驶入标志,组成这个标志的几何图形有( )
A.圆、长方形 B.圆、线段 C.球、长方形 D.球、线段
5.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥 B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆 D.点、角、线段、长方体
6.如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是( )
A. B. C. D.
7.“汽车上雨刷器的运动过程”能说明的数学知识是( )
A.点动成线 B.线动成面
C.面动成体 D.面与面交于线
8.把一枚硬币在桌面上竖直快速旋转后所形成的几何体是( )
A.圆柱 B.圆锥 C.球 D.正方体
9.下列哪个物体给我们以圆柱的形象( )
A. B. C. D.
10.如图,这个立体图形中小正方体的个数是( )
A.9个 B.10个 C.13个 D.12个
二.填空题(共8小题,每小题3分,共24分)
11.一个棱锥共有20条棱,那么它是 棱锥.
12.一块长、宽、高分别为5cm,4cm,3cm的长方体橡皮泥,要用它来捏一个底面半径为2cm的圆柱,设它的高是hcm,根据题意列方程为 .
13.五棱柱有 个面.
14.下列图形中,是柱体的有 .(填序号)
15.图中阴影部分是个半圆环,它的面积是 cm2.(结果保留π)
16.一个直角三角板绕着它的一条直角边所在的直线旋转一周所得的几何体是 .
17.下列平面图形中,将编号为 (只需填写编号)的平面图形绕轴旋转一周,可得到图中所示的立体图形.
18.如图,一个长方形ABCD边长AB=2cm,BC=3cm绕轴l旋转一周得到的立体图形的体积是 cm3(结果保留π).
三.解答题(共7小题,共66分)
19.如图,在长方体ABCD﹣EFGH中,
(1)与棱BC平行的棱有 ;
(2)与棱AB垂直的平面有 ;
(3)与平面ABFE平行的平面有 .
20.小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=底面积×高)
21.如图是一个长为4cm,宽为3cm的长方形纸片,该长方形纸片分别绕长、宽所在直线旋转一周(如图1、图2),会得到两个几何体,请你通过计算说明哪种方式得到的几何体的体积大(结果保留π)
22.图1所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有 条棱,有 个面;
(2)图2方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开 条棱,需剪开棱的棱长的和的最大值为 cm.
23.如图是一个正方体的平面展开图,标注了A字母的是重正方体的正面,如果正方体的左面与右面标注的式子相等.
①求x的值.
②如果这个正方体前后左右四个面的数字和为﹣12,求正面字母A所表示的数.
24.已知一个直棱柱,它有21条棱,其中一条侧棱长为20,底面各边长都为4.
(1)这是几棱柱?
(2)它有多少个面?多少个顶点?
(3)这个棱柱的所有侧面的面积之和是多少?
25.(1)如图1,已知三点A,B,C,按要求画图:画直线AB;画射线AC;画线段BC.
(2)如图2,用适当的语句表述点A,P与直线l的关系.
参考答案
一.选择题
1.【解答】解:A、该几何体为四棱柱,不符合题意;
B、该几何体为圆锥,不符合题意;
C、该几何体为三棱柱,符合题意;
D、该几何体为圆柱,不符合题意.
故选:C.
2.【解答】解:根据题意得:只要有一个面是曲面且是立体图形都符合题意,故含有曲面的是圆锥、球.
故选:C.
3.【解答】解:此几何体有6条棱,
故选:D.
4.【解答】解:根据图形可得组成这个标志的几何图形有长方形、圆.
故选:A.
5.【解答】解:A、球、圆锥是立体图形,错误;
B、棱锥、棱柱是立体图形,错误;
C、角、三角形、正方形、圆是平面图形,正确;
D、长方体是立体图形,错误;
故选:C.
6.【解答】解:面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,
那么所求的图形是下面是圆锥,上面是圆柱的组合图形.
故选:D.
7.【解答】解:汽车的雨刷把玻璃上的雨水刷干净,是运用了线动成面的原理,
故选:B.
8.【解答】解:把一枚硬币在桌面上竖直快速旋转后所形成的几何体是球,
故选:C.
9.【解答】解:A.此物体给我们以圆锥的形象;
B.此物体给我们以正方体的形象;
C.此物体给我们以圆柱的形象;
D.此物体给我们以球的形象;
故选:C.
10.【解答】解:由图可得,第一层有7个;第二层有5个;第三层有1个,
故这个立体图形中小正方体的个数是13个,
故选:C.
二.填空题
11.【解答】解:如果一棱锥有20条棱,那么这个棱锥是十棱锥.
故答案为:十.
12.【解答】解:根据等量关系列方程得:3×4×5=4πh,
故答案为:3×4×5=4πh.
13.【解答】解:∵五棱柱有2个底面,5个侧面,
∴五棱柱的面数为7.
故答案为:7.
14.【解答】解:①是圆锥,②是正方体,属于棱柱,③是圆柱,④是棱锥,⑤是球,⑥是三棱柱.
所以是柱体的有②③⑥.
15.【解答】解:π×[(20÷2)2﹣(12÷2)2]÷2
=π×(100﹣36)÷2
=32π(cm2).
答:它的面积是32πcm2.
故答案为:32π.
16.【解答】解:将直角三角形绕其一条直角边所在的直线旋转一周,所得的几何体是圆锥,
故答案为:圆锥.
17.【解答】解:①是两个圆台,故①错误;
②上面大下面小,侧面是曲面,故②正确;
③上面小下面大,侧面是曲面,故③错误;
④是一个圆台,故④错误;
故答案为:②.
18.【解答】解:一个长方形绕轴l旋转一周得到的立体图形是圆柱.
圆柱的体积=π×22×3=12πcm3,
故答案为:12π
三.解答题
19.【解答】解:(1)与棱BC平行的棱有AD,EH,FG;
(2)与棱AB垂直的平面有平面ADHE和平面BCGF;
(3)与平面ABFE平行的平面有平面DCGH;
故答案为:AD,EH,FG;平面ADHE和平面BCGF;平面DCGH.
20.【解答】解:以8cm为轴,得
以8cm为轴体积为×π×62×8=96π(cm3),
以6cm为轴,得
以6cm为轴的体积为×π×82×6=128π(cm3),
以10cm为轴,得
以10cm为轴的体积为×π()2×10=76.8π(cm3).
故几何体的体积为:96πcm3或128πcm3或76.8πcm3.
21.【解答】解:如图1,绕长边旋转得到的圆柱的底面半径为3cm,高为4cm,体积=π×32×4=36πcm3;
如图2,绕短边旋转得到的圆柱底面半径为4cm,高为3cm,体积=π×42×3=48πcm3.
因此绕短边旋转得到的圆柱体积大.
22.【解答】解:(1)这个三棱柱有条9棱,有个5面;
故答案为:9,5;
(2)如图;
(3)由图形可知:没有剪开的棱的条数是4条,
则至少需要剪开的棱的条数是:9﹣4=5(条).
故至少需要剪开的棱的条数是5条.
需剪开棱的棱长的和的最大值为:7×3+5×2=31(cm).
故答案为:5,31.
23.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“A”与“﹣2”是相对面,
“3”与“1”是相对面,
“x”与“3x﹣2”是相对面,
(1)∵正方体的左面与右面标注的式子相等,
∴x=3x﹣2,
解得x=1.
(2)正方体前后左右四个面的文字分别是:A、﹣2、x、3x﹣2,
依题意得A﹣2+x+3x﹣2=﹣12
A﹣2+1+3﹣2=﹣12
A=﹣12.
24.【解答】解:(1)∵此直棱柱有21条棱,
∴由21÷3=7知,此棱柱是七棱柱;
(2)这个七棱柱有9个面,有14个顶点;
(3)这个棱柱的所有侧面的面积之和是4×7×20=560.
25.【解答】解:(1)如图所示:
(2)点A在直线l上,点P在直线l外.
