人教版选修2-1 2.1.1曲线与方程课件(25张)
文档属性
| 名称 | 人教版选修2-1 2.1.1曲线与方程课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 187.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-24 17:29:40 | ||
图片预览







文档简介
课件25张PPT。 《曲线与方程》知识探究1.如果点M(x0,y0)是曲线C上任意一点, 点M的坐标是方程x-y=0 的解吗? ①曲线C上的所有点的
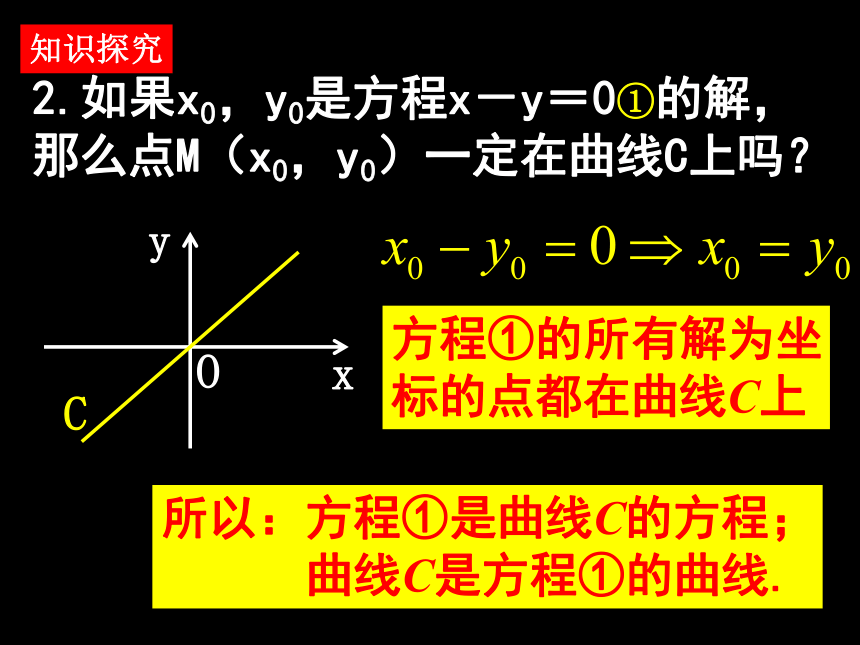
坐标都满足方程①2.如果x0,y0是方程x-y=0①的解, 那么点M(x0,y0)一定在曲线C上吗? 知识探究方程①的所有解为坐
标的点都在曲线C上所以:方程①是曲线C的方程;
曲线C是方程①的曲线.3.曲线C上的点的坐标都是方程
|x|=|y|的解吗?以方程|x|=|y|
的解为坐标的点都在曲线C上吗?知识探究4.曲线C上的点的坐标都是方程
的解吗?以方程
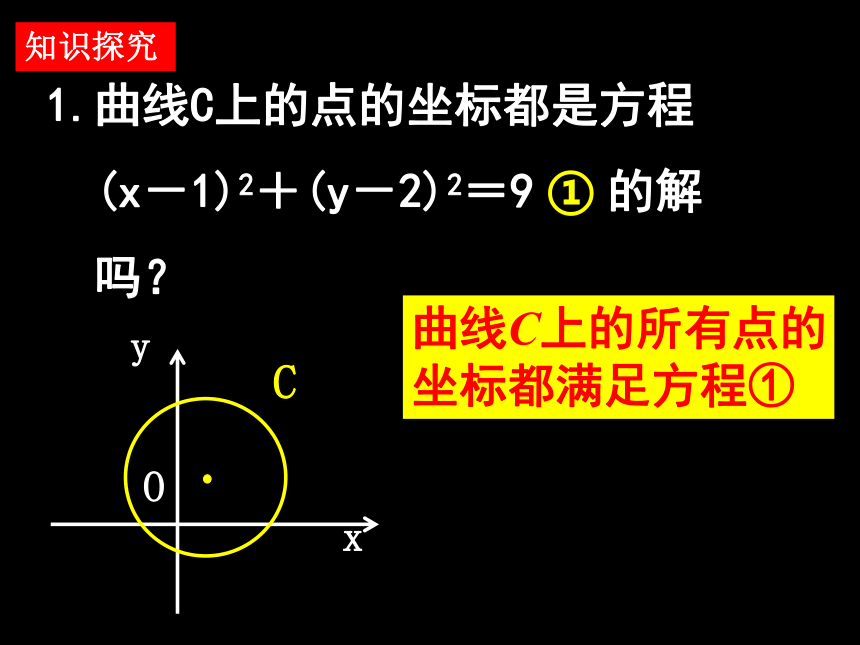
的解为坐标的点都在曲线C上吗?知识探究设曲线C表示直角坐标系中以点(1,2)为圆心,3为半径的圆.知识探究1.曲线C上的点的坐标都是方程
(x-1)2+(y-2)2=9 的解
吗?知识探究① 曲线C上的所有点的
坐标都满足方程①2.如果x0,y0是方程(x-1)2+(y-2)2=9的解,那么点M(x0,y0)一定在曲线C上吗? 知识探究以方程①的解为坐标的点都在曲线C上所以:方程①是曲线C的方程;
曲线C是方程①的曲线.知识探究3.曲线C上的点的坐标都是方程
的解吗?以这个方程的解为坐标的点都在曲线C上吗? 若曲线C与二元方程f(x,y)=0满足
(1)曲线上点的坐标都是这个方程的
解
(2)以这个方程的解为坐标的点都是
曲线上的点概念生成则称:方程是曲线C的方程;
曲线C是方程的曲线.两层意识,相互相承即:曲线上所有点的集合与此曲线的方程的解集能够一一对应概念形成1.求过原点且平分第一象限的射线的
方程.x-y=0(x≥0)新知探究2. 方程(x-1)2+(y-2)2=9(x<0)的曲线是什么?新知探究1.判断下列结论的正误并说明理由
(1)过点A(3,0)且垂直于x轴
的直线为x=3;
(2)到x轴距离为2的点的轨迹方
程为y=2;
(3)到两坐标轴距离乘积等于1
的点的轨迹方程为xy=1.对错错概念辨析|y|=2|xy|=1 (1)曲线C为过点A(1,1),B(-1,1)的
折线,方程为(x-y)(x+y)=0;2.判断图中曲线的方程是否正确概念辨析(2)曲线C是顶点在原点的抛物线,方
程为x+ =0;0xy-11-2212.判断图中曲线的方程是否正确概念辨析 (3)曲线C是Ⅰ, Ⅱ象限内到X轴,
Y轴的距离乘积为1的点集,方程y= 0xy-11-2212.判断图中曲线的方程是否正确概念辨析3.如果曲线C上的点坐标(x,y)都是方程 F(x,y)=0的解,那么( )
A、以方程F(x,y)=0的解为坐标的点都在曲线C上
B、以方程F(x,y)=0的解为坐标的点,有些不在曲线上.
C、不在曲线C上的点的坐标都不是方程 F(x,y)=0的解.
D、坐标不满足F(x,y)=0的点不在曲线C上.D概念辨析典型例题例1:已知三角形顶点 A(2,0)、B(0,1)、及C(2,3),写出AB边的中线CM的方程.5x-2y-4=0(1≤x≤2)例2 证明:与两条坐标轴的距离
的积为常数k(k>0)的点的轨迹方程是xy=±k.典型例题 A典型例题 错典型例题 错 正确其中y≤3除去点(2,0)课堂小结 1.方程的曲线与曲线的方程是两个并存的概念,我们常用方程描述曲线的数量关系,用曲线反映方程的几何性质,二者相辅相成,对立统一.课堂小结 2.方程与曲线是一种对应关系,根据已知条件求曲线的方程与通过曲线的方程研究曲线的性质,是解析几何的两个主要问题.谢谢大家!
坐标都满足方程①2.如果x0,y0是方程x-y=0①的解, 那么点M(x0,y0)一定在曲线C上吗? 知识探究方程①的所有解为坐
标的点都在曲线C上所以:方程①是曲线C的方程;
曲线C是方程①的曲线.3.曲线C上的点的坐标都是方程
|x|=|y|的解吗?以方程|x|=|y|
的解为坐标的点都在曲线C上吗?知识探究4.曲线C上的点的坐标都是方程
的解吗?以方程
的解为坐标的点都在曲线C上吗?知识探究设曲线C表示直角坐标系中以点(1,2)为圆心,3为半径的圆.知识探究1.曲线C上的点的坐标都是方程
(x-1)2+(y-2)2=9 的解
吗?知识探究① 曲线C上的所有点的
坐标都满足方程①2.如果x0,y0是方程(x-1)2+(y-2)2=9的解,那么点M(x0,y0)一定在曲线C上吗? 知识探究以方程①的解为坐标的点都在曲线C上所以:方程①是曲线C的方程;
曲线C是方程①的曲线.知识探究3.曲线C上的点的坐标都是方程
的解吗?以这个方程的解为坐标的点都在曲线C上吗? 若曲线C与二元方程f(x,y)=0满足
(1)曲线上点的坐标都是这个方程的
解
(2)以这个方程的解为坐标的点都是
曲线上的点概念生成则称:方程是曲线C的方程;
曲线C是方程的曲线.两层意识,相互相承即:曲线上所有点的集合与此曲线的方程的解集能够一一对应概念形成1.求过原点且平分第一象限的射线的
方程.x-y=0(x≥0)新知探究2. 方程(x-1)2+(y-2)2=9(x<0)的曲线是什么?新知探究1.判断下列结论的正误并说明理由
(1)过点A(3,0)且垂直于x轴
的直线为x=3;
(2)到x轴距离为2的点的轨迹方
程为y=2;
(3)到两坐标轴距离乘积等于1
的点的轨迹方程为xy=1.对错错概念辨析|y|=2|xy|=1 (1)曲线C为过点A(1,1),B(-1,1)的
折线,方程为(x-y)(x+y)=0;2.判断图中曲线的方程是否正确概念辨析(2)曲线C是顶点在原点的抛物线,方
程为x+ =0;0xy-11-2212.判断图中曲线的方程是否正确概念辨析 (3)曲线C是Ⅰ, Ⅱ象限内到X轴,
Y轴的距离乘积为1的点集,方程y= 0xy-11-2212.判断图中曲线的方程是否正确概念辨析3.如果曲线C上的点坐标(x,y)都是方程 F(x,y)=0的解,那么( )
A、以方程F(x,y)=0的解为坐标的点都在曲线C上
B、以方程F(x,y)=0的解为坐标的点,有些不在曲线上.
C、不在曲线C上的点的坐标都不是方程 F(x,y)=0的解.
D、坐标不满足F(x,y)=0的点不在曲线C上.D概念辨析典型例题例1:已知三角形顶点 A(2,0)、B(0,1)、及C(2,3),写出AB边的中线CM的方程.5x-2y-4=0(1≤x≤2)例2 证明:与两条坐标轴的距离
的积为常数k(k>0)的点的轨迹方程是xy=±k.典型例题 A典型例题 错典型例题 错 正确其中y≤3除去点(2,0)课堂小结 1.方程的曲线与曲线的方程是两个并存的概念,我们常用方程描述曲线的数量关系,用曲线反映方程的几何性质,二者相辅相成,对立统一.课堂小结 2.方程与曲线是一种对应关系,根据已知条件求曲线的方程与通过曲线的方程研究曲线的性质,是解析几何的两个主要问题.谢谢大家!
