人教版选修2-1 2.1.2求曲线的方程课件(16张)
文档属性
| 名称 | 人教版选修2-1 2.1.2求曲线的方程课件(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 513.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-24 17:25:33 | ||
图片预览






文档简介
课件16张PPT。1求曲线的方程1(1)曲线上点的坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都是曲线上的点.
那么,这个方程叫做曲线的方程;
这条曲线叫做方程的曲线.定义: 一般地,在直角坐标系中,如果某曲线C(看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:1 判断下列结论的正误并说明理由
(1)过点A(3,0)且垂直于x轴的直线为x=3
(2)到x轴距离为2的点的轨迹方程为y=2
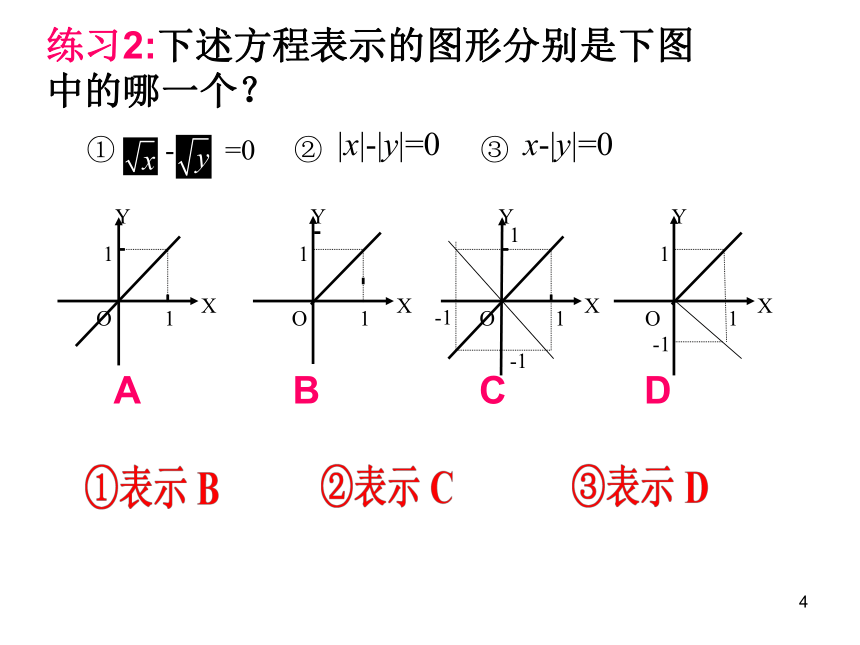
(3)到两坐标轴距离乘积等于1的点的轨迹方程为xy=1对错错练习11练习2:下述方程表示的图形分别是下图中的哪一个?11.解析几何与坐标法:
我们把借助于坐标系研究几何图形的方法叫做坐标法. 在数学中,用坐标法研究几何图形的知识形成了一门叫解析几何的学科.因此,解析几何是用代数方法研究几何问题的一门数学学科.2.平面解析几何研究的主要问题:
(1)根据已知条件,求出表示平面曲线的方程;
(2)通过方程,研究平面曲线的性质.
说明:本节主要讨论求解曲线方程的一般步骤.1111方法小结11例2.已知一条直线l和它上方的一个点A,点A到l的距离是2,一条曲线也在l的上方,它上面的每一点到A的距离减去到l的距离的差都是2,建立适当的坐标系,求这条曲线的方程.取直线l为x轴,过点A且垂直于直线l的直线为y轴,建立坐标系xOy,解:因为曲线在x轴的上方,所以y>0, 所以曲线的方程是 设点M(x,y)是曲线上任意一点,MB⊥x轴,垂足是B,1
(2)要仔细分析曲线上动点所满足的几何条件,挖掘等量关系,寻找动点坐标所适合的方程。
(3)根据具体条件,有时要注明变量X 与 Y 的变化范围。
小结:求曲线的方程要注意以下几点:
(1)当题中没给定坐标系时,我们就要适当地建立坐标系,例如题目中有两垂直直线,就可以选其做坐标轴。1直接法(轨迹法)求曲线(图形)的方程,一般有下面几个步骤:说明:一般情况下,化简前后方程的解集是相同的,步骤(5)可以省略不写,如有特殊情况,可适当予以说明.另外,根据情况,也可以省略步骤(2),直接列出曲线方程.(1)建系设点:建立适当的坐标系,用有序实数对(x,y)表示曲线上任意一点M的坐标;(2)列式:写出适合条件p的点M集合P={M|p(M)}(3)坐标化:用坐标表示条件p(M),列出方程f(x,y)=0;(4)化简:化方程f(x,y)=0为最简形式;(5)证明:说明以化简后的方程的解为坐标的点都在曲线上.(查漏除杂)注:求哪个点的轨迹,就设哪个点的坐标为(x,y)1已知平面上有两定点A,B, 平面上一动点M到A,B两点距离之比为2:1;求动点M的轨迹方程,并说出轨迹的形状。
A分析:我们要求曲线的方程肯定离不开坐标系,所以首先我们就要建立坐标系。
解:以线段AB所在的直线为x轴,线段AB的垂直平分线为y轴建立坐标系xOy。 则A(-a,0),B(a,0)。
设点M(x,y),则M属于集合
由两点间的距离公式,点M适合的条件可以表示为:
整理得:
即:
点的轨迹是以 为圆心, 为半径的圆
12.已知圆, 过原点作圆C的弦OP,求OP中点Q的轨迹方程11 作业: 动点M在曲线x2+y2=1上移动,M和定点B(3,0)连线的中点为P,求P点的轨迹方程.
11.曲线和方程反映了数形结合的思想,要充分注意化简过程的等价转换;求轨迹方程时要注意条件对变量x或y的限制。
2.求轨迹方程时,根据条件列出等式是至关重要的一环。
3.求曲线方程与求曲线的轨迹的主要区别是:求曲线的轨迹不仅要求出曲线的方程,而且还要说明和讨论所求轨迹是什么样的图形,在何处,即图形的形状、位置、大小等。
(2)以这个方程的解为坐标的点都是曲线上的点.
那么,这个方程叫做曲线的方程;
这条曲线叫做方程的曲线.定义: 一般地,在直角坐标系中,如果某曲线C(看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:1 判断下列结论的正误并说明理由
(1)过点A(3,0)且垂直于x轴的直线为x=3
(2)到x轴距离为2的点的轨迹方程为y=2
(3)到两坐标轴距离乘积等于1的点的轨迹方程为xy=1对错错练习11练习2:下述方程表示的图形分别是下图中的哪一个?11.解析几何与坐标法:
我们把借助于坐标系研究几何图形的方法叫做坐标法. 在数学中,用坐标法研究几何图形的知识形成了一门叫解析几何的学科.因此,解析几何是用代数方法研究几何问题的一门数学学科.2.平面解析几何研究的主要问题:
(1)根据已知条件,求出表示平面曲线的方程;
(2)通过方程,研究平面曲线的性质.
说明:本节主要讨论求解曲线方程的一般步骤.1111方法小结11例2.已知一条直线l和它上方的一个点A,点A到l的距离是2,一条曲线也在l的上方,它上面的每一点到A的距离减去到l的距离的差都是2,建立适当的坐标系,求这条曲线的方程.取直线l为x轴,过点A且垂直于直线l的直线为y轴,建立坐标系xOy,解:因为曲线在x轴的上方,所以y>0, 所以曲线的方程是 设点M(x,y)是曲线上任意一点,MB⊥x轴,垂足是B,1
(2)要仔细分析曲线上动点所满足的几何条件,挖掘等量关系,寻找动点坐标所适合的方程。
(3)根据具体条件,有时要注明变量X 与 Y 的变化范围。
小结:求曲线的方程要注意以下几点:
(1)当题中没给定坐标系时,我们就要适当地建立坐标系,例如题目中有两垂直直线,就可以选其做坐标轴。1直接法(轨迹法)求曲线(图形)的方程,一般有下面几个步骤:说明:一般情况下,化简前后方程的解集是相同的,步骤(5)可以省略不写,如有特殊情况,可适当予以说明.另外,根据情况,也可以省略步骤(2),直接列出曲线方程.(1)建系设点:建立适当的坐标系,用有序实数对(x,y)表示曲线上任意一点M的坐标;(2)列式:写出适合条件p的点M集合P={M|p(M)}(3)坐标化:用坐标表示条件p(M),列出方程f(x,y)=0;(4)化简:化方程f(x,y)=0为最简形式;(5)证明:说明以化简后的方程的解为坐标的点都在曲线上.(查漏除杂)注:求哪个点的轨迹,就设哪个点的坐标为(x,y)1已知平面上有两定点A,B, 平面上一动点M到A,B两点距离之比为2:1;求动点M的轨迹方程,并说出轨迹的形状。
A分析:我们要求曲线的方程肯定离不开坐标系,所以首先我们就要建立坐标系。
解:以线段AB所在的直线为x轴,线段AB的垂直平分线为y轴建立坐标系xOy。 则A(-a,0),B(a,0)。
设点M(x,y),则M属于集合
由两点间的距离公式,点M适合的条件可以表示为:
整理得:
即:
点的轨迹是以 为圆心, 为半径的圆
12.已知圆, 过原点作圆C的弦OP,求OP中点Q的轨迹方程11 作业: 动点M在曲线x2+y2=1上移动,M和定点B(3,0)连线的中点为P,求P点的轨迹方程.
11.曲线和方程反映了数形结合的思想,要充分注意化简过程的等价转换;求轨迹方程时要注意条件对变量x或y的限制。
2.求轨迹方程时,根据条件列出等式是至关重要的一环。
3.求曲线方程与求曲线的轨迹的主要区别是:求曲线的轨迹不仅要求出曲线的方程,而且还要说明和讨论所求轨迹是什么样的图形,在何处,即图形的形状、位置、大小等。
