华师大版八年级数学上册 第12章 整式的乘除 单元测试题(有详细答案)
文档属性
| 名称 | 华师大版八年级数学上册 第12章 整式的乘除 单元测试题(有详细答案) |  | |
| 格式 | zip | ||
| 文件大小 | 93.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 09:50:39 | ||
图片预览




文档简介
华师大版八年级数学上册 第12章 整式的乘除 单元测试题
一.选择题(共10小题,每小题3分,共30分)
1.计算:x3?x2等于( )
A.2 B.x5 C.2x5 D.2x6
2.下列运算止确的是( )
A.x2?x3=a6 B.(x3)2=x6
C.(﹣3x)3=27x3 D.x4+x5=x9
3.下列运算正确的是( )
A.3a×2a=6a B.(﹣a2)3?a6=a12
C.( a3)2=a9 D.(﹣m)(﹣m)4=﹣m5
4.若(x+2m)(x﹣8)中不含有x的一次项,则m的值为( )
A.4 B.﹣4 C.0 D.4或者﹣4
5.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿它的所有对称轴剪开,把它分成四块,然后按图(2)那样拼成一个正方形,则中间阴影部分的面积是( )
A.a2﹣b2 B.ab C.(a+b)2 D.(a﹣b)2
6.计算12n3÷(﹣2n)2正确的是( )
A.﹣6n B.﹣3n C.6n D.3n
7.多项式ax2﹣a与多项式ax2﹣2ax+a的公因式是( )
A.a B.x﹣1 C.a(x﹣1) D.a(x2﹣1)
8.关于x的二次三项式x2﹣ax+36能用完全平方公式分解因式,则a的值是( )
A.﹣6 B.±6 C.12 D.±12
9.若2x3﹣ax2﹣5x+5=(2x2+ax﹣1)(x﹣b)+3,其中a,b为整数,则ab的值为( )
A.2 B.﹣2 C.4 D.﹣4
10.已知a﹣2b=﹣3,那么a(a﹣4b)+4b2的值为( )
A.9 B.9 C.﹣6 D.6
二.填空题(共8小题,每小题3分。共24分)
11.已知2x=3,6x=12,则3x= .
12.已知xm=3,xn=2,则xm﹣n= .
13.计算:﹣3x2(x﹣6y)= .
14.(1+a)(a﹣1)(a2+1)= .
15.计算:﹣4a2b÷2ab= .
16.因式分解12x2y﹣15xy2= .
17.已知xy=,x﹣y=﹣3,则2x3y﹣4x2y2+2xy3= .
18.如果多项式x2﹣mx+n能因式分解为(x+2)(x﹣3),则m+n的值 .
三.解答题(共7小题,共66分)
19.(1)分解因式:2ax2﹣18a3
(2)先化简再求值:x(x﹣4y)+(2x+y)(2x﹣y)﹣(2x﹣y)2,其中x=﹣2,y=﹣1.
20.若xm=2,xn=3,求x3m﹣n的值.
21.一个长方形的长为2xcm,宽比长少4cm,若将长方形的长和宽都扩大3cm.
(1)求扩大后长方形的面积是多少?
(2)若x=2,求增大的面积为多少?
22.数学课上老师出了一题用简便方法计算2962的值,喜欢数学的小亮手做出了这道题,他的解题过程如下
2962=(300﹣4)2第一步
=3002﹣2×300×(﹣4)+42第二步
=90000+2400+16第三步
=92416第四步
老师表扬小亮积极发言的同时,也指出了解题中的错误.
(1)你认为小亮的解题过程中,从第 步开始出错.
(2)请你写出正确的解题过程.
23.对于任何实数a,b,c,d,我们规定:=ad﹣bc
(1)按照这个规定请你计算的值;
(2)按照这个规定请你计算:当x=3时,的值.
24.阅读下面文字内容:对于形如x2+2ax+a2的二次三项式,
可以直接用完全平方公式把它分解成(x+a)2的形式.但对于二次三项式x2+4x﹣5,就不能直接用完全平方公式分解了.对此,我们可以添上一项4,使它与x2+4x构成个完全平方式,然后再减去4,这样整个多项式的值不变,即x2+4x﹣5=(x2+4x+4)﹣4﹣5=(x+2)2﹣9=(x+2+3)(x+2﹣3)=(x+5)(x﹣1).像这样,把一个二次三项式变成含有完全平方式的方法,叫做配方法.
请用配方法来解下列问题
(1)请用上述方法把x2﹣6x﹣7分解因式.
(2)已知:x2+y2+4x﹣6y+13=0,求y的值.
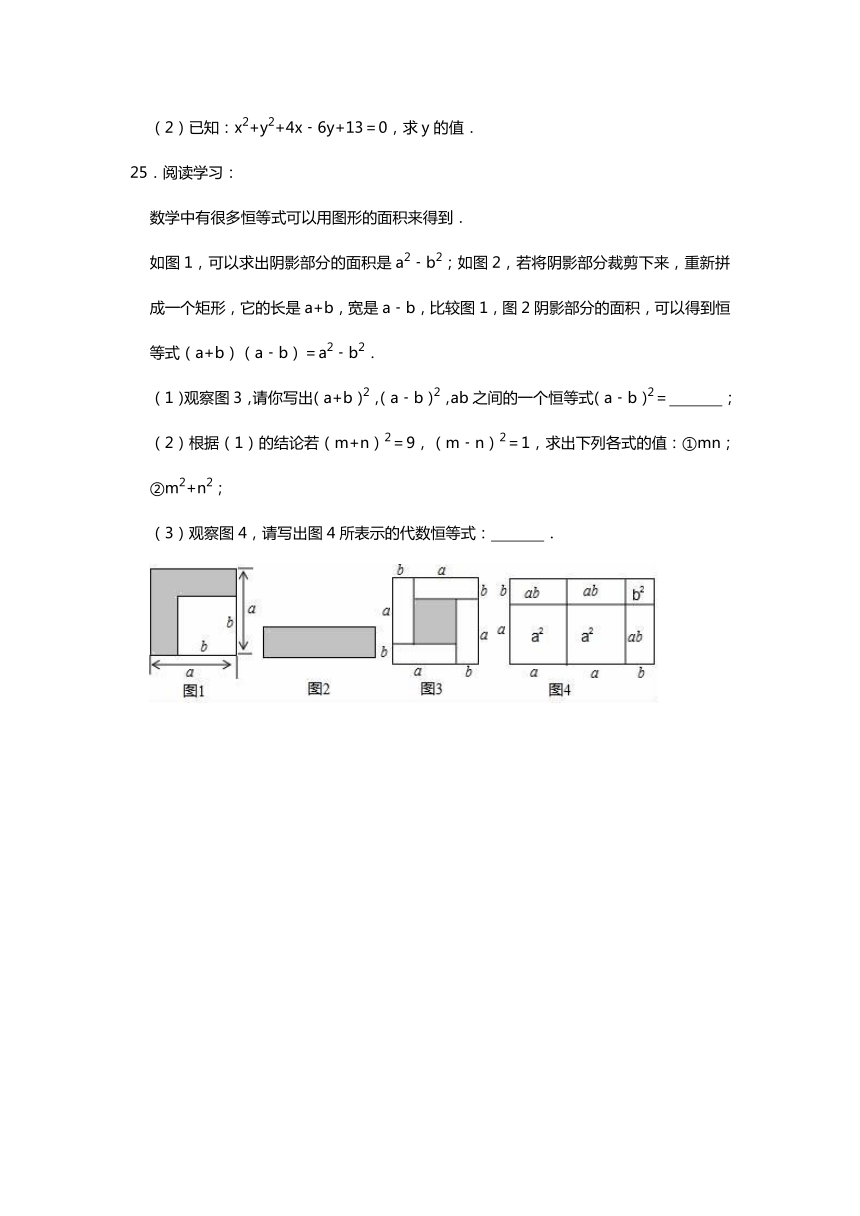
25.阅读学习:
数学中有很多恒等式可以用图形的面积来得到.
如图1,可以求出阴影部分的面积是a2﹣b2;如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的长是a+b,宽是a﹣b,比较图1,图2阴影部分的面积,可以得到恒等式(a+b)(a﹣b)=a2﹣b2.
(1)观察图3,请你写出(a+b)2,(a﹣b)2,ab之间的一个恒等式(a﹣b)2= ;
(2)根据(1)的结论若(m+n)2=9,(m﹣n)2=1,求出下列各式的值:①mn;②m2+n2;
(3)观察图4,请写出图4所表示的代数恒等式: .
参考答案
一.选择题
1.解:x3?x2=x5
故选:B.
2.解:∵x2?x3≠a6,
∴选项A不符合题意;
∵(x3)2=x6,
∴选项B符合题意;
∵(﹣3x)3=﹣27x3,
∴选项C不符合题意;
∵x4+x5≠x9,
∴选项D不符合题意.
故选:B.
3.解:(A)原式=6a2,故A错误;
(B)原式=﹣a12,故B错误;
(C)原式=a6,故C错误;
故选:D.
4.解:原式=2x2+(2m﹣8)x﹣16m,
由结果不含x的一次项,得到2m﹣8=0,
解得:m=4,
故选:A.
5.解:阴影部分的面积S=(a+b)2﹣2a?2b=a2+2ab+b2﹣4ab=(a﹣b)2,
故选:D.
6.解:12n3÷(﹣2n)2
=12n3÷4n2
=3n,
故选:D.
7.解:多项式ax2﹣a=a(x+1)(x﹣1),多项式ax2﹣2ax+a=a(x﹣1)2,
则两多项式的公因式为a(x﹣1).
故选:C.
8.解:依题意,得
ax=±2×6x,
解得:a=±12.
故选:D.
9.解:(2x2+ax﹣1)(x﹣b)+3
=2x3+(a﹣2b)x2﹣(ab+1)x+(b+3)
=2x3﹣ax2﹣5x+5,
∴a﹣2b=﹣a,
ab+1=5,
b+3=5,
∴b=2,a=2,
∴ab=4;
故选:C.
10.解:∵a﹣2b=﹣3,
∴a(a﹣4b)+4b2
=a2﹣4ab+4b2
=(a﹣2b)2
=(﹣3)2
=9
故选:B.
二.填空题
11.解:因为6x=12,
所以(2×3)x=12,
即2x×3x=12,
因为2x=3,
所以3x=12÷3=4.
故答案为:4.
12.解:∵xm=3,xn=2,
∴xm﹣n=xm÷xn=.
故答案为:.
13.解:﹣3x2(x﹣6y)=﹣3x3+18x2y,
故答案为:﹣3x3+18x2y.
14.解:原式=(a2﹣1)(a2+1)=a4﹣1,
故答案为:a4﹣1
15.解:﹣4a2b÷2ab=﹣2a.
故答案为:﹣2a.
16.解:原式=3xy(4x﹣5y).
故答案为:3xy(4x﹣5y).
17.解:∵xy=,x﹣y=﹣3,
∴2x3y﹣4x2y2+2xy3=2xy(x2﹣2xy+y2)
=2xy(x﹣y)2
=2××32
=9.
故答案为:9.
18.解:∵多项式x2﹣mx+n能因式分解为(x+2)(x﹣3),
∴x2﹣mx+n=x2﹣x﹣6,
∴m=1,n=﹣6,
∴m+n=1﹣6=﹣5.
故答案是:﹣5.
三.解答题
19.解:(1)原式=2a(x2﹣9a2)=2a(x+3a)(x﹣3a);
(2)原式=x2﹣4xy+4x2﹣y2﹣4x2+4xy﹣y2=x2﹣2y2,
当x=﹣2,y=﹣1时,原式=4﹣2=2.
20.解:x3m﹣n=x3m÷xn
=(xm)3÷xn
∵xm=2,xn=3,
∴原式=23÷3
=8÷3
=
21.解:(1)(2x+3)(2x﹣4+3)
=(2x+3)(2x﹣1)
=4x2﹣2x+6x﹣3
=4x2+4x﹣3
答:扩大后长方形的面积是(4x2+4x﹣3)cm2;
(2)(2x+3)(2x﹣4+3)﹣2x(2x﹣4),
=(2x+3)(2x﹣1)﹣4x2+8x,
=4x2﹣2x+6x﹣3﹣4x2+8x,
=12x﹣3,
面积增大了(12x﹣3)cm2;
当x=2时,12x﹣3=12×2﹣3=21;
答:增大的面积为21cm2.
22.解:(1)从第二步开始出错;
故答案为:二;
(2)正确的解题过程是:2962=(300﹣4)2
=3002﹣2×300×4+42
=90000﹣2400+16
=87616.
23.解:(1)根据题中的新定义得:原式=6×9﹣7×8=﹣2;
(2)根据题中的新定义得:原式=(x+1)(x﹣1)﹣x(x﹣2)=x2﹣1﹣x2+2x=2x﹣1,
当x=3时,原式=2x﹣1=2×3﹣1=5.
24.解:(1)x2﹣6x﹣7
=x2﹣6x+9﹣9﹣7
=(x﹣3)2﹣16
=(x﹣3﹣4)(x﹣3+4)
=(x﹣7)(x+1)
(2)∵x2+y2+4x﹣6y+13=0,
∴x2+4x+4+y2﹣6y+9=0,
∴(x+2)2+(y﹣3)2=0,
∴x+2=0,y﹣3=0,
解得x=﹣2,y=3.
25.解:(1)由图3得:(a﹣b)2=(a+b)2﹣4ab,
故答案为:(a+b)2﹣4ab;
(2)解:①根据(1)的结论,可得(m﹣n)2=(m+n)2﹣4mn,
∵(m+n)2=9,(m﹣n)2=1,
即1=9﹣4mn,
解得mn=2;
②由(m+n)2=m2+2mn+n2,可得,
9=m2+2×2+n2,
所以m2+n2=9﹣4=5;
(3)由图4得:(2a+b)(a+b)=2a2+3ab+b2.
故答案为:(2a+b)(a+b)=2a2+3ab+b2.
(注:等式2a2+3ab+b2=(2a+b)(a+b)也可得分)
一.选择题(共10小题,每小题3分,共30分)
1.计算:x3?x2等于( )
A.2 B.x5 C.2x5 D.2x6
2.下列运算止确的是( )
A.x2?x3=a6 B.(x3)2=x6
C.(﹣3x)3=27x3 D.x4+x5=x9
3.下列运算正确的是( )
A.3a×2a=6a B.(﹣a2)3?a6=a12
C.( a3)2=a9 D.(﹣m)(﹣m)4=﹣m5
4.若(x+2m)(x﹣8)中不含有x的一次项,则m的值为( )
A.4 B.﹣4 C.0 D.4或者﹣4
5.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿它的所有对称轴剪开,把它分成四块,然后按图(2)那样拼成一个正方形,则中间阴影部分的面积是( )
A.a2﹣b2 B.ab C.(a+b)2 D.(a﹣b)2
6.计算12n3÷(﹣2n)2正确的是( )
A.﹣6n B.﹣3n C.6n D.3n
7.多项式ax2﹣a与多项式ax2﹣2ax+a的公因式是( )
A.a B.x﹣1 C.a(x﹣1) D.a(x2﹣1)
8.关于x的二次三项式x2﹣ax+36能用完全平方公式分解因式,则a的值是( )
A.﹣6 B.±6 C.12 D.±12
9.若2x3﹣ax2﹣5x+5=(2x2+ax﹣1)(x﹣b)+3,其中a,b为整数,则ab的值为( )
A.2 B.﹣2 C.4 D.﹣4
10.已知a﹣2b=﹣3,那么a(a﹣4b)+4b2的值为( )
A.9 B.9 C.﹣6 D.6
二.填空题(共8小题,每小题3分。共24分)
11.已知2x=3,6x=12,则3x= .
12.已知xm=3,xn=2,则xm﹣n= .
13.计算:﹣3x2(x﹣6y)= .
14.(1+a)(a﹣1)(a2+1)= .
15.计算:﹣4a2b÷2ab= .
16.因式分解12x2y﹣15xy2= .
17.已知xy=,x﹣y=﹣3,则2x3y﹣4x2y2+2xy3= .
18.如果多项式x2﹣mx+n能因式分解为(x+2)(x﹣3),则m+n的值 .
三.解答题(共7小题,共66分)
19.(1)分解因式:2ax2﹣18a3
(2)先化简再求值:x(x﹣4y)+(2x+y)(2x﹣y)﹣(2x﹣y)2,其中x=﹣2,y=﹣1.
20.若xm=2,xn=3,求x3m﹣n的值.
21.一个长方形的长为2xcm,宽比长少4cm,若将长方形的长和宽都扩大3cm.
(1)求扩大后长方形的面积是多少?
(2)若x=2,求增大的面积为多少?
22.数学课上老师出了一题用简便方法计算2962的值,喜欢数学的小亮手做出了这道题,他的解题过程如下
2962=(300﹣4)2第一步
=3002﹣2×300×(﹣4)+42第二步
=90000+2400+16第三步
=92416第四步
老师表扬小亮积极发言的同时,也指出了解题中的错误.
(1)你认为小亮的解题过程中,从第 步开始出错.
(2)请你写出正确的解题过程.
23.对于任何实数a,b,c,d,我们规定:=ad﹣bc
(1)按照这个规定请你计算的值;
(2)按照这个规定请你计算:当x=3时,的值.
24.阅读下面文字内容:对于形如x2+2ax+a2的二次三项式,
可以直接用完全平方公式把它分解成(x+a)2的形式.但对于二次三项式x2+4x﹣5,就不能直接用完全平方公式分解了.对此,我们可以添上一项4,使它与x2+4x构成个完全平方式,然后再减去4,这样整个多项式的值不变,即x2+4x﹣5=(x2+4x+4)﹣4﹣5=(x+2)2﹣9=(x+2+3)(x+2﹣3)=(x+5)(x﹣1).像这样,把一个二次三项式变成含有完全平方式的方法,叫做配方法.
请用配方法来解下列问题
(1)请用上述方法把x2﹣6x﹣7分解因式.
(2)已知:x2+y2+4x﹣6y+13=0,求y的值.
25.阅读学习:
数学中有很多恒等式可以用图形的面积来得到.
如图1,可以求出阴影部分的面积是a2﹣b2;如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的长是a+b,宽是a﹣b,比较图1,图2阴影部分的面积,可以得到恒等式(a+b)(a﹣b)=a2﹣b2.
(1)观察图3,请你写出(a+b)2,(a﹣b)2,ab之间的一个恒等式(a﹣b)2= ;
(2)根据(1)的结论若(m+n)2=9,(m﹣n)2=1,求出下列各式的值:①mn;②m2+n2;
(3)观察图4,请写出图4所表示的代数恒等式: .
参考答案
一.选择题
1.解:x3?x2=x5
故选:B.
2.解:∵x2?x3≠a6,
∴选项A不符合题意;
∵(x3)2=x6,
∴选项B符合题意;
∵(﹣3x)3=﹣27x3,
∴选项C不符合题意;
∵x4+x5≠x9,
∴选项D不符合题意.
故选:B.
3.解:(A)原式=6a2,故A错误;
(B)原式=﹣a12,故B错误;
(C)原式=a6,故C错误;
故选:D.
4.解:原式=2x2+(2m﹣8)x﹣16m,
由结果不含x的一次项,得到2m﹣8=0,
解得:m=4,
故选:A.
5.解:阴影部分的面积S=(a+b)2﹣2a?2b=a2+2ab+b2﹣4ab=(a﹣b)2,
故选:D.
6.解:12n3÷(﹣2n)2
=12n3÷4n2
=3n,
故选:D.
7.解:多项式ax2﹣a=a(x+1)(x﹣1),多项式ax2﹣2ax+a=a(x﹣1)2,
则两多项式的公因式为a(x﹣1).
故选:C.
8.解:依题意,得
ax=±2×6x,
解得:a=±12.
故选:D.
9.解:(2x2+ax﹣1)(x﹣b)+3
=2x3+(a﹣2b)x2﹣(ab+1)x+(b+3)
=2x3﹣ax2﹣5x+5,
∴a﹣2b=﹣a,
ab+1=5,
b+3=5,
∴b=2,a=2,
∴ab=4;
故选:C.
10.解:∵a﹣2b=﹣3,
∴a(a﹣4b)+4b2
=a2﹣4ab+4b2
=(a﹣2b)2
=(﹣3)2
=9
故选:B.
二.填空题
11.解:因为6x=12,
所以(2×3)x=12,
即2x×3x=12,
因为2x=3,
所以3x=12÷3=4.
故答案为:4.
12.解:∵xm=3,xn=2,
∴xm﹣n=xm÷xn=.
故答案为:.
13.解:﹣3x2(x﹣6y)=﹣3x3+18x2y,
故答案为:﹣3x3+18x2y.
14.解:原式=(a2﹣1)(a2+1)=a4﹣1,
故答案为:a4﹣1
15.解:﹣4a2b÷2ab=﹣2a.
故答案为:﹣2a.
16.解:原式=3xy(4x﹣5y).
故答案为:3xy(4x﹣5y).
17.解:∵xy=,x﹣y=﹣3,
∴2x3y﹣4x2y2+2xy3=2xy(x2﹣2xy+y2)
=2xy(x﹣y)2
=2××32
=9.
故答案为:9.
18.解:∵多项式x2﹣mx+n能因式分解为(x+2)(x﹣3),
∴x2﹣mx+n=x2﹣x﹣6,
∴m=1,n=﹣6,
∴m+n=1﹣6=﹣5.
故答案是:﹣5.
三.解答题
19.解:(1)原式=2a(x2﹣9a2)=2a(x+3a)(x﹣3a);
(2)原式=x2﹣4xy+4x2﹣y2﹣4x2+4xy﹣y2=x2﹣2y2,
当x=﹣2,y=﹣1时,原式=4﹣2=2.
20.解:x3m﹣n=x3m÷xn
=(xm)3÷xn
∵xm=2,xn=3,
∴原式=23÷3
=8÷3
=
21.解:(1)(2x+3)(2x﹣4+3)
=(2x+3)(2x﹣1)
=4x2﹣2x+6x﹣3
=4x2+4x﹣3
答:扩大后长方形的面积是(4x2+4x﹣3)cm2;
(2)(2x+3)(2x﹣4+3)﹣2x(2x﹣4),
=(2x+3)(2x﹣1)﹣4x2+8x,
=4x2﹣2x+6x﹣3﹣4x2+8x,
=12x﹣3,
面积增大了(12x﹣3)cm2;
当x=2时,12x﹣3=12×2﹣3=21;
答:增大的面积为21cm2.
22.解:(1)从第二步开始出错;
故答案为:二;
(2)正确的解题过程是:2962=(300﹣4)2
=3002﹣2×300×4+42
=90000﹣2400+16
=87616.
23.解:(1)根据题中的新定义得:原式=6×9﹣7×8=﹣2;
(2)根据题中的新定义得:原式=(x+1)(x﹣1)﹣x(x﹣2)=x2﹣1﹣x2+2x=2x﹣1,
当x=3时,原式=2x﹣1=2×3﹣1=5.
24.解:(1)x2﹣6x﹣7
=x2﹣6x+9﹣9﹣7
=(x﹣3)2﹣16
=(x﹣3﹣4)(x﹣3+4)
=(x﹣7)(x+1)
(2)∵x2+y2+4x﹣6y+13=0,
∴x2+4x+4+y2﹣6y+9=0,
∴(x+2)2+(y﹣3)2=0,
∴x+2=0,y﹣3=0,
解得x=﹣2,y=3.
25.解:(1)由图3得:(a﹣b)2=(a+b)2﹣4ab,
故答案为:(a+b)2﹣4ab;
(2)解:①根据(1)的结论,可得(m﹣n)2=(m+n)2﹣4mn,
∵(m+n)2=9,(m﹣n)2=1,
即1=9﹣4mn,
解得mn=2;
②由(m+n)2=m2+2mn+n2,可得,
9=m2+2×2+n2,
所以m2+n2=9﹣4=5;
(3)由图4得:(2a+b)(a+b)=2a2+3ab+b2.
故答案为:(2a+b)(a+b)=2a2+3ab+b2.
(注:等式2a2+3ab+b2=(2a+b)(a+b)也可得分)
