人教版八年级数学上册第11章三角形11.3多边形及其内角和同步测试(有答案)
文档属性
| 名称 | 人教版八年级数学上册第11章三角形11.3多边形及其内角和同步测试(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 160.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 10:36:25 | ||
图片预览


文档简介
人教版八年级数学上册 第11章 三角形 11.3 多边形及其内角和 同步测试
一.选择题(共10小题,每小题3分,共30分)
1.下列选项中的图形,不是凸多边形的是( )
A. B.
C. D.
2.在四边形ABCD中,边AB的对边是( )
A.BC B.AC C.BD D.CD
3.将一个四边形截去一个角后,它不可能是( )
A.六边形 B.五边形 C.四边形 D.三角形
4.从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成( )个三角形.
A.6 B.5 C.8 D.7
5.六边形的内角和是( )
A.900° B.720° C.540° D.360°
6.一个多边形的内角和与外角和相等,则这个多边形的边数为( )
A.8 B.6 C.5 D.4
7.若四边形ABCD中,∠A:∠B:∠C=1:2:5,且∠C=150°,则∠D的度数为( )
A.90° B.105° C.120° D.135°
8.下列邮票的多边形中,内角和等于540°的是( )
A. B.
C. D.
9.一个正n边形的每一个外角都是45°,则n=( )
A.7 B.8 C.9 D.10
10.已知一个多边形的内角和与一个外角的和是1160度,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
二.填空题(共8小题,每小题3分,共24分)
11.一个四边形截去一个角后所形成的多边形为 .
12.如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出 个三角形.
13.如图,若集合A表示四边形,集合B表示正多边形,则阴影部分表示 .
14.若一个九边形8个外角的和为200°,则它的第9个外角为 度.
15.若一个多边形的边数为8,则这个多边形的内角和为 .
16.如图是一个窗户造型,为正八边形,则∠1= °.
17.一个多边形的外角和是内角和的倍,这个多边形的边数是 .
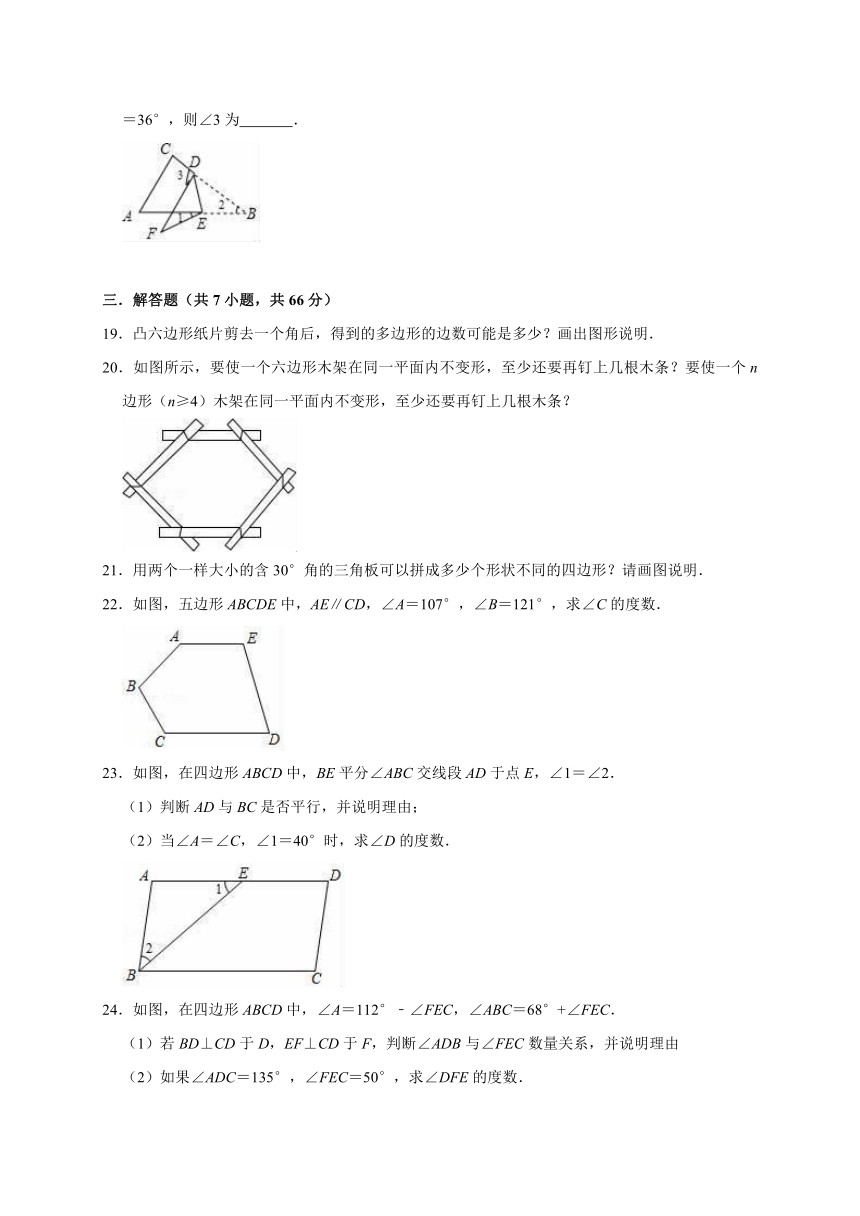
18.如图,把△ABC纸片沿DE折叠,当点B落在四边形ACDE的外部点F时,若∠1=20°,∠2=36°,则∠3为 .
三.解答题(共7小题,共66分)
19.凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
20.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条?
21.用两个一样大小的含30°角的三角板可以拼成多少个形状不同的四边形?请画图说明.
22.如图,五边形ABCDE中,AE∥CD,∠A=107°,∠B=121°,求∠C的度数.
23.如图,在四边形ABCD中,BE平分∠ABC交线段AD于点E,∠1=∠2.
(1)判断AD与BC是否平行,并说明理由;
(2)当∠A=∠C,∠1=40°时,求∠D的度数.
24.如图,在四边形ABCD中,∠A=112°﹣∠FEC,∠ABC=68°+∠FEC.
(1)若BD⊥CD于D,EF⊥CD于F,判断∠ADB与∠FEC数量关系,并说明理由
(2)如果∠ADC=135°,∠FEC=50°,求∠DFE的度数.
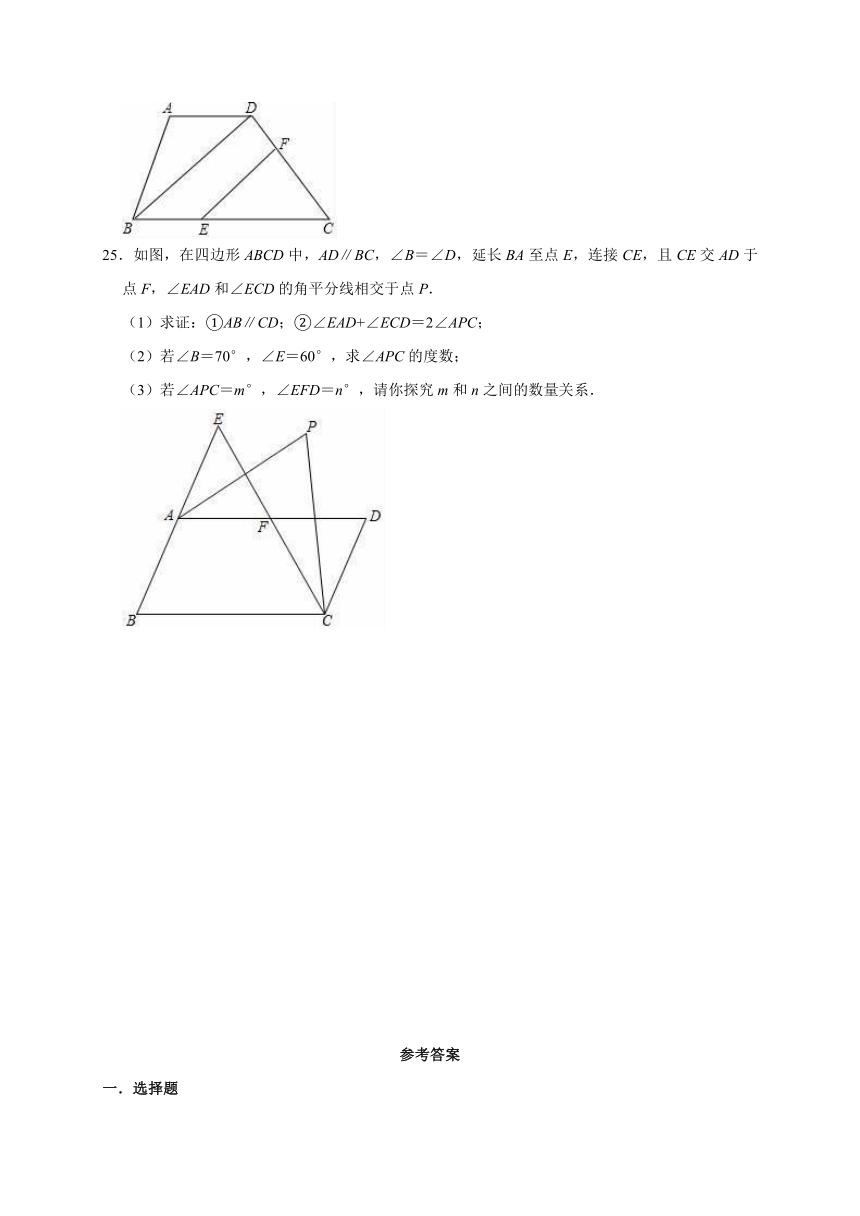
25.如图,在四边形ABCD中,AD∥BC,∠B=∠D,延长BA至点E,连接CE,且CE交AD于点F,∠EAD和∠ECD的角平分线相交于点P.
(1)求证:①AB∥CD;②∠EAD+∠ECD=2∠APC;
(2)若∠B=70°,∠E=60°,求∠APC的度数;
(3)若∠APC=m°,∠EFD=n°,请你探究m和n之间的数量关系.
参考答案
一.选择题
1. A.2. D.3. A.4. B.5. B.6. D.7. C.8. B.9. B.10. D.
二.填空题
11.三角形或四边形或五边形.12.(n﹣1).13.正方形.14. 160.
15. 1080°16. 45.17. 7.18. 92°.
三.解答题
19.【解答】解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,
∴新多边形的边数为7、5、6三种情况,
如图:
20.【解答】解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上3根木条;
要使一个n边形木架不变形,至少再钉上(n﹣3)根木条.
21.【解答】解:四个.如图所示:
22.【解答】解:过点B在B的右侧作BF∥AE.
∵BF∥AE,∠A=107°,
∴∠ABF=180°﹣107°=73°,
∵∠B=121°,
∴∠FBC=121°﹣∠ABF=48°,
又AE∥CD,BF∥AE,
∴BF∥CD,
∴∠C=180°﹣∠FBC=132°.
23.【解答】解:(1)AD∥BC,理由是:
因为BE平分∠ABC,
所以∠EBC=∠2,
因为∠1=∠2,
所以∠1=∠EBC,
所以AD∥BC(内错角相等,两直线平行);
(2)因为∠1=40°,∠1=∠2,
所以∠EBC=∠2=40°,
∠A=180°﹣∠1﹣∠2=100°,
因为∠A=∠C,
所以∠C=∠A=100°,
所以∠D=360°﹣∠A﹣∠2﹣∠EBC﹣∠C
=360°﹣100°﹣40°﹣40°﹣100°
=80°.
24.【解答】解:(1)∠ADB=∠FEC.理由如下:
∵∠A=112°﹣∠FEC,∠ABC=68°+∠FEC
∴∠A+∠ABC=112°﹣∠FEC+68°+∠FEC=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠ADB=∠DBC(两直线平行,内错角相等),
∵BD⊥DC,EF⊥DC,
∴BD∥EF(垂直于同一直线的两直线平行),
∴∠FEC=∠DBC(两直线平行,同位角相等),
∴∠ADB=∠FEC.
(2)∵∠A=112°﹣∠FEC,∠ABC=68°+∠FEC,∠FEC=50°
∴∠A+∠ABC=180°,
∴AD∥BC
∴∠ADC+∠C=180°
∴∠C=180°﹣∠ADC=45°
∵∠FEC=50°
∴∠DFE=∠C+∠FEC=95°.
25.【解答】解:(1)证明:①∵AD∥BC,∴∠EAD=∠B,
∵∠B=∠D,∴∠EAD=∠D,
∴AB∥CD;
②过点P作PQ∥AB,则∠EAP=∠APQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵∠EAP=∠EAD,∠DCP=,
∴;
(2)由(1)知AD∥BC,AB∥CD,
∴∠EAD=∠B=70°,∠ECD=∠E=60°,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠APC=;
(3)过点F作FH∥AB,则∠EAD=∠AFH,
∵AB∥CD,
∴FH∥CD,
∴∠ECD=∠CFH,
∴∠EAD+∠ECD=∠AFH+∠CFH=∠AFC=∠EFD,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠EFD=2∠APC,
∵∠APC=m°,∠EFD=n°,
∴.
一.选择题(共10小题,每小题3分,共30分)
1.下列选项中的图形,不是凸多边形的是( )
A. B.
C. D.
2.在四边形ABCD中,边AB的对边是( )
A.BC B.AC C.BD D.CD
3.将一个四边形截去一个角后,它不可能是( )
A.六边形 B.五边形 C.四边形 D.三角形
4.从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成( )个三角形.
A.6 B.5 C.8 D.7
5.六边形的内角和是( )
A.900° B.720° C.540° D.360°
6.一个多边形的内角和与外角和相等,则这个多边形的边数为( )
A.8 B.6 C.5 D.4
7.若四边形ABCD中,∠A:∠B:∠C=1:2:5,且∠C=150°,则∠D的度数为( )
A.90° B.105° C.120° D.135°
8.下列邮票的多边形中,内角和等于540°的是( )
A. B.
C. D.
9.一个正n边形的每一个外角都是45°,则n=( )
A.7 B.8 C.9 D.10
10.已知一个多边形的内角和与一个外角的和是1160度,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
二.填空题(共8小题,每小题3分,共24分)
11.一个四边形截去一个角后所形成的多边形为 .
12.如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出 个三角形.
13.如图,若集合A表示四边形,集合B表示正多边形,则阴影部分表示 .
14.若一个九边形8个外角的和为200°,则它的第9个外角为 度.
15.若一个多边形的边数为8,则这个多边形的内角和为 .
16.如图是一个窗户造型,为正八边形,则∠1= °.
17.一个多边形的外角和是内角和的倍,这个多边形的边数是 .
18.如图,把△ABC纸片沿DE折叠,当点B落在四边形ACDE的外部点F时,若∠1=20°,∠2=36°,则∠3为 .
三.解答题(共7小题,共66分)
19.凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
20.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条?
21.用两个一样大小的含30°角的三角板可以拼成多少个形状不同的四边形?请画图说明.
22.如图,五边形ABCDE中,AE∥CD,∠A=107°,∠B=121°,求∠C的度数.
23.如图,在四边形ABCD中,BE平分∠ABC交线段AD于点E,∠1=∠2.
(1)判断AD与BC是否平行,并说明理由;
(2)当∠A=∠C,∠1=40°时,求∠D的度数.
24.如图,在四边形ABCD中,∠A=112°﹣∠FEC,∠ABC=68°+∠FEC.
(1)若BD⊥CD于D,EF⊥CD于F,判断∠ADB与∠FEC数量关系,并说明理由
(2)如果∠ADC=135°,∠FEC=50°,求∠DFE的度数.
25.如图,在四边形ABCD中,AD∥BC,∠B=∠D,延长BA至点E,连接CE,且CE交AD于点F,∠EAD和∠ECD的角平分线相交于点P.
(1)求证:①AB∥CD;②∠EAD+∠ECD=2∠APC;
(2)若∠B=70°,∠E=60°,求∠APC的度数;
(3)若∠APC=m°,∠EFD=n°,请你探究m和n之间的数量关系.
参考答案
一.选择题
1. A.2. D.3. A.4. B.5. B.6. D.7. C.8. B.9. B.10. D.
二.填空题
11.三角形或四边形或五边形.12.(n﹣1).13.正方形.14. 160.
15. 1080°16. 45.17. 7.18. 92°.
三.解答题
19.【解答】解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,
∴新多边形的边数为7、5、6三种情况,
如图:
20.【解答】解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上3根木条;
要使一个n边形木架不变形,至少再钉上(n﹣3)根木条.
21.【解答】解:四个.如图所示:
22.【解答】解:过点B在B的右侧作BF∥AE.
∵BF∥AE,∠A=107°,
∴∠ABF=180°﹣107°=73°,
∵∠B=121°,
∴∠FBC=121°﹣∠ABF=48°,
又AE∥CD,BF∥AE,
∴BF∥CD,
∴∠C=180°﹣∠FBC=132°.
23.【解答】解:(1)AD∥BC,理由是:
因为BE平分∠ABC,
所以∠EBC=∠2,
因为∠1=∠2,
所以∠1=∠EBC,
所以AD∥BC(内错角相等,两直线平行);
(2)因为∠1=40°,∠1=∠2,
所以∠EBC=∠2=40°,
∠A=180°﹣∠1﹣∠2=100°,
因为∠A=∠C,
所以∠C=∠A=100°,
所以∠D=360°﹣∠A﹣∠2﹣∠EBC﹣∠C
=360°﹣100°﹣40°﹣40°﹣100°
=80°.
24.【解答】解:(1)∠ADB=∠FEC.理由如下:
∵∠A=112°﹣∠FEC,∠ABC=68°+∠FEC
∴∠A+∠ABC=112°﹣∠FEC+68°+∠FEC=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠ADB=∠DBC(两直线平行,内错角相等),
∵BD⊥DC,EF⊥DC,
∴BD∥EF(垂直于同一直线的两直线平行),
∴∠FEC=∠DBC(两直线平行,同位角相等),
∴∠ADB=∠FEC.
(2)∵∠A=112°﹣∠FEC,∠ABC=68°+∠FEC,∠FEC=50°
∴∠A+∠ABC=180°,
∴AD∥BC
∴∠ADC+∠C=180°
∴∠C=180°﹣∠ADC=45°
∵∠FEC=50°
∴∠DFE=∠C+∠FEC=95°.
25.【解答】解:(1)证明:①∵AD∥BC,∴∠EAD=∠B,
∵∠B=∠D,∴∠EAD=∠D,
∴AB∥CD;
②过点P作PQ∥AB,则∠EAP=∠APQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵AB∥CD,
∴PQ∥CD,
∴∠DCP=∠CPQ,
∵∠EAP=∠EAD,∠DCP=,
∴;
(2)由(1)知AD∥BC,AB∥CD,
∴∠EAD=∠B=70°,∠ECD=∠E=60°,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠APC=;
(3)过点F作FH∥AB,则∠EAD=∠AFH,
∵AB∥CD,
∴FH∥CD,
∴∠ECD=∠CFH,
∴∠EAD+∠ECD=∠AFH+∠CFH=∠AFC=∠EFD,
由(1)知∠EAD+∠ECD=2∠APC,
∴∠EFD=2∠APC,
∵∠APC=m°,∠EFD=n°,
∴.
