人教版八年级数学上册第12章全等三角形 12.2全等三角形的判定同步测试(有详细答案)
文档属性
| 名称 | 人教版八年级数学上册第12章全等三角形 12.2全等三角形的判定同步测试(有详细答案) |  | |
| 格式 | zip | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 10:45:38 | ||
图片预览




文档简介
人教版八年级数学上册 第12章 全等三角形 12.2 全等三角形的判定 同步测试
一.选择题(共10小题,每小题3分,共30分)
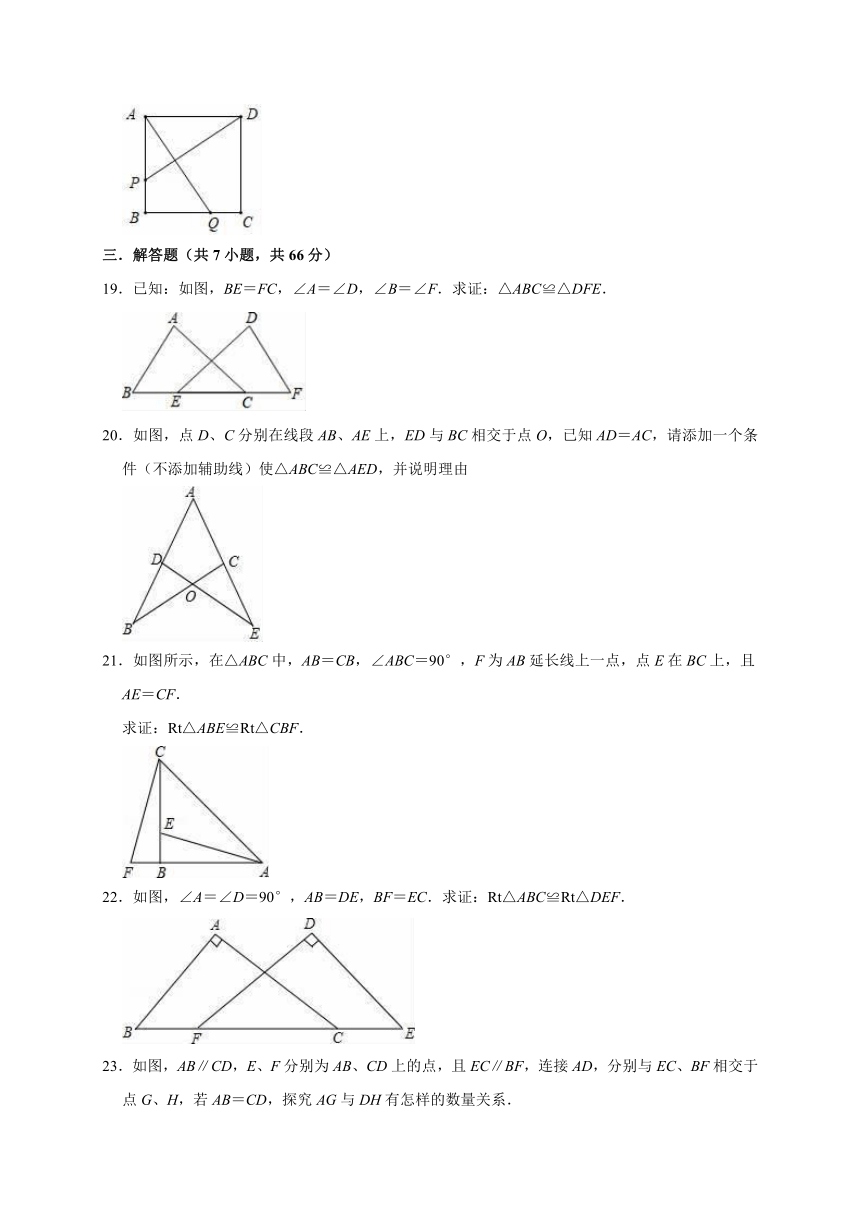
1.如图,DE⊥AC,BF⊥AC,垂足分别是E,F,且DE=BF,若利用“HL”证明△DEC≌△BFA,则需添加的条件是( )
A.EC=FA B.DC=BA C.∠D=∠B D.∠DCE=∠BAF
2.如图,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠CAP=∠APQ,PR=PS.下列结论:其中结论正确的序号是( )
①AS=AR;
②QP∥AR;
③△BRP≌△CSP
A.①② B.②③ C.①③ D.①②③
3.如图,点E,点F在直线AC上,DF=BE,∠AFD=∠CEB,下列条件中不能判断△ADF≌△CBE的是( )
A.∠B=∠D B.AD=CB C.AE=CF D.∠A=∠C
4.下列说法:①一个底角和一条边分别相等的两个等腰三角形全等;②底边及底边上的高分别相等的两个等腰三角形全等;③两边分别相等的两个直角三角形全等;④一个锐角和一条边分别相等的两个直角三角形全等,其中正确的个数是( )
A.1 B.2 C.3 D.4
5.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是( )
A.HL B.SAS C.ASA D.AAS
6.如图,AD是△ABC的高,AD=BD,DE=DC,∠BAC=75°,则∠DBE的度数是( )
A.10° B.15° C.30° D.45°
7.如图,点C是△ABE的BE边上一点,点F在AE上,D是BC的中点,且AB=AC=
CE,给出下列结论:①AD⊥BC;②CF⊥AE;③∠1=∠2;④AB+BD=DE.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
8.如图,AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,AE=7,BD=2,则DE的长是( )
A.7 B.5 C.3 D.2
9.如图,有一池塘,要测池塘两端A,B间的距离,可先在平地上取一个不经过池塘可以直接到达点A和B的点C,连接AC并延长至D,使CD=CA,连接BC并延长至E,使CE=CB,连接ED.若量出DE=58米,则A,B间的距离即可求.依据是( )
A.SAS B.SSS C.AAS D.ASA
10.如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
二.填空题(共8小题,每小题3分,共24分)
11.如图,AB∥CD,C是BE的中点,要想使得△ABC≌△DCE,还需要添加的条件是 (添加一个即可)
12.如图,AB⊥CF,垂足为B,AB∥DE,点E在CF上,CE=FB,AB=DE,依据以上条件可以判定△ABC≌△DEF,这种判定三角形全等的方法,可以简写为 .
13.如图,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,∠A=50°,则∠DFE= .
14.下列语句:①有一边对应相等的两个直角三角形全等;②一般三角形具有的性质,直角三角形都具有;③有两边相等的两直角三角形全等;④两直角三角形的斜边为5cm,一条直角边都为3cm,则这两个直角三角形必全等.其中正确的有 个.
15.如图所示的网格是正方形网格,点A,B,C,D均落在格点上,则∠BAC+∠ACD= °.
16.如图,是一个测量工件内槽宽的工具,点O既是AA'的中点,也是BB'的中点,若测得AB=5cm,则该内槽A'B'的宽为 cm.
17.如图,要在湖两岸A,B两点之间修建一座观赏桥,由于条件限制,无法直接测量A、B两点间的距离,于是小明想出来这样一种做法:在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使A,C,E三点在一条直线上,这时测得DE=50米,则AB= 米.
18.如图,在正方形ABCD中,AB=8厘米,如果动点P在线段AB上以2厘米/秒的速度由A点向B点运动,同时动点Q在以1厘米/秒的速度线段BC上由C点向B点运动,当点P到达B点时整个运动过程停止.设运动时间为t秒,当AQ⊥DP时,t的值为 秒.
三.解答题(共7小题,共66分)
19.已知:如图,BE=FC,∠A=∠D,∠B=∠F.求证:△ABC≌△DFE.
20.如图,点D、C分别在线段AB、AE上,ED与BC相交于点O,已知AD=AC,请添加一个条件(不添加辅助线)使△ABC≌△AED,并说明理由
21.如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
求证:Rt△ABE≌Rt△CBF.
22.如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.
23.如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G、H,若AB=CD,探究AG与DH有怎样的数量关系.
24.如图,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,∠ACB=∠DCE,点D在线段AB上(与A,B不重合),连接BE.
(1)证明:△ACD≌△BCE.
(2)若BD=2,BE=5,求AB的长.
25.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,AB∥DE,∠A=∠D,测得AB=DE.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
参考答案
一.选择题
1.【解答】解:∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°,
∵DE=BF,
∴当添加条件DC=BA时,可利用“HL”证明△DEC≌△BFA.
故选:B.
2.【解答】解:∵PR⊥AB,PS⊥AC,
∴∠PRA=∠PSA=90°,
∵AP=AP,PR=PS,
∴Rt△APR≌Rt△APS(HL),
∴AR=AS,所以①正确;
∠PAR=∠PAS,
∵∠CAP=∠APQ,
∴∠PAR=∠APQ,
∴QP∥AR,所以②正确;
在△BRP和△CSP中,因为只有∠PRB=∠PSC=90°,PR=PS,所以不能判断这两和三角形全等,所以③错误.
故选:A.
3.【解答】解:A、添加∠B=∠D,由全等三角形的判定定理ASA可以判定△ADF≌△CBE,故本选项错误.
B、添加AD=CB,由全等三角形的判定定理SSA不能判定△ADF≌△CBE,故本选项正确.
C、添加AE=CF,可以得到AF=CE,由全等三角形的判定定理SAS可以判定△ADF≌△CBE,故本选项错误.
D、添加∠A=∠C,由全等三角形的判定定理AAS可以判定△ADF≌△CBE,故本选项错误.
故选:B.
4.【解答】解:①一个底角和一条边分别相等的两个等腰三角形不一定全等;
②底边及底边上的高分别相等的两个等腰三角形全等,正确;
③两边分别相等的两个直角三角形不一定全等;
④如果在两个直角三角形中,例如:两个30°角的直角三角形,一个三角形的直角边与另一个三角形的斜边相等,这两个直角三角形肯定不全等,错误;
故选:A.
5.【解答】解:在Rt△AOB和Rt△COD中,
,
∴Rt△AOB≌Rt△COD(HL),
则如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是HL,
故选:A.
6.【解答】证明:∵AD=BD,AD⊥BC
∴∠BAD=∠ABD=45°
∵∠DAC=∠BAC﹣∠BAD
∴∠DAC=75°﹣45°=30°
∵AD=BD,∠ADB=∠ADC,DE=DC
∴△BDE≌△ADC(SAS)
∴∠DAC=∠DBE=30°
故选:C.
7.【解答】解:①∵D是BC的中点,AB=AC,
∴AD⊥BC,故①正确;
②∵F在AE上,不一定是AE的中点,AC=CE,
∴无法证明CF⊥AE,故②错误;
③无法证明∠1=∠2,故③错误;
④∵D是BC的中点,
∴BD=DC,
∵AB=CE,
∴AB+BD=CE+DC=DE,故④正确.
故其中正确的结论有①④,共两个.
故选:B.
8.【解答】解:∵AE⊥CE于点E,BD⊥CD于点D,
∴∠AEC=∠D=90°,
在Rt△AEC与Rt△CDB中,
∴Rt△AEC≌Rt△CDB(HL),
∴CE=BD=2,CD=AE=7,
∴DE=CD﹣CE=7﹣2=5,
故选:B.
9.【解答】解:在△ABC和△DEC中,,
△ABC≌△DEC(SAS),
∴AB=DE=58米,
故选:A.
10.【解答】解:∵滑梯、墙、地面正好构成直角三角形,
∵BC=EF,AC=DF,
∴Rt△ABC≌Rt△DEF(HL),
∴∠1=∠4,
∵∠3+∠4=90°,
∴∠ACB+∠DEF=90°.
故选:C.
二.填空题
11.【解答】解:∵AB∥CD,
∴∠B=∠DCE,
∵C是BE的中点,
∴BC=CE,
∴当添加BA=CD时,可根据“SAS”判断△ABC≌△DCE;
当添加∠A=∠D时,可根据“AAS”判断△ABC≌△DCE;
当添加AC∥DE或∠ACB=∠DEC时,可根据“SAS”判断△ABC≌△DCE.
故答案为BA=CD或∠A=∠D或AC∥DE或∠ACB=∠DEC.
12.【解答】解:∵AB⊥CF,AB∥DE,
∴△ABC和△DEF都是直角三角形.
∵CE=FB,CE为公共部分,
∴CB=EF,
又∵AB=DE,
∴△ABC≌△DEF(SAS).
故答案为:SAS.
13.【解答】解:在Rt△ABC与Rt△DEF中,
∵∠B=∠E=90°,AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(HL)
∴∠D=∠A=50°,
∴∠DFE=90°﹣∠D=90°﹣50°=40°.
故填40.
14.【解答】解:①直角三角形两直角对应相等,有一边对应相等的两个直角三角形只具备一边与一角对应相等,所以有一边对应相等的两个直角三角形不一定全等;
②直角三角形是特殊的三角形,所以一般三角形具有的性质,直角三角形都具有;
③如果一个直角三角形的两直角边与另一个直角三角形的一条直角边与斜边分别相等,那么这两个直角三角形不全等,所以有两边相等的两直角三角形不一定全等;
④两直角三角形的斜边为5cm,一条直角边都为3cm,根据HL可得这两个直角三角形必全等.
所以正确的结论是②④.
故答案为2.
15.【解答】解:在△DCE和△ABD中,
∵,
∴△DCE≌△ABD(SAS),
∴∠CDE=∠DAB,
∵∠CDE+∠ADC=∠ADC+∠DAB=90°,
∴∠AFD=90°,
∴∠BAC+∠ACD=90°,
故答案为:90.
16.【解答】解:连接AB,如图,
在△OAB和△OA′B′中,
∴△OAB≌△OA′B′(SAS),
∴A′B′=AB=5(m).
答:槽宽为5m.
故答案为:5.
17.【解答】解:根据题意可知∠B=∠D=90°,BC=CD,∠ACB=∠ECD
∴△ABC≌△EDC(ASA)
∴AB=DE=50米.
故答案为:50
18.【解答】解:∵四边形ABCD是正方形
∴AD=AB,∠B=∠BAD=90°
∵AQ⊥DP
∴∠QAD+∠ADP=90°,且∠DAQ+∠BAQ=90°
∴∠BAQ=∠ADP,且∠B=∠BAD=90°,AD=AB
∴△ABQ≌△DAP(ASA)
∴AP=CQ
∴2t=8﹣t
∴t=
故答案为:
三.解答题
19.【解答】证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(AAS).
20.【解答】解:添加AB=AE,
理由如下:∵AB=AE,∠A=∠A,AC=AD
∴△ABC≌△AED(SAS)
21.【解答】证明:在Rt△ABE和Rt△CBF中,
∵,
∴Rt△ABE≌Rt△CBF(HL).
22.【解答】证明:∵BF=EC,
∴BF+FC=FC+EC,即BC=EF,
∵∠A=∠D=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL).
23.【解答】解:AG=DH;理由如下:
∵AB∥CD、EC∥BF,
∴四边形BFCE是平行四边形,∠A=∠D,
∴∠BEC=∠BFC,BE=CF,
∴∠AEG=∠DFH,
∵AB=CD,
∴AE=DF,
在△AEG和△DFH中,,
∴△AEG≌△DFH(ASA),
∴AG=DH.
24.【解答】(1)证明:∵∠ACB=∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,,
∴△ACD≌△BCE(SAS);
(2)解:由(1)知:△ACD≌△BCE,
∴AD=BE=5,
∴AB=AD+BD=5+2=7.
25.【解答】(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中
,
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=10m,BF=3m,
∴FC=10﹣3﹣3=4m.
一.选择题(共10小题,每小题3分,共30分)
1.如图,DE⊥AC,BF⊥AC,垂足分别是E,F,且DE=BF,若利用“HL”证明△DEC≌△BFA,则需添加的条件是( )
A.EC=FA B.DC=BA C.∠D=∠B D.∠DCE=∠BAF
2.如图,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠CAP=∠APQ,PR=PS.下列结论:其中结论正确的序号是( )
①AS=AR;
②QP∥AR;
③△BRP≌△CSP
A.①② B.②③ C.①③ D.①②③
3.如图,点E,点F在直线AC上,DF=BE,∠AFD=∠CEB,下列条件中不能判断△ADF≌△CBE的是( )
A.∠B=∠D B.AD=CB C.AE=CF D.∠A=∠C
4.下列说法:①一个底角和一条边分别相等的两个等腰三角形全等;②底边及底边上的高分别相等的两个等腰三角形全等;③两边分别相等的两个直角三角形全等;④一个锐角和一条边分别相等的两个直角三角形全等,其中正确的个数是( )
A.1 B.2 C.3 D.4
5.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是( )
A.HL B.SAS C.ASA D.AAS
6.如图,AD是△ABC的高,AD=BD,DE=DC,∠BAC=75°,则∠DBE的度数是( )
A.10° B.15° C.30° D.45°
7.如图,点C是△ABE的BE边上一点,点F在AE上,D是BC的中点,且AB=AC=
CE,给出下列结论:①AD⊥BC;②CF⊥AE;③∠1=∠2;④AB+BD=DE.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
8.如图,AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,AE=7,BD=2,则DE的长是( )
A.7 B.5 C.3 D.2
9.如图,有一池塘,要测池塘两端A,B间的距离,可先在平地上取一个不经过池塘可以直接到达点A和B的点C,连接AC并延长至D,使CD=CA,连接BC并延长至E,使CE=CB,连接ED.若量出DE=58米,则A,B间的距离即可求.依据是( )
A.SAS B.SSS C.AAS D.ASA
10.如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
二.填空题(共8小题,每小题3分,共24分)
11.如图,AB∥CD,C是BE的中点,要想使得△ABC≌△DCE,还需要添加的条件是 (添加一个即可)
12.如图,AB⊥CF,垂足为B,AB∥DE,点E在CF上,CE=FB,AB=DE,依据以上条件可以判定△ABC≌△DEF,这种判定三角形全等的方法,可以简写为 .
13.如图,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,∠A=50°,则∠DFE= .
14.下列语句:①有一边对应相等的两个直角三角形全等;②一般三角形具有的性质,直角三角形都具有;③有两边相等的两直角三角形全等;④两直角三角形的斜边为5cm,一条直角边都为3cm,则这两个直角三角形必全等.其中正确的有 个.
15.如图所示的网格是正方形网格,点A,B,C,D均落在格点上,则∠BAC+∠ACD= °.
16.如图,是一个测量工件内槽宽的工具,点O既是AA'的中点,也是BB'的中点,若测得AB=5cm,则该内槽A'B'的宽为 cm.
17.如图,要在湖两岸A,B两点之间修建一座观赏桥,由于条件限制,无法直接测量A、B两点间的距离,于是小明想出来这样一种做法:在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使A,C,E三点在一条直线上,这时测得DE=50米,则AB= 米.
18.如图,在正方形ABCD中,AB=8厘米,如果动点P在线段AB上以2厘米/秒的速度由A点向B点运动,同时动点Q在以1厘米/秒的速度线段BC上由C点向B点运动,当点P到达B点时整个运动过程停止.设运动时间为t秒,当AQ⊥DP时,t的值为 秒.
三.解答题(共7小题,共66分)
19.已知:如图,BE=FC,∠A=∠D,∠B=∠F.求证:△ABC≌△DFE.
20.如图,点D、C分别在线段AB、AE上,ED与BC相交于点O,已知AD=AC,请添加一个条件(不添加辅助线)使△ABC≌△AED,并说明理由
21.如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
求证:Rt△ABE≌Rt△CBF.
22.如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.
23.如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G、H,若AB=CD,探究AG与DH有怎样的数量关系.
24.如图,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,∠ACB=∠DCE,点D在线段AB上(与A,B不重合),连接BE.
(1)证明:△ACD≌△BCE.
(2)若BD=2,BE=5,求AB的长.
25.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,AB∥DE,∠A=∠D,测得AB=DE.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
参考答案
一.选择题
1.【解答】解:∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°,
∵DE=BF,
∴当添加条件DC=BA时,可利用“HL”证明△DEC≌△BFA.
故选:B.
2.【解答】解:∵PR⊥AB,PS⊥AC,
∴∠PRA=∠PSA=90°,
∵AP=AP,PR=PS,
∴Rt△APR≌Rt△APS(HL),
∴AR=AS,所以①正确;
∠PAR=∠PAS,
∵∠CAP=∠APQ,
∴∠PAR=∠APQ,
∴QP∥AR,所以②正确;
在△BRP和△CSP中,因为只有∠PRB=∠PSC=90°,PR=PS,所以不能判断这两和三角形全等,所以③错误.
故选:A.
3.【解答】解:A、添加∠B=∠D,由全等三角形的判定定理ASA可以判定△ADF≌△CBE,故本选项错误.
B、添加AD=CB,由全等三角形的判定定理SSA不能判定△ADF≌△CBE,故本选项正确.
C、添加AE=CF,可以得到AF=CE,由全等三角形的判定定理SAS可以判定△ADF≌△CBE,故本选项错误.
D、添加∠A=∠C,由全等三角形的判定定理AAS可以判定△ADF≌△CBE,故本选项错误.
故选:B.
4.【解答】解:①一个底角和一条边分别相等的两个等腰三角形不一定全等;
②底边及底边上的高分别相等的两个等腰三角形全等,正确;
③两边分别相等的两个直角三角形不一定全等;
④如果在两个直角三角形中,例如:两个30°角的直角三角形,一个三角形的直角边与另一个三角形的斜边相等,这两个直角三角形肯定不全等,错误;
故选:A.
5.【解答】解:在Rt△AOB和Rt△COD中,
,
∴Rt△AOB≌Rt△COD(HL),
则如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是HL,
故选:A.
6.【解答】证明:∵AD=BD,AD⊥BC
∴∠BAD=∠ABD=45°
∵∠DAC=∠BAC﹣∠BAD
∴∠DAC=75°﹣45°=30°
∵AD=BD,∠ADB=∠ADC,DE=DC
∴△BDE≌△ADC(SAS)
∴∠DAC=∠DBE=30°
故选:C.
7.【解答】解:①∵D是BC的中点,AB=AC,
∴AD⊥BC,故①正确;
②∵F在AE上,不一定是AE的中点,AC=CE,
∴无法证明CF⊥AE,故②错误;
③无法证明∠1=∠2,故③错误;
④∵D是BC的中点,
∴BD=DC,
∵AB=CE,
∴AB+BD=CE+DC=DE,故④正确.
故其中正确的结论有①④,共两个.
故选:B.
8.【解答】解:∵AE⊥CE于点E,BD⊥CD于点D,
∴∠AEC=∠D=90°,
在Rt△AEC与Rt△CDB中,
∴Rt△AEC≌Rt△CDB(HL),
∴CE=BD=2,CD=AE=7,
∴DE=CD﹣CE=7﹣2=5,
故选:B.
9.【解答】解:在△ABC和△DEC中,,
△ABC≌△DEC(SAS),
∴AB=DE=58米,
故选:A.
10.【解答】解:∵滑梯、墙、地面正好构成直角三角形,
∵BC=EF,AC=DF,
∴Rt△ABC≌Rt△DEF(HL),
∴∠1=∠4,
∵∠3+∠4=90°,
∴∠ACB+∠DEF=90°.
故选:C.
二.填空题
11.【解答】解:∵AB∥CD,
∴∠B=∠DCE,
∵C是BE的中点,
∴BC=CE,
∴当添加BA=CD时,可根据“SAS”判断△ABC≌△DCE;
当添加∠A=∠D时,可根据“AAS”判断△ABC≌△DCE;
当添加AC∥DE或∠ACB=∠DEC时,可根据“SAS”判断△ABC≌△DCE.
故答案为BA=CD或∠A=∠D或AC∥DE或∠ACB=∠DEC.
12.【解答】解:∵AB⊥CF,AB∥DE,
∴△ABC和△DEF都是直角三角形.
∵CE=FB,CE为公共部分,
∴CB=EF,
又∵AB=DE,
∴△ABC≌△DEF(SAS).
故答案为:SAS.
13.【解答】解:在Rt△ABC与Rt△DEF中,
∵∠B=∠E=90°,AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(HL)
∴∠D=∠A=50°,
∴∠DFE=90°﹣∠D=90°﹣50°=40°.
故填40.
14.【解答】解:①直角三角形两直角对应相等,有一边对应相等的两个直角三角形只具备一边与一角对应相等,所以有一边对应相等的两个直角三角形不一定全等;
②直角三角形是特殊的三角形,所以一般三角形具有的性质,直角三角形都具有;
③如果一个直角三角形的两直角边与另一个直角三角形的一条直角边与斜边分别相等,那么这两个直角三角形不全等,所以有两边相等的两直角三角形不一定全等;
④两直角三角形的斜边为5cm,一条直角边都为3cm,根据HL可得这两个直角三角形必全等.
所以正确的结论是②④.
故答案为2.
15.【解答】解:在△DCE和△ABD中,
∵,
∴△DCE≌△ABD(SAS),
∴∠CDE=∠DAB,
∵∠CDE+∠ADC=∠ADC+∠DAB=90°,
∴∠AFD=90°,
∴∠BAC+∠ACD=90°,
故答案为:90.
16.【解答】解:连接AB,如图,
在△OAB和△OA′B′中,
∴△OAB≌△OA′B′(SAS),
∴A′B′=AB=5(m).
答:槽宽为5m.
故答案为:5.
17.【解答】解:根据题意可知∠B=∠D=90°,BC=CD,∠ACB=∠ECD
∴△ABC≌△EDC(ASA)
∴AB=DE=50米.
故答案为:50
18.【解答】解:∵四边形ABCD是正方形
∴AD=AB,∠B=∠BAD=90°
∵AQ⊥DP
∴∠QAD+∠ADP=90°,且∠DAQ+∠BAQ=90°
∴∠BAQ=∠ADP,且∠B=∠BAD=90°,AD=AB
∴△ABQ≌△DAP(ASA)
∴AP=CQ
∴2t=8﹣t
∴t=
故答案为:
三.解答题
19.【解答】证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(AAS).
20.【解答】解:添加AB=AE,
理由如下:∵AB=AE,∠A=∠A,AC=AD
∴△ABC≌△AED(SAS)
21.【解答】证明:在Rt△ABE和Rt△CBF中,
∵,
∴Rt△ABE≌Rt△CBF(HL).
22.【解答】证明:∵BF=EC,
∴BF+FC=FC+EC,即BC=EF,
∵∠A=∠D=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL).
23.【解答】解:AG=DH;理由如下:
∵AB∥CD、EC∥BF,
∴四边形BFCE是平行四边形,∠A=∠D,
∴∠BEC=∠BFC,BE=CF,
∴∠AEG=∠DFH,
∵AB=CD,
∴AE=DF,
在△AEG和△DFH中,,
∴△AEG≌△DFH(ASA),
∴AG=DH.
24.【解答】(1)证明:∵∠ACB=∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,,
∴△ACD≌△BCE(SAS);
(2)解:由(1)知:△ACD≌△BCE,
∴AD=BE=5,
∴AB=AD+BD=5+2=7.
25.【解答】(1)证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中
,
∴△ABC≌△DEF;
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BF+FC=EC+FC,
∴BF=EC,
∵BE=10m,BF=3m,
∴FC=10﹣3﹣3=4m.
