人教版 信息技术 必修1 左偏堆的特点及其应用课件(共21张ppt)
文档属性
| 名称 | 人教版 信息技术 必修1 左偏堆的特点及其应用课件(共21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 257.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2019-08-22 00:00:00 | ||
图片预览





文档简介
课件21张PPT。左偏树的特点及其应用1左偏树的定义左偏树(Leftist Tree)是一种可并堆(Mergeable Heap) ,它除了支持优先队列的三个基本操作(插入,删除,取最小节点),还支持一个很特殊的操作——合并操作。
左偏树是一棵堆有序(Heap Ordered)二叉树。
左偏树满足左偏性质(Leftist Property)。1左偏树的定义 —— 左偏性质定义一棵左偏树中的外节点(External Node) 为左子树或右子树为空的节点。
定义节点 i 的距离(dist(i)) 为节点 i 到它的后代中,最近的外节点所经过的边数。
任意节点的左子节点的距离不小于右子节点的距离(左偏性质)。
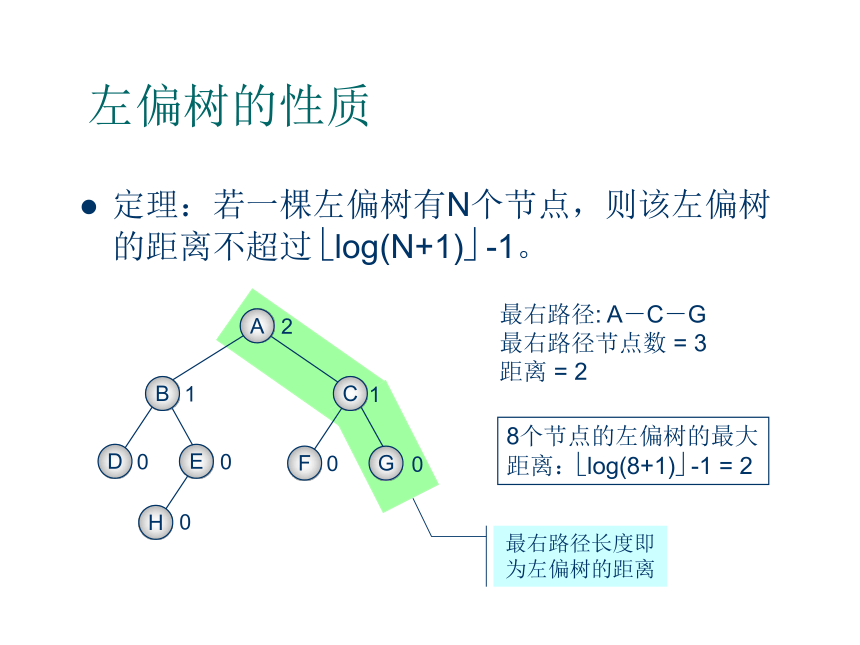
由左偏性质可知,一个节点的距离等于以该节点为根的子树最右路径的长度。1左偏树的性质定理:若一棵左偏树有N个节点,则该左偏树的距离不超过 ?log(N+1)? -1。最右路径: A-C-G
最右路径节点数 = 3
距离 = 28个节点的左偏树的最大距离:?log(8+1)? -1 = 21左偏树的操作左偏树支持下面这些操作:
MakeNull —— 初始化一棵空的左偏树
Merge —— 合并两棵左偏树
Insert —— 插入一个新节点
Min —— 取得最小节点
DeleteMin —— 删除最小节点
Delete —— 删除任意已知节点
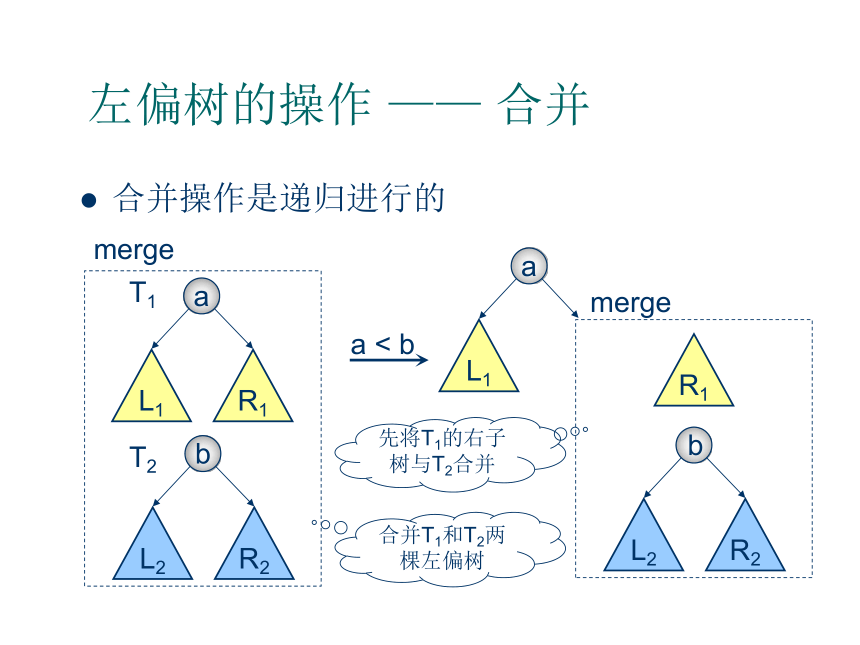
Decrease —— 减小一个节点的键值1左偏树的操作 —— 合并合并操作是递归进行的
合并T1和T2两棵左偏树先将T1的右子树与T2合并1左偏树的操作 —— 合并合并操作是递归进行的
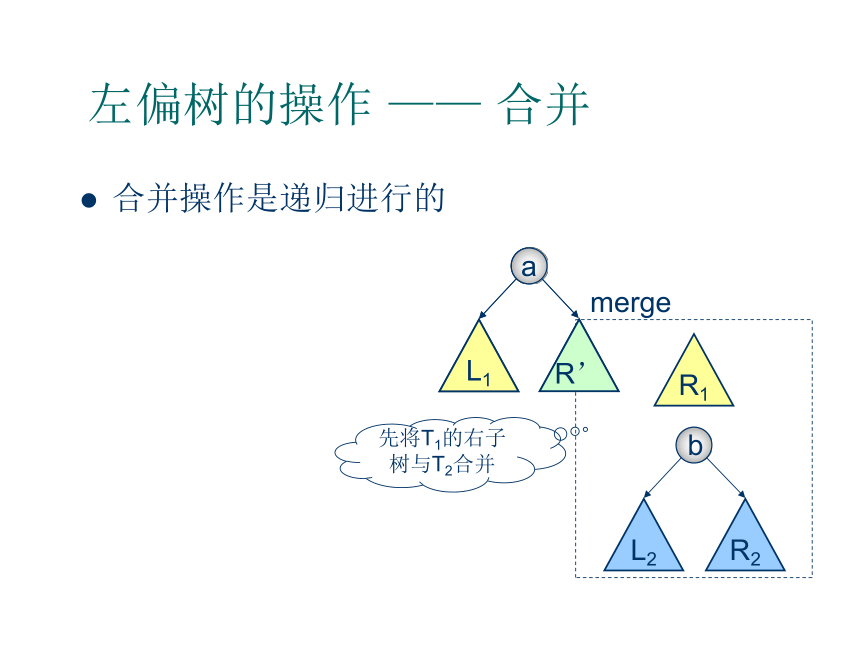
aL1R’先将T1的右子树与T2合并1左偏树的操作 —— 合并合并操作是递归进行的
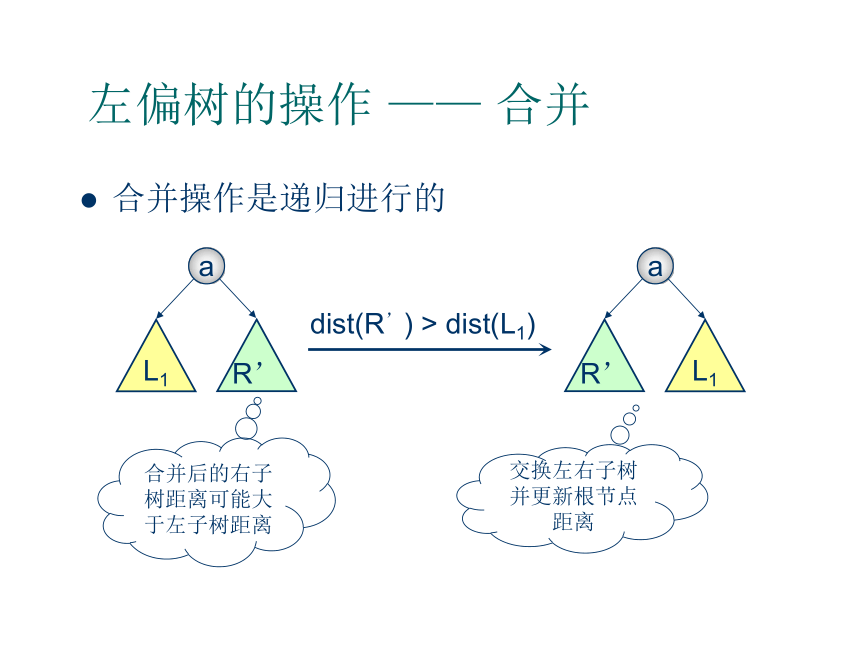
交换左右子树并更新根节点距离合并后的右子树距离可能大于左子树距离1左偏树的操作 —— 合并合并操作的代码如下:
Function Merge(A, B)
If A = NULL Then return B
If B = NULL Then return A
If key(B) < key(A) Then swap(A, B)
right(A) ← Merge(right(A), B)
If dist(right(A)) > dist(left(A)) Then
swap(left(A), right(A))
If right(A) = NULL Then dist(A) ← 0
Else dist(A) ← dist(right(A)) + 1
return A
End Function1左偏树的操作 —— 合并下面是一个合并的例子:
1左偏树的操作 —— 合并下面是一个合并的例子:
1左偏树的操作 —— 合并下面是一个合并的例子:
1左偏树的操作 —— 合并下面是一个合并的例子:
18NULL1左偏树的操作 —— 合并下面是一个合并的例子:
37701?1左偏树的操作 —— 合并下面是一个合并的例子:
11226173718871左偏树的操作 —— 合并下面是一个合并的例子:
02?1左偏树的操作 —— 合并下面是一个合并的例子:
3102011左偏树的操作 —— 合并合并操作都是一直沿着两棵左偏树的最右路径进行的。
一棵N个节点的左偏树,最右路径上最多有 ?log(N+1)? 个节点。
因此,合并操作的时间复杂度为: O(log N1 + log N2) = O(log N)1左偏树的操作 —— 插入插入一个新节点
把待插入节点作为一棵单节点左偏树
合并两棵左偏树
时间复杂度:O(log N)1左偏树的操作 —— 删除删除最小节点
删除根节点
合并左右子树
时间复杂度:O(log N)1总结左偏树的特点:
时空效率高
编程复杂度低
左偏树的应用:
可并堆
优先队列性价比高补充二叉堆的不足
左偏树是一棵堆有序(Heap Ordered)二叉树。
左偏树满足左偏性质(Leftist Property)。1左偏树的定义 —— 左偏性质定义一棵左偏树中的外节点(External Node) 为左子树或右子树为空的节点。
定义节点 i 的距离(dist(i)) 为节点 i 到它的后代中,最近的外节点所经过的边数。
任意节点的左子节点的距离不小于右子节点的距离(左偏性质)。
由左偏性质可知,一个节点的距离等于以该节点为根的子树最右路径的长度。1左偏树的性质定理:若一棵左偏树有N个节点,则该左偏树的距离不超过 ?log(N+1)? -1。最右路径: A-C-G
最右路径节点数 = 3
距离 = 28个节点的左偏树的最大距离:?log(8+1)? -1 = 21左偏树的操作左偏树支持下面这些操作:
MakeNull —— 初始化一棵空的左偏树
Merge —— 合并两棵左偏树
Insert —— 插入一个新节点
Min —— 取得最小节点
DeleteMin —— 删除最小节点
Delete —— 删除任意已知节点
Decrease —— 减小一个节点的键值1左偏树的操作 —— 合并合并操作是递归进行的
合并T1和T2两棵左偏树先将T1的右子树与T2合并1左偏树的操作 —— 合并合并操作是递归进行的
aL1R’先将T1的右子树与T2合并1左偏树的操作 —— 合并合并操作是递归进行的
交换左右子树并更新根节点距离合并后的右子树距离可能大于左子树距离1左偏树的操作 —— 合并合并操作的代码如下:
Function Merge(A, B)
If A = NULL Then return B
If B = NULL Then return A
If key(B) < key(A) Then swap(A, B)
right(A) ← Merge(right(A), B)
If dist(right(A)) > dist(left(A)) Then
swap(left(A), right(A))
If right(A) = NULL Then dist(A) ← 0
Else dist(A) ← dist(right(A)) + 1
return A
End Function1左偏树的操作 —— 合并下面是一个合并的例子:
1左偏树的操作 —— 合并下面是一个合并的例子:
1左偏树的操作 —— 合并下面是一个合并的例子:
1左偏树的操作 —— 合并下面是一个合并的例子:
18NULL1左偏树的操作 —— 合并下面是一个合并的例子:
37701?1左偏树的操作 —— 合并下面是一个合并的例子:
11226173718871左偏树的操作 —— 合并下面是一个合并的例子:
02?1左偏树的操作 —— 合并下面是一个合并的例子:
3102011左偏树的操作 —— 合并合并操作都是一直沿着两棵左偏树的最右路径进行的。
一棵N个节点的左偏树,最右路径上最多有 ?log(N+1)? 个节点。
因此,合并操作的时间复杂度为: O(log N1 + log N2) = O(log N)1左偏树的操作 —— 插入插入一个新节点
把待插入节点作为一棵单节点左偏树
合并两棵左偏树
时间复杂度:O(log N)1左偏树的操作 —— 删除删除最小节点
删除根节点
合并左右子树
时间复杂度:O(log N)1总结左偏树的特点:
时空效率高
编程复杂度低
左偏树的应用:
可并堆
优先队列性价比高补充二叉堆的不足
同课章节目录
