北师大版七年级数学上册第四章基本平面图形单元测试题解析版
文档属性
| 名称 | 北师大版七年级数学上册第四章基本平面图形单元测试题解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 279.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 10:22:49 | ||
图片预览



文档简介
北师大版七年级数学上册 第四章 基本平面图形 单元测试题
时间:100分钟 满分:120分
一、选择题(共10小题,每小题3分,共30分)
1.乘火车从北京到上海,共有25个车站(包括北京和上海在内),那么共需要准备多少种不同的车票( )
A. 400 B. 25 C. 600 D. 100
2.如图所示四幅图中,符合“射线PA与射线PB是同一条射线”的图为( )
A. B. C. D.
3.在墙壁上固定一根横放的木条,则至少需要钉子的枚数是( )
A. 1枚 B. 2枚 C. 3枚 D. 任意枚
4.如图,下列不正确的几何语句是( )
A. 直线AB与直线BA是同一条直线 B. 射线OA与射线OB是同一条射线
C. 射线OA与射线AB是同一条射线 D. 线段AB与线段BA是同一条线段
5.已知线段AB,延长AB至C,使AC=2BC,反向延长AB至D,使AD=BC,那么线段AD是线段AC的( )
A. B. C. D.
6.如图,AB=8cm,AD=BC=5cm,则CD等于( )
A. 1cm B. 2cm C. 3cm D. 4cm
7.下列说法中,正确的有( )个
①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若AB=BC,则点B是线段AC的中点;⑤射线AB和射线BA是同一条射线 ⑥直线有无数个端点.
A. 2个 B. 3个 C. 4个 D. 5个
8.如图,从点O出发的五条射线,可以组成( )个角.
A. 4 B. 6 C. 8 D. 10
9.时钟显示为8:30时,时针与分针所夹的角是( )
A. 90° B. 120° C. 75° D. 84°
10.如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于( )
A. 65° B. 50° C. 40° D. 25°
二、填空题(共8小题,每小题3分,共24分)
11.下列说法中正确的有(把正确的序号填到横线上).
①延长直线AB到C;②延长射线OA到C;③延长线段OA到C;④经过两点有且只有一条线段;⑤射线是直线的一半.
12.公园里准备修四条直的走廊,并且在走廊的每个交叉路口处设一个报亭,这样的报亭最多有____________个.
13.一点将一长为28cm的线段分成5:2的两段,该分点与原线段中点间的距离为cm.
14.数轴上A、B两点离开原点的距离分别为2和3,则AB两点间的距离为.
15.钟表上4时15分钟,时针与分针的夹角的度数是.
16.计算33°52′+21°54′=.
17.如图,点A、O、B在一条直线上,∠AOC=140°,OD是∠BOC的平分线,则∠COD=度.
18.如图,将三角形ABC纸片沿MN折叠,使点A落在点A′处,若∠A′MB=55°,则∠AMN=°.
三、解答题(共7小题,每小题8分,共56分)
19.已知平面上四点A、B、C、D,如图:
(1)画直线AD;
(2)画射线BC,与AD相交于O;
(3)连结AC、BD相交于点F.
20.如图,M是线段AB的中点,点C在线段AB上,且AC=8cm,N是AC的中点,MN=6cm,求线段AB的长.
21.如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=114°.求∠COD的度数.
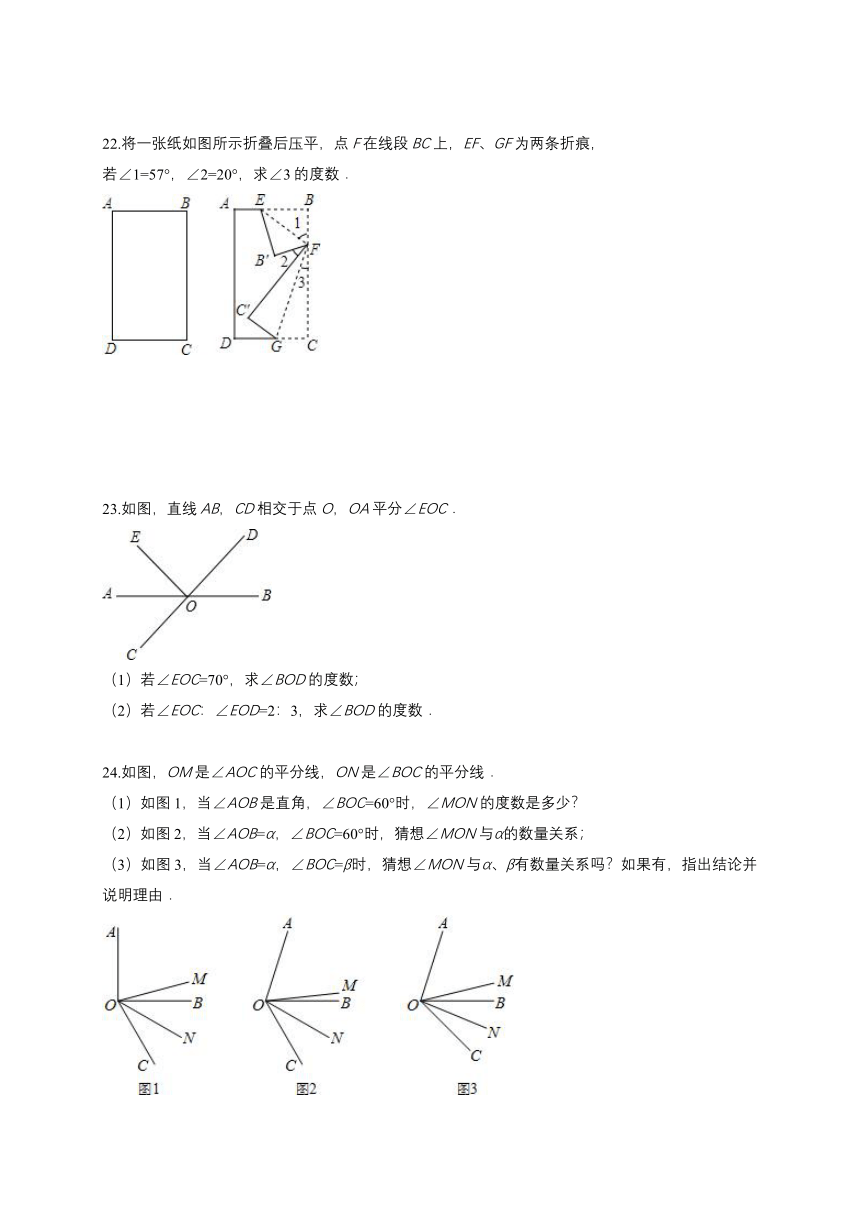
22.将一张纸如图所示折叠后压平,点F在线段BC上,EF、GF为两条折痕,
若∠1=57°,∠2=20°,求∠3的度数.
23.如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
24.如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
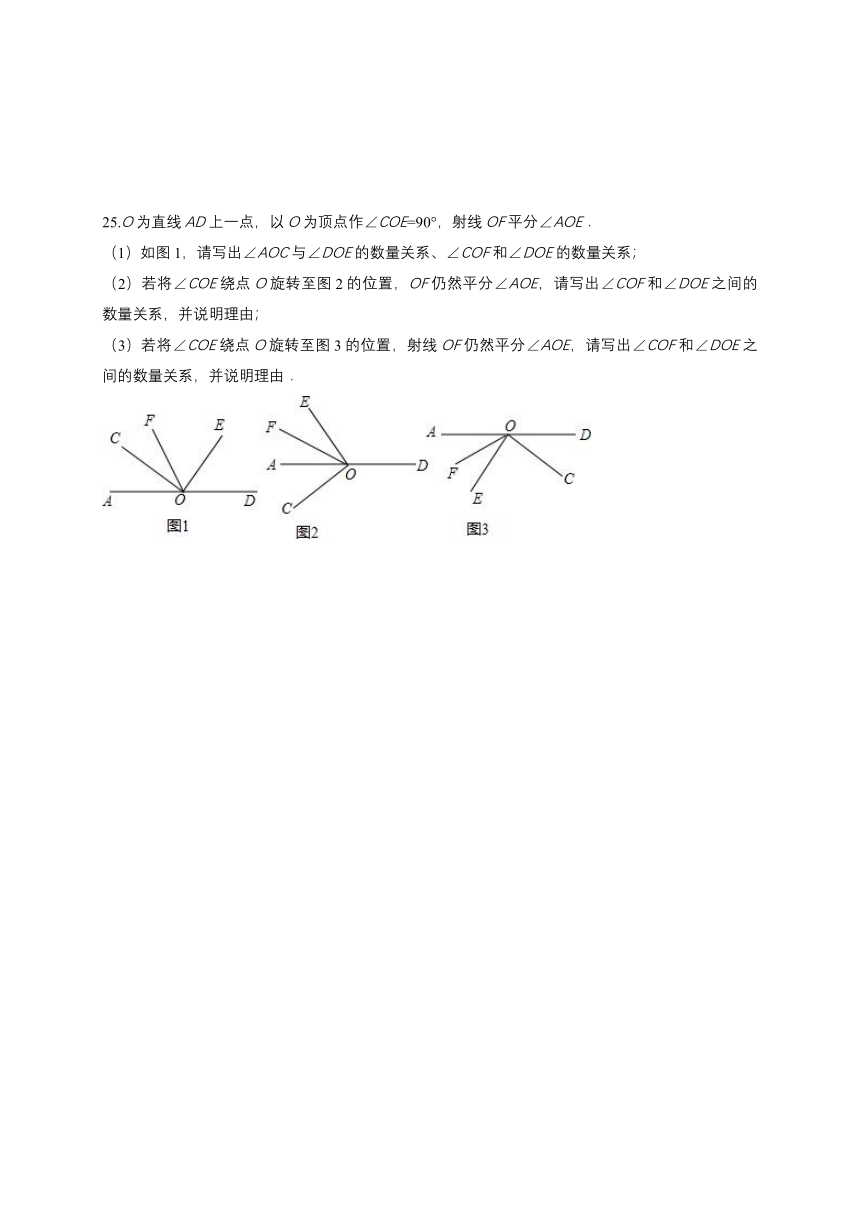
25.O为直线AD上一点,以O为顶点作∠COE=90°,射线OF平分∠AOE.
(1)如图1,请写出∠AOC与∠DOE的数量关系、∠COF和∠DOE的数量关系;
(2)若将∠COE绕点O旋转至图2的位置,OF仍然平分∠AOE,请写出∠COF和∠DOE之间的数量关系,并说明理由;
(3)若将∠COE绕点O旋转至图3的位置,射线OF仍然平分∠AOE,请写出∠COF和∠DOE之间的数量关系,并说明理由.
答案解析
1.【答案】C
【解析】∵共有25个车站,∴线段的条数为25(25-1)=600,
∴共需要准备600种不同的车票.故选C.
2.【答案】C
【解析】A.射线PA和射线PB不是同一条射线,故此选项错误;
B.射线PA和射线PB不是同一条射线,故此选项错误;
C.射线PA和射线PB是同一条射线,故此选项正确;
D.射线PA和射线PB不是同一条射线,故此选项错误;
故选C.
3.【答案】B
【解析】∵两点确定一条直线,∴至少需要2枚钉子.故选B.
4.【答案】C
【解析】A正确,因为直线向两方无限延伸;
B正确,射线的端点和方向都相同;
C错误,因为射线的端点不相同;
D正确.
故选C.
5.【答案】D
【解析】设BC=a,则AC=2a,AD=a,则,故选D.
6.【答案】B
【解析】∵AB=8cm,AD=5cm,∴BD=AB-AD=3cm,
∵BC=5cm,∴CD=CB-BD=2cm,故选B.
7.【答案】A
【解析】①过两点有且只有一条直线,正确,
②连接两点的线段叫做两点间的距离,不正确,应为连接两点的线段的长度叫做两点间的距离,
③两点之间,线段最短,正确,
④若AB=BC,则点B是线段AC的中点,不正确,只有点B在AC上时才成立,
⑤射线AB和射线BA是同一条射线,不正确,端点不同,
⑥直线有无数个端点.不正确,直线无端点.共2个正确,故选A.
8.【答案】D
【解析】点O出发的五条射线,可以组成的角有:∠AOB,∠AOC,∠AOD,∠AOE,∠BOC,∠BOD,∠BOE,∠COD,∠COE,∠DOE.故选D.
9.【答案】C
【解析】由于钟面被分成12大格,每格为30°,8点30分时,
钟面上时针指向数字8与9的中间,分针指向数字6,
所以时针与分针所成的角等于2×30°+×30°=75°.故选C.
10.【答案】A
【解析】∵∠AOB是一直角,∠AOC=40°,∴∠COB=50°,
∵OD平分∠BOC,∴∠COD=25°,
∵∠AOD=∠AOC+∠COD,∴∠AOD=65°.故选A.
11.【答案】③
【解析】①延长直线AB到C,说法错误;
②延长射线OA到C,说法错误;
③延长线段OA到C,说法正确;
④经过两点有且只有一条线段,说法错误;
⑤射线是直线的一半,说法错误;
故答案为:③.
12.【答案】6
【解析】∵有4条直线,最多与前4-1=3条直线有4-1=3个交点,
∴最多有4×(4-1)÷2=6个交点.故这样的报亭最多有6个.故答案为:6.
13.【答案】6
【解析】如图,AB=28cm,AC:BC=5:2,点D为AB的中点,
设AC=5x,则BC=2x,∵AC+BC=AB,∴5x+2x=28,解得x=4,∴AC=5x=20,
∵点D为AB的中点,∴AD=AB=14,∴CD=AC-AD=20-14=6(cm),
即该分点与原线段中点间的距离为6cm.故答案为6.
14.【答案】5或1
【解析】∵数轴上A、B两点离开原点的距离分别为2和3可得出点A表示±2,点B表示±3,
∴当点A、B在原点的同侧时,AB=|3-2|=1;
当点A、B在原点的异侧时,AB=|-2-3|=5.
故答案为:5或1.
15.【答案】()°
【解析】4时15分,时针与分针相距1+=份,
4时15分钟,时针与分针的夹角的度数30×=()°,
故答案为:()°.
16.【答案】55°46′
【解析】相同单位相加,满60,向前进1即可.33°52′+21°54′=54°106′=55°46′.
17.【答案】20
【解析】∵∠AOC与∠BOC是邻补角,∴∠AOC+∠BOC=180°,
∵∠AOC=140°,∴∠BOC=180°-140°=40°,
∵OD平分∠BOC,∴∠COD=∠COB=20°.故答案为:20.
18.【答案】62.5
【解析】∵∠A′MB=55°,∴∠AMA′=180°-∠A′MB=180°-55°=125°,
由折叠的性质得,∠A′MN=∠AMN=∠AMA′=×125°=62.5°,故答案为:62.5.
19.【答案】解:如图所示:
【解析】(1)画直线AD,连接AD并向两方无限延长;
(2)画射线BC,以B为端点向BC方向延长交AD于点O;
(3)连接各点,其交点即为点F.
20.【答案】解:由AC=8cm,N是AC的中点,得AN=AC=4cm.
由线段的和差,得AM=AN+MN=4+6=10cm.
由M是线段AB的中点,得AB=2AM=20cm,
线段AB的长是20cm.
【解析】根据线段中点的性质,可得AN的长,根据线段的和差,可得AM的长,根据线段中点的性质,可得答案.
21.【答案】解:∵OD平分∠AOB,∠AOB=114°,∴∠AOD=∠BOD=∠AOB=57°.
∵∠BOC=2∠AOC,∠AOB=114°,∴∠AOC=∠AOB=38°.
∴∠COD=∠AOD-∠AOC=57°-38°=19°.
【解析】根据OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=114°,可以求得∠AOC、∠AOD的度数,从而可以求得∠COD的度数.
22.【答案】解:如图由折叠可知,∠EFB′=∠1=57°,∠2=20°,∠3=∠GFC′,
∵∠EFB′+∠1+∠2+∠3+∠GFC′=180°,∴∠3==23°.
【解析】根据折叠的特点可找到相等的角,在展开图中,利用∠EFB′+∠1+∠2+∠3+∠GFC′等于平角得出结论.
23.【答案】解:(1)∵OA平分∠EOC,∴∠AOC=∠EOC=×70°=35°,∴∠BOD=∠AOC=35°;
(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,∴∠AOC=∠EOC=×72°=36°,∴∠BOD=∠AOC=36°.
【解析】(1)根据角平分线定义得到∠AOC=∠EOC=×70°=35°,然后根据对顶角相等得到∠BOD=∠AOC=35°;
(2)先设∠EOC=2x,∠EOD=3x,根据平角的定义得2x+3x=180°,解得x=36°,则∠EOC=2x=72°,然后与(1)的计算方法一样.
24.【答案】解:(1)如图1,∵∠AOB=90°,∠BOC=60°,∴∠AOC=90°+60°=150°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC=75°,∠NOC=∠BOC=30°,∴∠MON=∠MOC-∠NOC=45°.
(2)如图2,∠MON=α,
理由是:∵∠AOB=α,∠BOC=60°,∴∠AOC=α+60°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC=α+30°,∠NOC=∠BOC=30°
∴∠MON=∠MOC-∠NOC=(α+30°)-30°=α.
(3)如图3,∠MON=α,与β的大小无关.
理由:∵∠AOB=α,∠BOC=β,∴∠AOC=α+β.
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=∠AOC=(α+β),∠NOC=∠BOC=β,
∴∠AON=∠AOC-∠NOC=α+β-β=α+β.
∴∠MON=∠MOC-∠NOC=(α+β)-β=α,即∠MON=α.
【解析】(1)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可;
(2)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可;
(3)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可.
25.【答案】解:(1)∵∠COE=90°,∠COE+∠AOC+∠DOE=180°,∴∠AOC+∠DOE=90°,
∵射线OF平分∠AOE,∴∠AOF=∠EOF=∠AOE,
∴∠COF=∠AOF-∠AOC=∠AOE-(90°-∠DOE)=(180°?∠DOE)?90°+∠DOE=∠DOE,
即∠AOC+∠DOE=90°,∠COF=∠DOE.
(2)数量关系:∠COF=∠DOE.
∵OF平分∠AOE,∴∠AOF=∠AOE,
∵∠COE=90°,∴∠AOC=90°-∠AOE,
∴∠COF=∠AOC+∠AOF=90°-∠AOE+∠AOE=90°-∠AOE,
∵∠AOE=180°-∠DOE,
∴∠COF=90°-(180°-∠DOE)=∠DOE,即∠COF=∠DOE;
(3)数量关系:∠COF=180°?∠DOE.
∵OF平分∠AOE,∴∠EOF=∠AOE,
∴∠COF=∠COE+∠EOF=90°+∠AOE=90°+(180°?∠DOE)=180°-∠DOE,
即∠COF=180°?∠DOE
【解析】(1)根据已知条件和图形可知:∠COE=90°,∠COE+∠AOC+∠DOE=180°,从而可以得到∠AOC与∠DOE的数量关系;由射线OF平分∠AOE,∠AOC与∠DOE的数量关系,从而可以得到∠COF和∠DOE的数量关系;
(2)由图2,可以得到各个角之间的关系,从而可以得到∠COF和∠DOE之间的数量关系;
(3)由图3和已知条件可以建立各个角之间的关系,从而可以得到∠COF和∠DOE之间的数量关系.
时间:100分钟 满分:120分
一、选择题(共10小题,每小题3分,共30分)
1.乘火车从北京到上海,共有25个车站(包括北京和上海在内),那么共需要准备多少种不同的车票( )
A. 400 B. 25 C. 600 D. 100
2.如图所示四幅图中,符合“射线PA与射线PB是同一条射线”的图为( )
A. B. C. D.
3.在墙壁上固定一根横放的木条,则至少需要钉子的枚数是( )
A. 1枚 B. 2枚 C. 3枚 D. 任意枚
4.如图,下列不正确的几何语句是( )
A. 直线AB与直线BA是同一条直线 B. 射线OA与射线OB是同一条射线
C. 射线OA与射线AB是同一条射线 D. 线段AB与线段BA是同一条线段
5.已知线段AB,延长AB至C,使AC=2BC,反向延长AB至D,使AD=BC,那么线段AD是线段AC的( )
A. B. C. D.
6.如图,AB=8cm,AD=BC=5cm,则CD等于( )
A. 1cm B. 2cm C. 3cm D. 4cm
7.下列说法中,正确的有( )个
①过两点有且只有一条直线;②连接两点的线段叫做两点间的距离;③两点之间,线段最短;④若AB=BC,则点B是线段AC的中点;⑤射线AB和射线BA是同一条射线 ⑥直线有无数个端点.
A. 2个 B. 3个 C. 4个 D. 5个
8.如图,从点O出发的五条射线,可以组成( )个角.
A. 4 B. 6 C. 8 D. 10
9.时钟显示为8:30时,时针与分针所夹的角是( )
A. 90° B. 120° C. 75° D. 84°
10.如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于( )
A. 65° B. 50° C. 40° D. 25°
二、填空题(共8小题,每小题3分,共24分)
11.下列说法中正确的有(把正确的序号填到横线上).
①延长直线AB到C;②延长射线OA到C;③延长线段OA到C;④经过两点有且只有一条线段;⑤射线是直线的一半.
12.公园里准备修四条直的走廊,并且在走廊的每个交叉路口处设一个报亭,这样的报亭最多有____________个.
13.一点将一长为28cm的线段分成5:2的两段,该分点与原线段中点间的距离为cm.
14.数轴上A、B两点离开原点的距离分别为2和3,则AB两点间的距离为.
15.钟表上4时15分钟,时针与分针的夹角的度数是.
16.计算33°52′+21°54′=.
17.如图,点A、O、B在一条直线上,∠AOC=140°,OD是∠BOC的平分线,则∠COD=度.
18.如图,将三角形ABC纸片沿MN折叠,使点A落在点A′处,若∠A′MB=55°,则∠AMN=°.
三、解答题(共7小题,每小题8分,共56分)
19.已知平面上四点A、B、C、D,如图:
(1)画直线AD;
(2)画射线BC,与AD相交于O;
(3)连结AC、BD相交于点F.
20.如图,M是线段AB的中点,点C在线段AB上,且AC=8cm,N是AC的中点,MN=6cm,求线段AB的长.
21.如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=114°.求∠COD的度数.
22.将一张纸如图所示折叠后压平,点F在线段BC上,EF、GF为两条折痕,
若∠1=57°,∠2=20°,求∠3的度数.
23.如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
24.如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
25.O为直线AD上一点,以O为顶点作∠COE=90°,射线OF平分∠AOE.
(1)如图1,请写出∠AOC与∠DOE的数量关系、∠COF和∠DOE的数量关系;
(2)若将∠COE绕点O旋转至图2的位置,OF仍然平分∠AOE,请写出∠COF和∠DOE之间的数量关系,并说明理由;
(3)若将∠COE绕点O旋转至图3的位置,射线OF仍然平分∠AOE,请写出∠COF和∠DOE之间的数量关系,并说明理由.
答案解析
1.【答案】C
【解析】∵共有25个车站,∴线段的条数为25(25-1)=600,
∴共需要准备600种不同的车票.故选C.
2.【答案】C
【解析】A.射线PA和射线PB不是同一条射线,故此选项错误;
B.射线PA和射线PB不是同一条射线,故此选项错误;
C.射线PA和射线PB是同一条射线,故此选项正确;
D.射线PA和射线PB不是同一条射线,故此选项错误;
故选C.
3.【答案】B
【解析】∵两点确定一条直线,∴至少需要2枚钉子.故选B.
4.【答案】C
【解析】A正确,因为直线向两方无限延伸;
B正确,射线的端点和方向都相同;
C错误,因为射线的端点不相同;
D正确.
故选C.
5.【答案】D
【解析】设BC=a,则AC=2a,AD=a,则,故选D.
6.【答案】B
【解析】∵AB=8cm,AD=5cm,∴BD=AB-AD=3cm,
∵BC=5cm,∴CD=CB-BD=2cm,故选B.
7.【答案】A
【解析】①过两点有且只有一条直线,正确,
②连接两点的线段叫做两点间的距离,不正确,应为连接两点的线段的长度叫做两点间的距离,
③两点之间,线段最短,正确,
④若AB=BC,则点B是线段AC的中点,不正确,只有点B在AC上时才成立,
⑤射线AB和射线BA是同一条射线,不正确,端点不同,
⑥直线有无数个端点.不正确,直线无端点.共2个正确,故选A.
8.【答案】D
【解析】点O出发的五条射线,可以组成的角有:∠AOB,∠AOC,∠AOD,∠AOE,∠BOC,∠BOD,∠BOE,∠COD,∠COE,∠DOE.故选D.
9.【答案】C
【解析】由于钟面被分成12大格,每格为30°,8点30分时,
钟面上时针指向数字8与9的中间,分针指向数字6,
所以时针与分针所成的角等于2×30°+×30°=75°.故选C.
10.【答案】A
【解析】∵∠AOB是一直角,∠AOC=40°,∴∠COB=50°,
∵OD平分∠BOC,∴∠COD=25°,
∵∠AOD=∠AOC+∠COD,∴∠AOD=65°.故选A.
11.【答案】③
【解析】①延长直线AB到C,说法错误;
②延长射线OA到C,说法错误;
③延长线段OA到C,说法正确;
④经过两点有且只有一条线段,说法错误;
⑤射线是直线的一半,说法错误;
故答案为:③.
12.【答案】6
【解析】∵有4条直线,最多与前4-1=3条直线有4-1=3个交点,
∴最多有4×(4-1)÷2=6个交点.故这样的报亭最多有6个.故答案为:6.
13.【答案】6
【解析】如图,AB=28cm,AC:BC=5:2,点D为AB的中点,
设AC=5x,则BC=2x,∵AC+BC=AB,∴5x+2x=28,解得x=4,∴AC=5x=20,
∵点D为AB的中点,∴AD=AB=14,∴CD=AC-AD=20-14=6(cm),
即该分点与原线段中点间的距离为6cm.故答案为6.
14.【答案】5或1
【解析】∵数轴上A、B两点离开原点的距离分别为2和3可得出点A表示±2,点B表示±3,
∴当点A、B在原点的同侧时,AB=|3-2|=1;
当点A、B在原点的异侧时,AB=|-2-3|=5.
故答案为:5或1.
15.【答案】()°
【解析】4时15分,时针与分针相距1+=份,
4时15分钟,时针与分针的夹角的度数30×=()°,
故答案为:()°.
16.【答案】55°46′
【解析】相同单位相加,满60,向前进1即可.33°52′+21°54′=54°106′=55°46′.
17.【答案】20
【解析】∵∠AOC与∠BOC是邻补角,∴∠AOC+∠BOC=180°,
∵∠AOC=140°,∴∠BOC=180°-140°=40°,
∵OD平分∠BOC,∴∠COD=∠COB=20°.故答案为:20.
18.【答案】62.5
【解析】∵∠A′MB=55°,∴∠AMA′=180°-∠A′MB=180°-55°=125°,
由折叠的性质得,∠A′MN=∠AMN=∠AMA′=×125°=62.5°,故答案为:62.5.
19.【答案】解:如图所示:
【解析】(1)画直线AD,连接AD并向两方无限延长;
(2)画射线BC,以B为端点向BC方向延长交AD于点O;
(3)连接各点,其交点即为点F.
20.【答案】解:由AC=8cm,N是AC的中点,得AN=AC=4cm.
由线段的和差,得AM=AN+MN=4+6=10cm.
由M是线段AB的中点,得AB=2AM=20cm,
线段AB的长是20cm.
【解析】根据线段中点的性质,可得AN的长,根据线段的和差,可得AM的长,根据线段中点的性质,可得答案.
21.【答案】解:∵OD平分∠AOB,∠AOB=114°,∴∠AOD=∠BOD=∠AOB=57°.
∵∠BOC=2∠AOC,∠AOB=114°,∴∠AOC=∠AOB=38°.
∴∠COD=∠AOD-∠AOC=57°-38°=19°.
【解析】根据OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=114°,可以求得∠AOC、∠AOD的度数,从而可以求得∠COD的度数.
22.【答案】解:如图由折叠可知,∠EFB′=∠1=57°,∠2=20°,∠3=∠GFC′,
∵∠EFB′+∠1+∠2+∠3+∠GFC′=180°,∴∠3==23°.
【解析】根据折叠的特点可找到相等的角,在展开图中,利用∠EFB′+∠1+∠2+∠3+∠GFC′等于平角得出结论.
23.【答案】解:(1)∵OA平分∠EOC,∴∠AOC=∠EOC=×70°=35°,∴∠BOD=∠AOC=35°;
(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,∴∠AOC=∠EOC=×72°=36°,∴∠BOD=∠AOC=36°.
【解析】(1)根据角平分线定义得到∠AOC=∠EOC=×70°=35°,然后根据对顶角相等得到∠BOD=∠AOC=35°;
(2)先设∠EOC=2x,∠EOD=3x,根据平角的定义得2x+3x=180°,解得x=36°,则∠EOC=2x=72°,然后与(1)的计算方法一样.
24.【答案】解:(1)如图1,∵∠AOB=90°,∠BOC=60°,∴∠AOC=90°+60°=150°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC=75°,∠NOC=∠BOC=30°,∴∠MON=∠MOC-∠NOC=45°.
(2)如图2,∠MON=α,
理由是:∵∠AOB=α,∠BOC=60°,∴∠AOC=α+60°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC=α+30°,∠NOC=∠BOC=30°
∴∠MON=∠MOC-∠NOC=(α+30°)-30°=α.
(3)如图3,∠MON=α,与β的大小无关.
理由:∵∠AOB=α,∠BOC=β,∴∠AOC=α+β.
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=∠AOC=(α+β),∠NOC=∠BOC=β,
∴∠AON=∠AOC-∠NOC=α+β-β=α+β.
∴∠MON=∠MOC-∠NOC=(α+β)-β=α,即∠MON=α.
【解析】(1)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可;
(2)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可;
(3)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可.
25.【答案】解:(1)∵∠COE=90°,∠COE+∠AOC+∠DOE=180°,∴∠AOC+∠DOE=90°,
∵射线OF平分∠AOE,∴∠AOF=∠EOF=∠AOE,
∴∠COF=∠AOF-∠AOC=∠AOE-(90°-∠DOE)=(180°?∠DOE)?90°+∠DOE=∠DOE,
即∠AOC+∠DOE=90°,∠COF=∠DOE.
(2)数量关系:∠COF=∠DOE.
∵OF平分∠AOE,∴∠AOF=∠AOE,
∵∠COE=90°,∴∠AOC=90°-∠AOE,
∴∠COF=∠AOC+∠AOF=90°-∠AOE+∠AOE=90°-∠AOE,
∵∠AOE=180°-∠DOE,
∴∠COF=90°-(180°-∠DOE)=∠DOE,即∠COF=∠DOE;
(3)数量关系:∠COF=180°?∠DOE.
∵OF平分∠AOE,∴∠EOF=∠AOE,
∴∠COF=∠COE+∠EOF=90°+∠AOE=90°+(180°?∠DOE)=180°-∠DOE,
即∠COF=180°?∠DOE
【解析】(1)根据已知条件和图形可知:∠COE=90°,∠COE+∠AOC+∠DOE=180°,从而可以得到∠AOC与∠DOE的数量关系;由射线OF平分∠AOE,∠AOC与∠DOE的数量关系,从而可以得到∠COF和∠DOE的数量关系;
(2)由图2,可以得到各个角之间的关系,从而可以得到∠COF和∠DOE之间的数量关系;
(3)由图3和已知条件可以建立各个角之间的关系,从而可以得到∠COF和∠DOE之间的数量关系.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
