1.3.1 单调性与最大(小)值(函数的单调性的概念) 学案
文档属性
| 名称 | 1.3.1 单调性与最大(小)值(函数的单调性的概念) 学案 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-22 09:05:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
学案 函数的单调性的概念
【知识要点】
一、单调性
1.定义:如果函数y=f (x)对于属于定义域I内某个区间上的任意两个自变量的值x1、、x2,当x1、
判断单调性的方法:
(1)小题里面:①画图像;②定义法;③复合函数单调性(同增异减)
(2)大题里面:定义法,其步骤为:①取值;② 做差 ;③ 判号 ;④ 下结论.
二、单调性的有关结论
1. 调函数的定义有以下若干等价形式:设x1,x2∈[a,b],那么①>0?f(x)在[a,b]上是增函数;<0?f(x)在[a,b]上是减函数.②(x1-x2)[f(x1)-f(x2)]>0?f(x)在[a,b]上是增函数.(x1-x2)[f(x1)-f(x2)]<0?f(x)在[a,b]上是减函数.
2.若f (x), g(x)均为增(减)函数,则f (x)+g(x) 函数;
3.若f (x)为增(减)函数,则-f (x)为 ;
4.复合函数y=f [g(x)]是定义在M上的函数,若f (x)与g(x)的单调相同,则f [g(x)]为 ,若f (x), g(x)的单调性相反,则f [g(x)]为 .
说明:(1)函数的单调性也叫函数的增减性;
(2)注意区间上所取两点x1,x2的任意性;
(3)函数的单调性是对某个区间而言的,它是一个局部概念.
(4)判定函数在某个区间上的单调性的方法步骤:
a.设x1.x2∈给定区间,且x1<x2 (取值);b.计算f(x1)-f(x2)至最简(作差);
c.判断上述差的符号(断号);d.下结论(若差<0,则为增函数;若差>0,则为减函数)
(5)单调区间只能写成区间形式,不能写成集合,宁开勿闭;
(6)求单调区间先求定义域.
类型一 求函数的单调区间
【例1】下列说法不正确的有( ).
①函数y=x2在(-∞,+∞)上具有单调性.②函数的定义域为(-∞,0)∪(0,+∞),在其上是减函数;③函数y=kx+b(k∈R)在(-∞,+∞)上一定具有单调性;④若存在x1,x2是f(x)的定义域A上的两个值,当x1>x2时,有f(x1)<f(x2),则y=f(x)在A上是增函数.
A.1个 B.2个 C.3个 D.4个
【例2】求出下列函数的单调区间:
f(x)=(2)
(3) (4)=
【例3】(1).设函数f(x)=,g(x)=x2f(x﹣1),则函数g(x)的递减区间是( )
A.(﹣∞,0] B.[0,1) C.[1,+∞) D.[﹣1,0]
(2)若y=f(x)是R上的减函数,对于x1<0,x2>0,则( )
A.f(-x1)>f(-x2) B.f(-x1)<f(-x2) C.f(-x1)=f(-x2) D.无法确定
(3)若函数是定义在上的减函数,并且,则实数的取值范围为
.
类型二 证明函数单调性
【例4】(1)证明在(-∞,2]上为增函数.
(2)证明在上为增函数.
(3)证明函数在上为增函数.
(4)求证函数在上是减函数.
(5)函数f(x)=x+(a>0),在区间(0,a]上是减函数.
答案
【例1】D
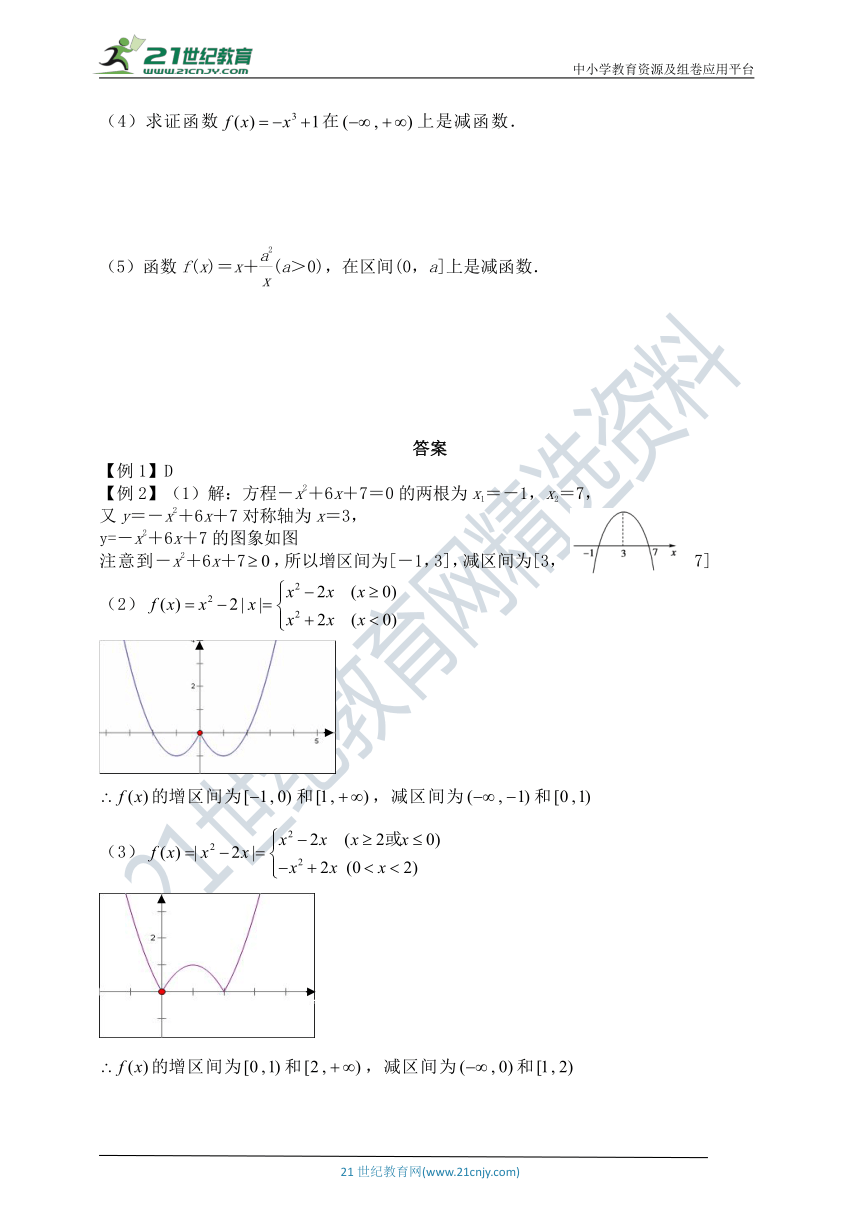
【例2】(1)解:方程-x2+6x+7=0的两根为x1=-1,x2=7,
又y=-x2+6x+7对称轴为x=3,
y=-x2+6x+7的图象如图
注意到-x2+6x+7,所以增区间为[-1,3],减区间为[3,7]
(2)
的增区间为和,减区间为和
(3)
的增区间为和,减区间为和
(4)画出f(x)=的图象如图,
可知f(x)在(-∞,0]和[1,+∞)上都是增函数,在[0,1]上是减函数.
所以f(x)的增区间为(-∞,0]和[1,+∞),减区间为[0,1]
【例3】、(1)解:由题意得,,
函数的图象如图所示,
其递减区间是[0,1).
故选:B.
由于x1<0,x2>0,所以x1<x2,则-x1>-x2,因为y=f(x)是R上的减函数,所以f(-x1)<f(-x2),故选B.
(3) 由,得,所以,即实数的取值范围为
【例4】、解:(1)设x1
∴f(x1)
f(x1)-f(x2)=-=>0.
∴f(x1)>f(x2),
∴f(x)=在[-,+∞)上为增函数.
(3)设x1>x2>-1,则
y1-y2=-=>0,
∴y1>y2,∴函数y=在(-1,+∞)上为增函数.
(4)设x1、x2∈(-∞,+∞)且x1<x2,则
f(x1)-f(x2)=(-x+1)-(-x+1)=x-x=(x2-x1)(x+x1x2+x)
∵x1<x2,∴x2-x1>0
又∵x+x1x2+x=(x1+)2+x
且(x1+)2≥0与x≥0中两等号不能同时取得(否则x1=x2=0与x1<x2矛盾),
∴x+x1x2+x>0,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
又∵x1
=(x2-x1)+=.
∵0<x1<x2≤a,∴0<x1x2<a2,∴<0,∴f(x2)<f(x1),
∴f(x)=x+(a>0)在(0,a]上是减函数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
