高中数学_ 人教A版2003课标版_ 必修3_ 古典概型和几何概型课件21张
文档属性
| 名称 | 高中数学_ 人教A版2003课标版_ 必修3_ 古典概型和几何概型课件21张 |

|
|
| 格式 | zip | ||
| 文件大小 | 225.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 17:06:57 | ||
图片预览








文档简介
课件21张PPT。古典概型和几何概型题型19 运用概率知识求随机事件发生的概率题型内容在重复抽样试验中,求随机事件发生的概率,求几何概型的概率。关键知识1.利用列举法、树状图法、列表法解决计数问题;2.古典概型概率公式,即3.几何概型概率公式,即【情形1】求无放回抽取的一个或多个事件发生的概率;
【情形2】求有放回抽取的一个或多个事件发生的概率;
【情形3】在几何区域D中随机地取一点,记事件“该点落在其内部的一个区域d内”为事件A,则事件A发生的概率。题型呈现
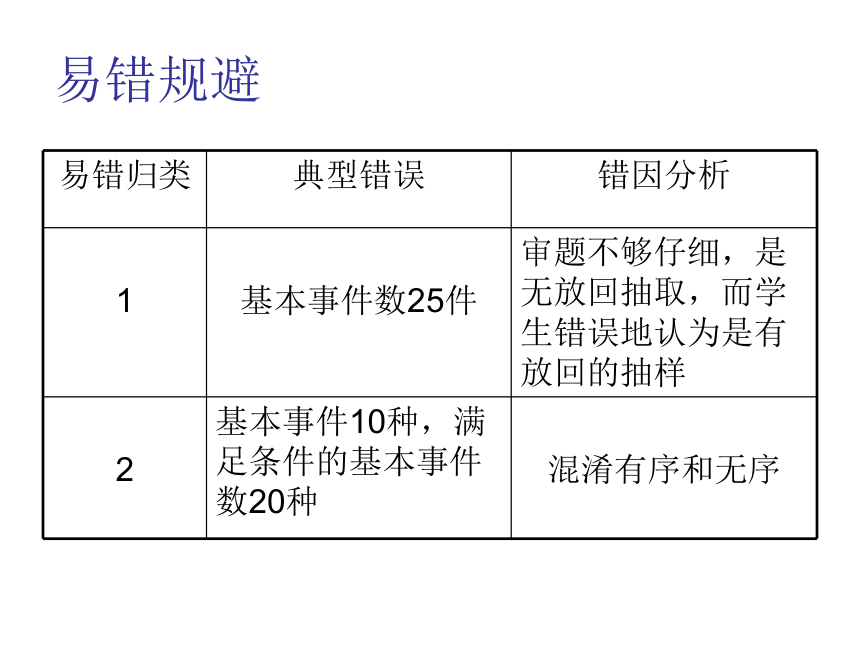
【例1】一个袋子中装有大小相同,编号分别为1,2,3,4,5的5个球,从中无放回地随机抽取2次,每次取一个球,则抽到的2个球的编号的奇偶性不同的概率为( )典例示范易错规避【例2】一个袋子中装有大小相同,编号分别为1,2,3,4,5,6,7,8的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号之和不小于15的概率为( )易错规避【例3】七巧板是我们祖先的一项创造,被誉为“东方魔板”,它是由五块等腰直角三角形(两块全等的小三角形、一块中三角形和两块全等的大三角形)、一块正方形和一块平行四边形组成的.如图是一个用七巧板拼成的正方形,在此正方形中任取一点,则此点取自阴影部分的概率是( )
易错规避题型训练1.一个不透明的袋子中装有大小相同且编号分别为1,2,3,4,5的五个小球,每次从袋中任取一个球并不放回,第一次抽取的号码记为x,第二次抽取的号码记为y,抽取的数字x,y构成一个两位数,则这个两位数是3与4的公倍数的概率是( )题型训练2.(2017全国2卷改编)
从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率是 .题型训练1.(2017山东)从分别标有1,2,3,4,5,6,7,8,9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到的2张卡片上的数奇偶性不同的概率是( )真题训练2.【2014年全国1】4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率( )真题训练3.【2018年全国1】我国数学家陈景润在歌德巴赫猜想的研究中取得了世界领先的成果.歌德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )
真题训练4.【2016年全国1】某公司的班车在7:30 ,8:00 ,8:30 发车,小明在 7:50至8:30 之间到达发车站乘坐班车,且到达发车站的时候是随机的,则他等车时间不超过10分钟的概率是( )真题训练5.【2017年全国1】如图,正方形ABCD内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
真题训练 6.【2018年全国1】下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则
A.p1=p2 B.p1=p3
C.p2=p3 D.p1=p2+p3例4 一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4. (1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率; (2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n
【情形2】求有放回抽取的一个或多个事件发生的概率;
【情形3】在几何区域D中随机地取一点,记事件“该点落在其内部的一个区域d内”为事件A,则事件A发生的概率。题型呈现
【例1】一个袋子中装有大小相同,编号分别为1,2,3,4,5的5个球,从中无放回地随机抽取2次,每次取一个球,则抽到的2个球的编号的奇偶性不同的概率为( )典例示范易错规避【例2】一个袋子中装有大小相同,编号分别为1,2,3,4,5,6,7,8的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号之和不小于15的概率为( )易错规避【例3】七巧板是我们祖先的一项创造,被誉为“东方魔板”,它是由五块等腰直角三角形(两块全等的小三角形、一块中三角形和两块全等的大三角形)、一块正方形和一块平行四边形组成的.如图是一个用七巧板拼成的正方形,在此正方形中任取一点,则此点取自阴影部分的概率是( )
易错规避题型训练1.一个不透明的袋子中装有大小相同且编号分别为1,2,3,4,5的五个小球,每次从袋中任取一个球并不放回,第一次抽取的号码记为x,第二次抽取的号码记为y,抽取的数字x,y构成一个两位数,则这个两位数是3与4的公倍数的概率是( )题型训练2.(2017全国2卷改编)
从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率是 .题型训练1.(2017山东)从分别标有1,2,3,4,5,6,7,8,9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到的2张卡片上的数奇偶性不同的概率是( )真题训练2.【2014年全国1】4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率( )真题训练3.【2018年全国1】我国数学家陈景润在歌德巴赫猜想的研究中取得了世界领先的成果.歌德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )
真题训练4.【2016年全国1】某公司的班车在7:30 ,8:00 ,8:30 发车,小明在 7:50至8:30 之间到达发车站乘坐班车,且到达发车站的时候是随机的,则他等车时间不超过10分钟的概率是( )真题训练5.【2017年全国1】如图,正方形ABCD内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
真题训练 6.【2018年全国1】下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则
A.p1=p2 B.p1=p3
C.p2=p3 D.p1=p2+p3例4 一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4. (1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率; (2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n
