陕西省咸阳市2018-2019学年高一下学期期末教学质量检测数学试题
文档属性
| 名称 | 陕西省咸阳市2018-2019学年高一下学期期末教学质量检测数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 869.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 07:55:58 | ||
图片预览


文档简介
咸阳市2018-2019学年高一下学期期末考试
数学试卷
满分150分,考试时间120分钟
第I卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小剧给出的四个选项中,只有一项是符合题目要求的
1.已知x,y是两个变量,下列四个散点图中,x,y呈负相关趋势的是( )
2.下列叙述中,不能称为算法的是( )
A、植树需要运苗、挖坑、栽苗、浇水这些步骤
B、按顺序进行下列运算:1+1=2,2+1=3,3+1=4,…,99+1=100
C、从济南到北京旅游,先坐火车,再坐飞机抵达
D、3x>x+1
3.式子coscos-sinsin的值为( )
A、- B、0 C、1 D、-
4.在四边形ABCD中,若,=0,则四边形ABCD的形状一定是( )
A、矩形 B、正方形 C、菱形 D、直角梯形
5.函数y=tan()的定义域是( )
A、{x|x≠2kπ+,k∈Z} B、{x|x≠4kπ+,k∈Z}
C、{x|x≠,k∈Z} D、{x|x≠kπ+,k∈Z}
6.已知扇形的周长为8cm,圆心角为2弧度,则该扇形的面积为( )
A、16cm2 B、8 cm2 C、4 cm2 D、2 cm2
7.已知α是第二象限角,且sinα=,则tan2α的值为( )
A、 B、﹣ C、﹣ D、﹣
8.从装有红球和绿球的口袋内任取2个球(已知口袋中的红球、绿球数都大于2),那么互斥而不对立的两个事件是( )
A、至少有一个是红球,至少有一个是绿球
B、恰有一个红球,恰有两个绿球
C、至少有一个红球,都是红球
D、至少有一个红球,都是绿球
9.在区间[﹣1,1]上任选两个数x和y,则x2+y2≥1的概率为( )
A、1- B、- C、1- D、
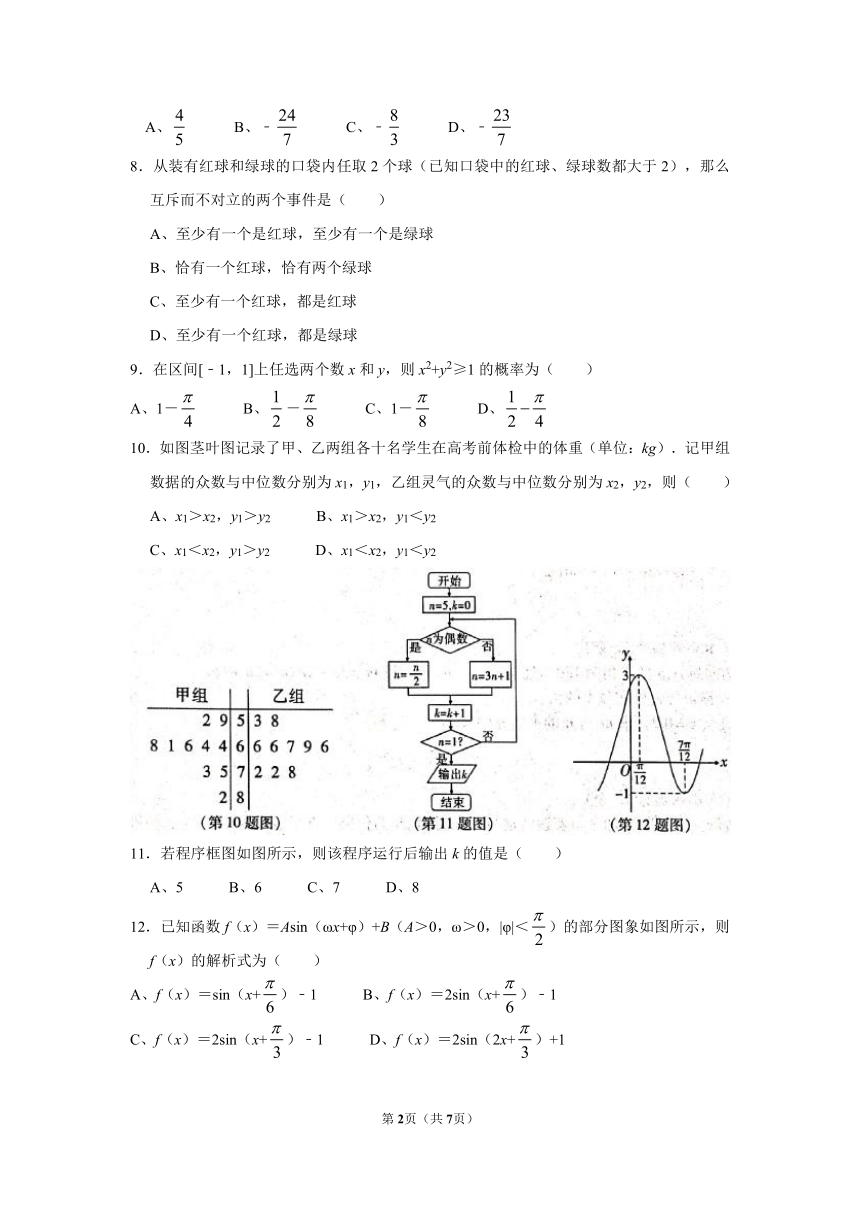
10.如图茎叶图记录了甲、乙两组各十名学生在高考前体检中的体重(单位:kg).记甲组数据的众数与中位数分别为x1,y1,乙组灵气的众数与中位数分别为x2,y2,则( )
A、x1>x2,y1>y2 B、x1>x2,y1<y2
C、x1<x2,y1>y2 D、x1<x2,y1<y2
11.若程序框图如图所示,则该程序运行后输出k的值是( )
A、5 B、6 C、7 D、8
12.已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<)的部分图象如图所示,则f(x)的解析式为( )
A、f(x)=sin(x+)﹣1 B、f(x)=2sin(x+)﹣1
C、f(x)=2sin(x+)﹣1 D、f(x)=2sin(2x+)+1
第II卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13.已知向量a=(1,2),b=(x,4),且a∥b,则|a﹣b|= .
14.某中学高一年级有学生1200人,高二年级有学生900人,高三年级有学生1500人,现按年级用分层抽样的方法从这三个年级的学生中抽取一个容量为720的样本进行某项研究,则应从高三年级学生中抽取 人.
15.某产品分为优质品、合格品、次品三个等级生产中出现合格品的概率为0.25,出现次品的概率为0.03.则对该产品抽査一次,抽得优质品的概率是 .
16.将函数f(x)=cos(2x+)的图象向左平移个单位长度后,得到函数g(x)的图象,则下列结论中正确的是 .(填所有正确结论的序号)
①g(x)的最小正周期为4π;
②g(x)在区间[0,]上单调递减;
③g(x)图象的一条对称轴为x=;
④g(x)图象的一个对称中心为(,0).
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤
17.(10分)已知角α的终边经过点P(m,2),且cosα=-.
(1)求m的值;
(2)求的值.
18.(12分)已知向量a,b的夹角为120°,且|a|=2,| b |=3,设m=3a-2 b,n=2a+k b.
(Ⅰ)若m⊥m,求实数k的值;
(Ⅱ)当k=0时,求m与m的夹角θ的大小.
19.(12分)为选派一名学生参加全市实践活动技能竟赛,A、B两位同学在学校的学习基地现场进行加工直径为20mm的零件测试,他俩各加工的10个零件直径的相关数据如图所示(单位:mm)
A、B两位同学各加工的10个零件直径的平均数与方差列于下表;
根据测试得到的有关数据,试解答下列问题:
(Ⅰ)计算s2B,考虑平均数与方差,说明谁的成绩好些;
(Ⅱ)考虑图中折线走势情况,你认为派谁去参赛较合适?请说明你的理由.
20.(12分)某超市为了解端午节期间粽子的销售量,对其所在销售范围内的1000名消费者在端午节期间的粽子购买量(单位:g)进行了问卷调查,得到如图所示的频率分布直方图.
(Ⅰ)求频率分布直方图中a的值;
(Ⅱ)求这1000名消费者的棕子购买量在600g~1400g的人数;
(Ⅲ)求这1000名消费者的人均粽子购买量(频率分布直方图中同一组的数据用该组区间的中点值作代表).
21.(12分)已知函数f(x)=sin2ωx+sinωxcosωx(ω>0)的最小正周期为π.
(Ⅰ)求ω的值和f(x)的单调递增区间;
(Ⅱ)若关于x的方程f(x)﹣m=0在区间[0,]上有两个实数解,求实数m的取值范围.
22.(12分)某市食品药品监督管理局开展2019年春季校园餐饮安全检查,对本市的8所中学食堂进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如表所示:
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;(精确到0.1)
(2)现从8个被检查的中学食堂中任意抽取两个组成一组,若两个中学食堂的原料采购加工标准和卫生标准的评分均超过80分,则组成“对比标兵食堂”,求该组被评为“对比标兵食堂”的概率.
数学试卷
满分150分,考试时间120分钟
第I卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小剧给出的四个选项中,只有一项是符合题目要求的
1.已知x,y是两个变量,下列四个散点图中,x,y呈负相关趋势的是( )
2.下列叙述中,不能称为算法的是( )
A、植树需要运苗、挖坑、栽苗、浇水这些步骤
B、按顺序进行下列运算:1+1=2,2+1=3,3+1=4,…,99+1=100
C、从济南到北京旅游,先坐火车,再坐飞机抵达
D、3x>x+1
3.式子coscos-sinsin的值为( )
A、- B、0 C、1 D、-
4.在四边形ABCD中,若,=0,则四边形ABCD的形状一定是( )
A、矩形 B、正方形 C、菱形 D、直角梯形
5.函数y=tan()的定义域是( )
A、{x|x≠2kπ+,k∈Z} B、{x|x≠4kπ+,k∈Z}
C、{x|x≠,k∈Z} D、{x|x≠kπ+,k∈Z}
6.已知扇形的周长为8cm,圆心角为2弧度,则该扇形的面积为( )
A、16cm2 B、8 cm2 C、4 cm2 D、2 cm2
7.已知α是第二象限角,且sinα=,则tan2α的值为( )
A、 B、﹣ C、﹣ D、﹣
8.从装有红球和绿球的口袋内任取2个球(已知口袋中的红球、绿球数都大于2),那么互斥而不对立的两个事件是( )
A、至少有一个是红球,至少有一个是绿球
B、恰有一个红球,恰有两个绿球
C、至少有一个红球,都是红球
D、至少有一个红球,都是绿球
9.在区间[﹣1,1]上任选两个数x和y,则x2+y2≥1的概率为( )
A、1- B、- C、1- D、
10.如图茎叶图记录了甲、乙两组各十名学生在高考前体检中的体重(单位:kg).记甲组数据的众数与中位数分别为x1,y1,乙组灵气的众数与中位数分别为x2,y2,则( )
A、x1>x2,y1>y2 B、x1>x2,y1<y2
C、x1<x2,y1>y2 D、x1<x2,y1<y2
11.若程序框图如图所示,则该程序运行后输出k的值是( )
A、5 B、6 C、7 D、8
12.已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<)的部分图象如图所示,则f(x)的解析式为( )
A、f(x)=sin(x+)﹣1 B、f(x)=2sin(x+)﹣1
C、f(x)=2sin(x+)﹣1 D、f(x)=2sin(2x+)+1
第II卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13.已知向量a=(1,2),b=(x,4),且a∥b,则|a﹣b|= .
14.某中学高一年级有学生1200人,高二年级有学生900人,高三年级有学生1500人,现按年级用分层抽样的方法从这三个年级的学生中抽取一个容量为720的样本进行某项研究,则应从高三年级学生中抽取 人.
15.某产品分为优质品、合格品、次品三个等级生产中出现合格品的概率为0.25,出现次品的概率为0.03.则对该产品抽査一次,抽得优质品的概率是 .
16.将函数f(x)=cos(2x+)的图象向左平移个单位长度后,得到函数g(x)的图象,则下列结论中正确的是 .(填所有正确结论的序号)
①g(x)的最小正周期为4π;
②g(x)在区间[0,]上单调递减;
③g(x)图象的一条对称轴为x=;
④g(x)图象的一个对称中心为(,0).
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤
17.(10分)已知角α的终边经过点P(m,2),且cosα=-.
(1)求m的值;
(2)求的值.
18.(12分)已知向量a,b的夹角为120°,且|a|=2,| b |=3,设m=3a-2 b,n=2a+k b.
(Ⅰ)若m⊥m,求实数k的值;
(Ⅱ)当k=0时,求m与m的夹角θ的大小.
19.(12分)为选派一名学生参加全市实践活动技能竟赛,A、B两位同学在学校的学习基地现场进行加工直径为20mm的零件测试,他俩各加工的10个零件直径的相关数据如图所示(单位:mm)
A、B两位同学各加工的10个零件直径的平均数与方差列于下表;
根据测试得到的有关数据,试解答下列问题:
(Ⅰ)计算s2B,考虑平均数与方差,说明谁的成绩好些;
(Ⅱ)考虑图中折线走势情况,你认为派谁去参赛较合适?请说明你的理由.
20.(12分)某超市为了解端午节期间粽子的销售量,对其所在销售范围内的1000名消费者在端午节期间的粽子购买量(单位:g)进行了问卷调查,得到如图所示的频率分布直方图.
(Ⅰ)求频率分布直方图中a的值;
(Ⅱ)求这1000名消费者的棕子购买量在600g~1400g的人数;
(Ⅲ)求这1000名消费者的人均粽子购买量(频率分布直方图中同一组的数据用该组区间的中点值作代表).
21.(12分)已知函数f(x)=sin2ωx+sinωxcosωx(ω>0)的最小正周期为π.
(Ⅰ)求ω的值和f(x)的单调递增区间;
(Ⅱ)若关于x的方程f(x)﹣m=0在区间[0,]上有两个实数解,求实数m的取值范围.
22.(12分)某市食品药品监督管理局开展2019年春季校园餐饮安全检查,对本市的8所中学食堂进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如表所示:
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;(精确到0.1)
(2)现从8个被检查的中学食堂中任意抽取两个组成一组,若两个中学食堂的原料采购加工标准和卫生标准的评分均超过80分,则组成“对比标兵食堂”,求该组被评为“对比标兵食堂”的概率.
同课章节目录
