人教版八年级数学上册13.2 画轴对称图形 同步测试题(有答案)
文档属性
| 名称 | 人教版八年级数学上册13.2 画轴对称图形 同步测试题(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 453.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-23 00:00:00 | ||
图片预览

文档简介
人教版八年级数学上册 第13章 轴对称 13.2 画轴对称图形 同步测试
一.选择题(共10小题,每小题3分,共30分)
1.点P(﹣3,2)关于x轴的对称点的坐标为( )
A.(﹣3,﹣2) B.(3,﹣2) C.(2,﹣3) D.(﹣2,﹣3)
2.如果点P(2,b)和点Q(a,﹣3)关于x轴对称,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
3.在平面直角坐标系中,作点A(3,4)关于x轴对称的点A′,再将点A′向左平移6个单位,得到点B,则点B的坐标为( )
A.(4,﹣3) B.(﹣4,3) C.(﹣3,4) D.(﹣3,﹣4)
4.在平面直角坐标系中,点P(﹣2018,2019)关于y轴对称点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,A(a,b)(b≠0),B(m,n).若a﹣m=4,b+n=0,则下列结论正确的是( )
A.把点A向左平移4个单位长度后,与点B关于x轴对称
B.把点A向右平移4个单位长度后,与点B关于x轴对称
C.把点A向左平移4个单位长度后,与点B关于y轴对称
D.把点A向右平移4个单位长度后,与点B关于y轴对称
6.嘉嘉和淇淇下棋,嘉嘉执圆形棋子,淇淇执方形棋子,如图,棋盘中心的圆形棋子的位置用(﹣1,1)表示,右下角的圆形棋子用(0,0)表示,淇淇将第4枚方形棋子放入棋盘后,所有棋子构成的图形是轴对称图形.则淇淇放的方形棋子的位置可能是( )
A.(﹣1,2) B.(﹣1,﹣1) C.(0,2) D.(1,3)
7.若点A(1,2),B(﹣1,2),则点A与点B的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于直线x=1对称 D.关于直线y=1对称
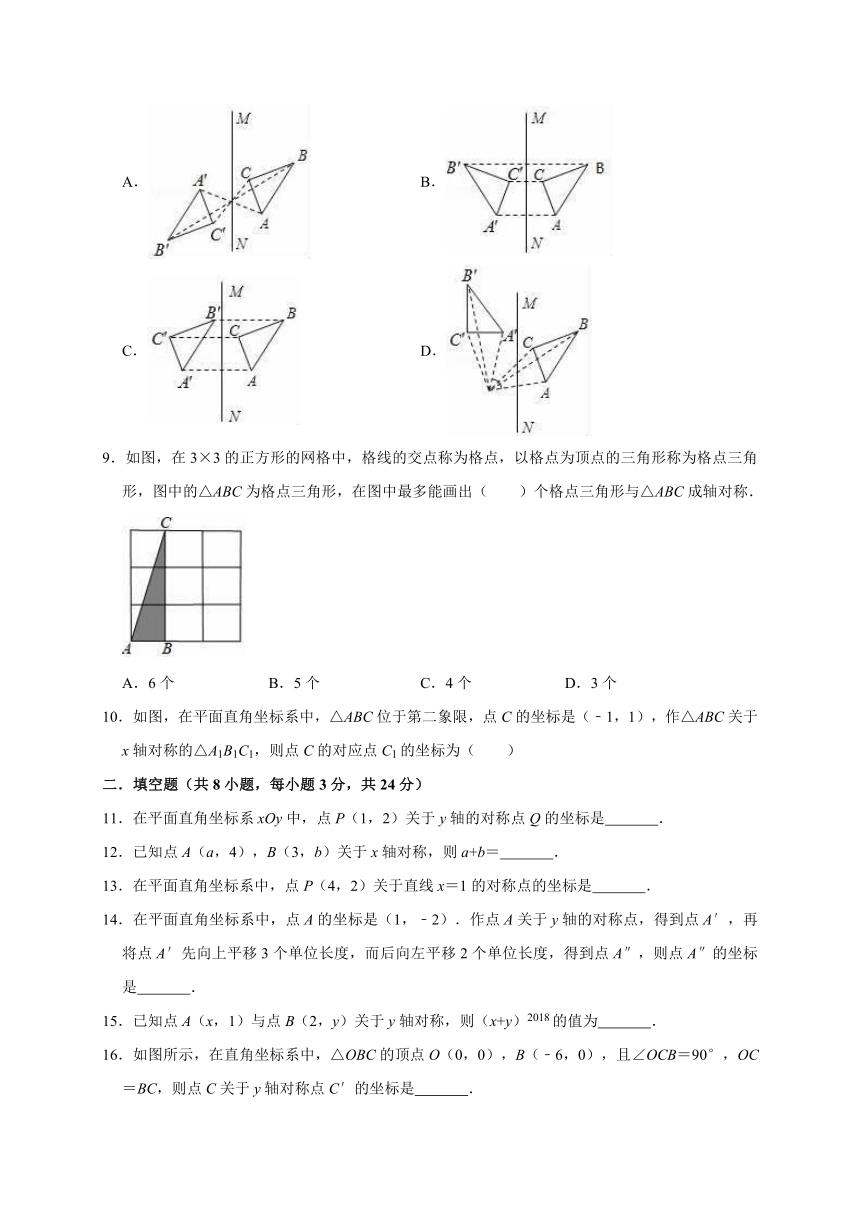
8.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A. B.
C. D.
9.如图,在3×3的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中最多能画出( )个格点三角形与△ABC成轴对称.
A.6个 B.5个 C.4个 D.3个
10.如图,在平面直角坐标系中,△ABC位于第二象限,点C的坐标是(﹣1,1),作△ABC关于x轴对称的△A1B1C1,则点C的对应点C1的坐标为( )
二.填空题(共8小题,每小题3分,共24分)
11.在平面直角坐标系xOy中,点P(1,2)关于y轴的对称点Q的坐标是 .
12.已知点A(a,4),B(3,b)关于x轴对称,则a+b= .
13.在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是 .
14.在平面直角坐标系中,点A的坐标是(1,﹣2).作点A关于y轴的对称点,得到点A′,再将点A′先向上平移3个单位长度,而后向左平移2个单位长度,得到点A″,则点A″的坐标是 .
15.已知点A(x,1)与点B(2,y)关于y轴对称,则(x+y)2018的值为 .
16.如图所示,在直角坐标系中,△OBC的顶点O(0,0),B(﹣6,0),且∠OCB=90°,OC=BC,则点C关于y轴对称点C′的坐标是 .
17.已知点A(﹣3,0),B(5,4),点P是线段AB的中点,P与Q关于x轴对称,则Q点坐标是 .
18.已知点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,则m的取值范围是 .
A.(1,1) B.(1,﹣1) C.(﹣1,1) D.(﹣1,﹣1)
三.解答题(共7小题,共66分)
19.已知点M(m﹣1,1﹣2m)关于y轴的对称点在第一象限,求m的取值范围,并在数轴上表示出来.
20.(1)利用平面直角坐标系,分别写出点(2,2),(﹣2,3),(4,﹣1)关于直线x=1的对称点的坐标;
(2)分别写出(1)中各点关于直线x=﹣1的对称点的坐标;
(3)写出点(a,b)关于直线x=m的对称点的坐标.
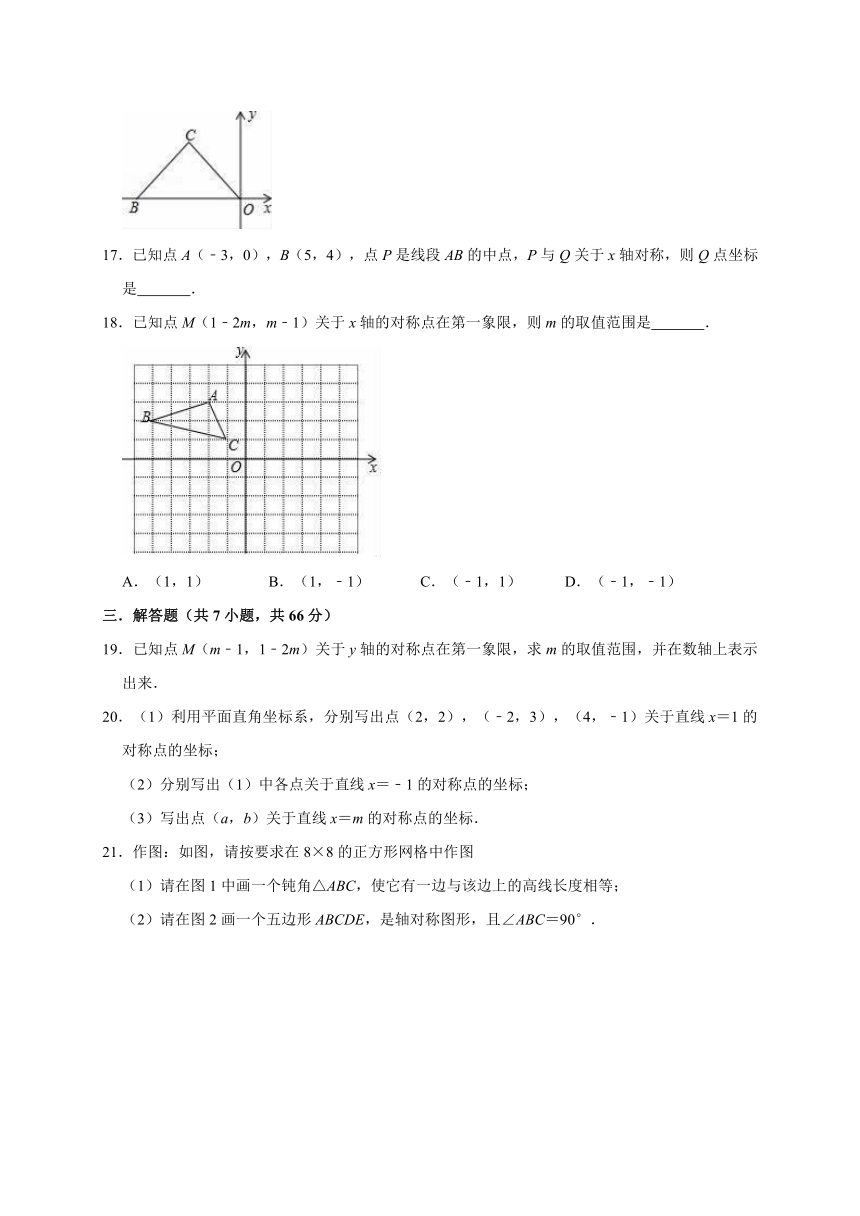
21.作图:如图,请按要求在8×8的正方形网格中作图
(1)请在图1中画一个钝角△ABC,使它有一边与该边上的高线长度相等;
(2)请在图2画一个五边形ABCDE,是轴对称图形,且∠ABC=90°.
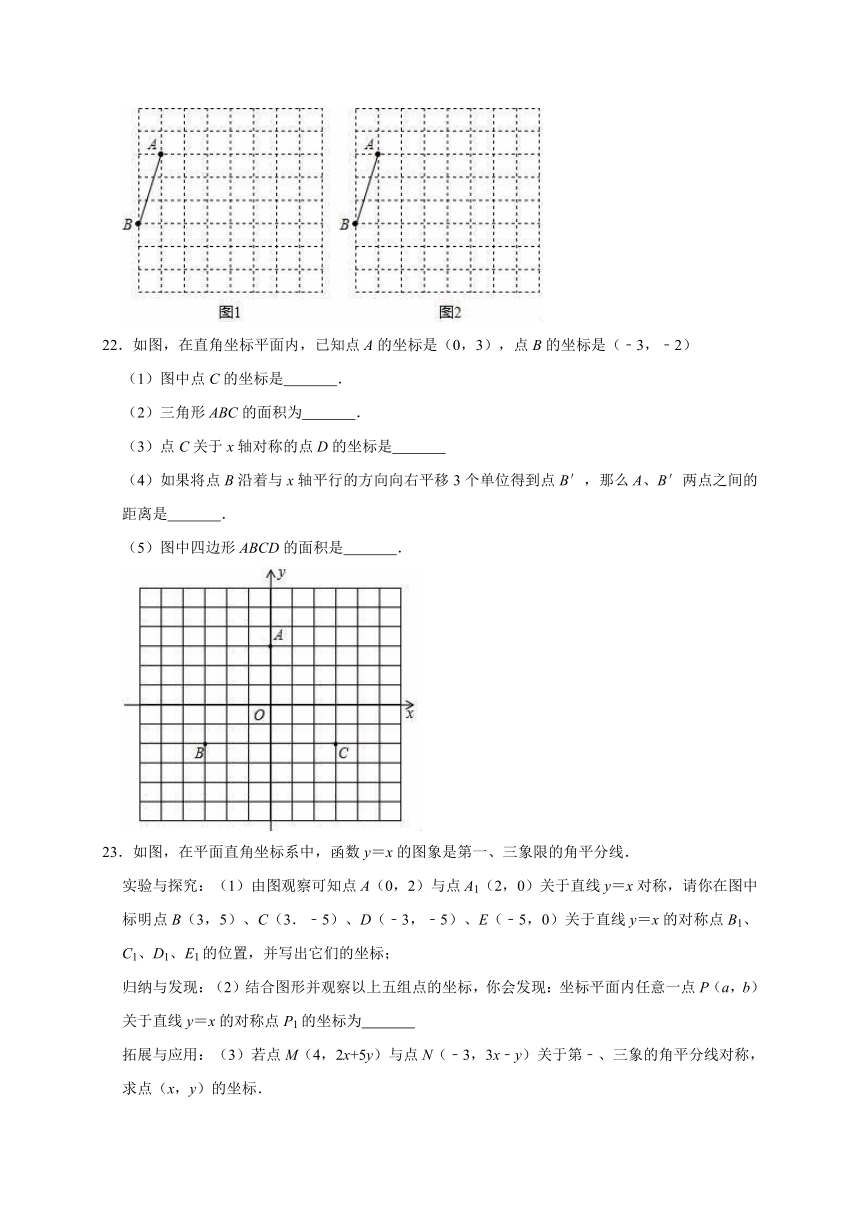
22.如图,在直角坐标平面内,已知点A的坐标是(0,3),点B的坐标是(﹣3,﹣2)
(1)图中点C的坐标是 .
(2)三角形ABC的面积为 .
(3)点C关于x轴对称的点D的坐标是
(4)如果将点B沿着与x轴平行的方向向右平移3个单位得到点B′,那么A、B′两点之间的距离是 .
(5)图中四边形ABCD的面积是 .
23.如图,在平面直角坐标系中,函数y=x的图象是第一、三象限的角平分线.
实验与探究:(1)由图观察可知点A(0,2)与点A1(2,0)关于直线y=x对称,请你在图中标明点B(3,5)、C(3.﹣5)、D(﹣3,﹣5)、E(﹣5,0)关于直线y=x的对称点B1、C1、D1、E1的位置,并写出它们的坐标;
归纳与发现:(2)结合图形并观察以上五组点的坐标,你会发现:坐标平面内任意一点P(a,b)关于直线y=x的对称点P1的坐标为
拓展与应用:(3)若点M(4,2x+5y)与点N(﹣3,3x﹣y)关于第﹣、三象的角平分线对称,求点(x,y)的坐标.
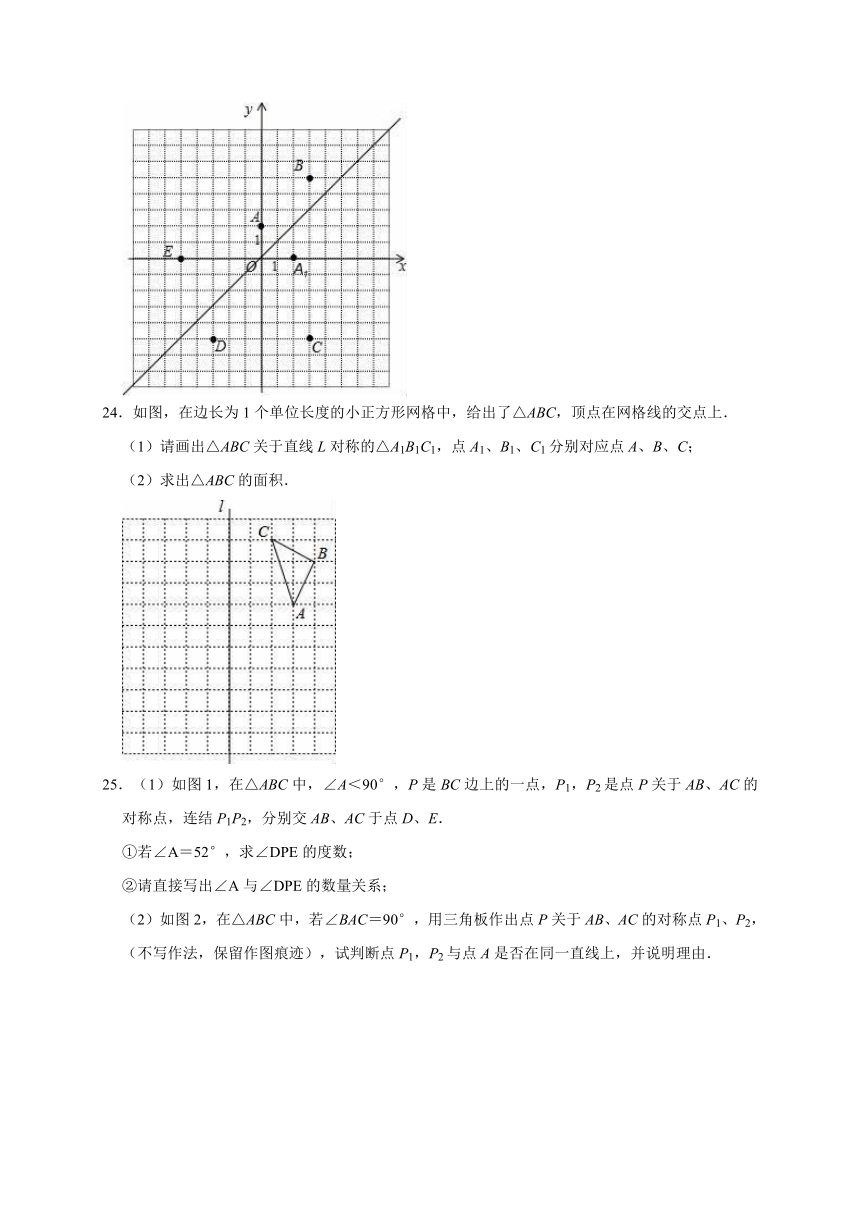
24.如图,在边长为1个单位长度的小正方形网格中,给出了△ABC,顶点在网格线的交点上.
(1)请画出△ABC关于直线L对称的△A1B1C1,点A1、B1、C1分别对应点A、B、C;
(2)求出△ABC的面积.
25.(1)如图1,在△ABC中,∠A<90°,P是BC边上的一点,P1,P2是点P关于AB、AC的对称点,连结P1P2,分别交AB、AC于点D、E.
①若∠A=52°,求∠DPE的度数;
②请直接写出∠A与∠DPE的数量关系;
(2)如图2,在△ABC中,若∠BAC=90°,用三角板作出点P关于AB、AC的对称点P1、P2,(不写作法,保留作图痕迹),试判断点P1,P2与点A是否在同一直线上,并说明理由.
参考答案
一.选择题
1.解:点P(﹣3,2)关于x轴的对称点的坐标是(﹣3,﹣2).
故选:A.
2.解:∵点P(2,b)和点Q(a,﹣3)关于x轴对称,
∴a=2,b=3,
则a+b的值是:5.
故选:D.
3.解:A(3,4)关于x轴对称的点A′(3,﹣4),将点A′向左平移6个单位,得到点B(﹣3,﹣4),
故选:D.
4.解:∵点P(﹣2018,2019)关于y轴的对称点为(2018,2019),
∴对称点一定在第一象限.
故选:A.
5.解:∵a﹣m=4,∴a﹣4=m,
又∵b+n=0(b≠0),
∴b=﹣n,
∴把点A向左平移4个单位长度后,与点B关于x轴对称.
故选:A.
6.解:
故选:A.
7.解:∵点A(1,2),B(﹣1,2),
∴点A与点B关于y轴对称,
故选:B.
8.解:作△ABC关于直线MN的轴对称图形正确的是B选项,
故选:B.
9.解:如图,最多能画出6个格点三角形与△ABC成轴对称.
故选:A.
10.解:∵点C的坐标是(﹣1,1),作△ABC关于x轴对称的△A1B1C1,
∴点C的对应点C1的坐标为:(﹣1,﹣1).
故选:D.
二.填空题
11.解:点P(1,2)关于y轴的对称点Q的坐标是:(﹣1,2).
故答案为:(﹣1,2).
12.解:∵点A(a,4)、点B(3,b)关于x轴对称,
∴a=3,b=﹣4,
∴a+b=﹣1,
故答案为:﹣1.
13.解:∵点P(4,2),
∴点P到直线x=1的距离为4﹣1=3,∴点P关于直线x=1的对称点P′到直线x=1的距离为3,
∴点P′的横坐标为1﹣3=﹣2,
∴对称点P′的坐标为(﹣2,2).
故答案为:(﹣2,2).
14.解:∵点A的坐标是(1,﹣2),
∴点A关于y轴的对称点A′(﹣1,﹣2),
∵将点A′先向上平移3个单位长度,而后向左平移2个单位长度,得到点A″,
∴点A″的坐标是(﹣1﹣2,﹣2+3),
即(﹣3,1),
故答案为:(﹣3,1).
15.解:∵点A(x,1)与点B(2,y)关于y轴对称,
∴x=﹣2,y=1,
故(x+y)2018=(﹣2+1)2018=1.
故答案为:1.
16.解:如图,过点C作CD⊥OB于D,
∵∠OCB=90°,OC=BC,
∴△BOC是等腰直角三角形,
∴CD=OD=OB,
∵O(0,0),B(﹣6,0),
∴OB=6,
∴CD=OD=×6=3,
∴点C的坐标为(﹣3,3),
∴点C关于y轴对称点C′的坐标是(3,3).
故答案为:(3,3).
17.解:∵A(﹣3,0),B(5,4),点P是线段AB的中点,
∴P(,),即P(1,2),
又∵P与Q关于x轴对称,
∴Q点坐标是(1,﹣2),
故答案为:(1,﹣2).
18.解:∵点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,
∴点M在第四象限,
∴,
解得:m<.
故答案为:m<.
三.解答题
19.解:由题意,得
M在第四象限,得
m﹣1>0,1﹣2m<0,
解得m>1,
在数轴上表示如图.
20.解:(1)如图,点(2,2),(﹣2,3),(4,﹣1)关于直线x=1的对称点的坐标分别为(0,2),(4,3),(﹣2,﹣1);
(2)如图,点(2,2),(﹣2,3),(4,﹣1)关于直线x=﹣1的对称点的坐标分别为(﹣4,2),(0,3),(﹣6,﹣1);
(3)点(a,b)关于直线x=m的对称点的坐标为(2m﹣a,b).
21.解:(1)
(2)
22.解:(1)根据题意得点C的坐标为(3,﹣2);
故答案为:(3,﹣2);
(2)△ABC的面积:.
故答案为:15;
(3)点C关于x轴对称的点D的坐标是(3,2);
故答案为:(3,2);
(4)将点B沿着与x轴平行的方向向右平移3个单位得到点B′(﹣3+3,﹣2),即(0,﹣2),
A、B′两点之间的距离是:3﹣(﹣2)=5;
故答案为:5;
(5),
∴四边形ABCD的面积为:S△ABC+S△ACD=15+6=21.
故答案为:21
23.解:(1)由图观察可知B1(5,3),C1、(﹣5,3),D1(﹣5,﹣3),E1(0,﹣5);
(2)结合图形并观察以上五组点的坐标,你会发现:坐标平面内任意一点P(a,b)关于直线y=x的对称点P1的坐标为 (b,a).
故答案为(b,a).
(3)根据任意一点P(a,b)关于直线y=x的对称点P1的坐标为 (b,a)可知,
解得.
所以点(x,y)的坐标为(1,﹣1).
24.解:(1)如图所示,△A1B1C1即为所求.
(2)△ABC的面积为2×3﹣×1×3﹣×1×2﹣×1×2=.
25.解:(1)①∵P1,P2是点P关于AB、AC的对称点,
∴PD=P1D,PE=P2E,
∴∠EDP=2∠DPP1,∠DEP=2∠EPP2,
∵∠DPP1+∠DPE+∠EPP2+∠A=180° ①,
2∠DPP1+∠DPE+2∠EPP2=180° ②
②﹣①得:∠DPP1+∠EPP2=∠A,
∵∠A=52°,
∴∠DPP1+∠EPP2=52°,
∴∠DPE=180°﹣(∠PDE+∠DEF)
=180°﹣2(∠DPP1+∠EPP2)
=180°﹣104°=76°.
(2)由(1)可知:∠DPE=180°﹣2∠A.
(3)点P1,P2与点A在同一条直线上.
理由如下:连接AP,AP1,AP2.
根据轴对称的性质,可得∠4=∠1,∠3=∠2,
∵∠BAC=90°,
即∠1+∠2=90°,
∴∠3+∠4=90°,
∴∠1+∠2+∠3+∠4=180°,
即∠P1AP2=180°,
∴点P1,P2与点A在同一条直线上.
一.选择题(共10小题,每小题3分,共30分)
1.点P(﹣3,2)关于x轴的对称点的坐标为( )
A.(﹣3,﹣2) B.(3,﹣2) C.(2,﹣3) D.(﹣2,﹣3)
2.如果点P(2,b)和点Q(a,﹣3)关于x轴对称,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
3.在平面直角坐标系中,作点A(3,4)关于x轴对称的点A′,再将点A′向左平移6个单位,得到点B,则点B的坐标为( )
A.(4,﹣3) B.(﹣4,3) C.(﹣3,4) D.(﹣3,﹣4)
4.在平面直角坐标系中,点P(﹣2018,2019)关于y轴对称点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,A(a,b)(b≠0),B(m,n).若a﹣m=4,b+n=0,则下列结论正确的是( )
A.把点A向左平移4个单位长度后,与点B关于x轴对称
B.把点A向右平移4个单位长度后,与点B关于x轴对称
C.把点A向左平移4个单位长度后,与点B关于y轴对称
D.把点A向右平移4个单位长度后,与点B关于y轴对称
6.嘉嘉和淇淇下棋,嘉嘉执圆形棋子,淇淇执方形棋子,如图,棋盘中心的圆形棋子的位置用(﹣1,1)表示,右下角的圆形棋子用(0,0)表示,淇淇将第4枚方形棋子放入棋盘后,所有棋子构成的图形是轴对称图形.则淇淇放的方形棋子的位置可能是( )
A.(﹣1,2) B.(﹣1,﹣1) C.(0,2) D.(1,3)
7.若点A(1,2),B(﹣1,2),则点A与点B的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于直线x=1对称 D.关于直线y=1对称
8.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A. B.
C. D.
9.如图,在3×3的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中最多能画出( )个格点三角形与△ABC成轴对称.
A.6个 B.5个 C.4个 D.3个
10.如图,在平面直角坐标系中,△ABC位于第二象限,点C的坐标是(﹣1,1),作△ABC关于x轴对称的△A1B1C1,则点C的对应点C1的坐标为( )
二.填空题(共8小题,每小题3分,共24分)
11.在平面直角坐标系xOy中,点P(1,2)关于y轴的对称点Q的坐标是 .
12.已知点A(a,4),B(3,b)关于x轴对称,则a+b= .
13.在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是 .
14.在平面直角坐标系中,点A的坐标是(1,﹣2).作点A关于y轴的对称点,得到点A′,再将点A′先向上平移3个单位长度,而后向左平移2个单位长度,得到点A″,则点A″的坐标是 .
15.已知点A(x,1)与点B(2,y)关于y轴对称,则(x+y)2018的值为 .
16.如图所示,在直角坐标系中,△OBC的顶点O(0,0),B(﹣6,0),且∠OCB=90°,OC=BC,则点C关于y轴对称点C′的坐标是 .
17.已知点A(﹣3,0),B(5,4),点P是线段AB的中点,P与Q关于x轴对称,则Q点坐标是 .
18.已知点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,则m的取值范围是 .
A.(1,1) B.(1,﹣1) C.(﹣1,1) D.(﹣1,﹣1)
三.解答题(共7小题,共66分)
19.已知点M(m﹣1,1﹣2m)关于y轴的对称点在第一象限,求m的取值范围,并在数轴上表示出来.
20.(1)利用平面直角坐标系,分别写出点(2,2),(﹣2,3),(4,﹣1)关于直线x=1的对称点的坐标;
(2)分别写出(1)中各点关于直线x=﹣1的对称点的坐标;
(3)写出点(a,b)关于直线x=m的对称点的坐标.
21.作图:如图,请按要求在8×8的正方形网格中作图
(1)请在图1中画一个钝角△ABC,使它有一边与该边上的高线长度相等;
(2)请在图2画一个五边形ABCDE,是轴对称图形,且∠ABC=90°.
22.如图,在直角坐标平面内,已知点A的坐标是(0,3),点B的坐标是(﹣3,﹣2)
(1)图中点C的坐标是 .
(2)三角形ABC的面积为 .
(3)点C关于x轴对称的点D的坐标是
(4)如果将点B沿着与x轴平行的方向向右平移3个单位得到点B′,那么A、B′两点之间的距离是 .
(5)图中四边形ABCD的面积是 .
23.如图,在平面直角坐标系中,函数y=x的图象是第一、三象限的角平分线.
实验与探究:(1)由图观察可知点A(0,2)与点A1(2,0)关于直线y=x对称,请你在图中标明点B(3,5)、C(3.﹣5)、D(﹣3,﹣5)、E(﹣5,0)关于直线y=x的对称点B1、C1、D1、E1的位置,并写出它们的坐标;
归纳与发现:(2)结合图形并观察以上五组点的坐标,你会发现:坐标平面内任意一点P(a,b)关于直线y=x的对称点P1的坐标为
拓展与应用:(3)若点M(4,2x+5y)与点N(﹣3,3x﹣y)关于第﹣、三象的角平分线对称,求点(x,y)的坐标.
24.如图,在边长为1个单位长度的小正方形网格中,给出了△ABC,顶点在网格线的交点上.
(1)请画出△ABC关于直线L对称的△A1B1C1,点A1、B1、C1分别对应点A、B、C;
(2)求出△ABC的面积.
25.(1)如图1,在△ABC中,∠A<90°,P是BC边上的一点,P1,P2是点P关于AB、AC的对称点,连结P1P2,分别交AB、AC于点D、E.
①若∠A=52°,求∠DPE的度数;
②请直接写出∠A与∠DPE的数量关系;
(2)如图2,在△ABC中,若∠BAC=90°,用三角板作出点P关于AB、AC的对称点P1、P2,(不写作法,保留作图痕迹),试判断点P1,P2与点A是否在同一直线上,并说明理由.
参考答案
一.选择题
1.解:点P(﹣3,2)关于x轴的对称点的坐标是(﹣3,﹣2).
故选:A.
2.解:∵点P(2,b)和点Q(a,﹣3)关于x轴对称,
∴a=2,b=3,
则a+b的值是:5.
故选:D.
3.解:A(3,4)关于x轴对称的点A′(3,﹣4),将点A′向左平移6个单位,得到点B(﹣3,﹣4),
故选:D.
4.解:∵点P(﹣2018,2019)关于y轴的对称点为(2018,2019),
∴对称点一定在第一象限.
故选:A.
5.解:∵a﹣m=4,∴a﹣4=m,
又∵b+n=0(b≠0),
∴b=﹣n,
∴把点A向左平移4个单位长度后,与点B关于x轴对称.
故选:A.
6.解:
故选:A.
7.解:∵点A(1,2),B(﹣1,2),
∴点A与点B关于y轴对称,
故选:B.
8.解:作△ABC关于直线MN的轴对称图形正确的是B选项,
故选:B.
9.解:如图,最多能画出6个格点三角形与△ABC成轴对称.
故选:A.
10.解:∵点C的坐标是(﹣1,1),作△ABC关于x轴对称的△A1B1C1,
∴点C的对应点C1的坐标为:(﹣1,﹣1).
故选:D.
二.填空题
11.解:点P(1,2)关于y轴的对称点Q的坐标是:(﹣1,2).
故答案为:(﹣1,2).
12.解:∵点A(a,4)、点B(3,b)关于x轴对称,
∴a=3,b=﹣4,
∴a+b=﹣1,
故答案为:﹣1.
13.解:∵点P(4,2),
∴点P到直线x=1的距离为4﹣1=3,∴点P关于直线x=1的对称点P′到直线x=1的距离为3,
∴点P′的横坐标为1﹣3=﹣2,
∴对称点P′的坐标为(﹣2,2).
故答案为:(﹣2,2).
14.解:∵点A的坐标是(1,﹣2),
∴点A关于y轴的对称点A′(﹣1,﹣2),
∵将点A′先向上平移3个单位长度,而后向左平移2个单位长度,得到点A″,
∴点A″的坐标是(﹣1﹣2,﹣2+3),
即(﹣3,1),
故答案为:(﹣3,1).
15.解:∵点A(x,1)与点B(2,y)关于y轴对称,
∴x=﹣2,y=1,
故(x+y)2018=(﹣2+1)2018=1.
故答案为:1.
16.解:如图,过点C作CD⊥OB于D,
∵∠OCB=90°,OC=BC,
∴△BOC是等腰直角三角形,
∴CD=OD=OB,
∵O(0,0),B(﹣6,0),
∴OB=6,
∴CD=OD=×6=3,
∴点C的坐标为(﹣3,3),
∴点C关于y轴对称点C′的坐标是(3,3).
故答案为:(3,3).
17.解:∵A(﹣3,0),B(5,4),点P是线段AB的中点,
∴P(,),即P(1,2),
又∵P与Q关于x轴对称,
∴Q点坐标是(1,﹣2),
故答案为:(1,﹣2).
18.解:∵点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,
∴点M在第四象限,
∴,
解得:m<.
故答案为:m<.
三.解答题
19.解:由题意,得
M在第四象限,得
m﹣1>0,1﹣2m<0,
解得m>1,
在数轴上表示如图.
20.解:(1)如图,点(2,2),(﹣2,3),(4,﹣1)关于直线x=1的对称点的坐标分别为(0,2),(4,3),(﹣2,﹣1);
(2)如图,点(2,2),(﹣2,3),(4,﹣1)关于直线x=﹣1的对称点的坐标分别为(﹣4,2),(0,3),(﹣6,﹣1);
(3)点(a,b)关于直线x=m的对称点的坐标为(2m﹣a,b).
21.解:(1)
(2)
22.解:(1)根据题意得点C的坐标为(3,﹣2);
故答案为:(3,﹣2);
(2)△ABC的面积:.
故答案为:15;
(3)点C关于x轴对称的点D的坐标是(3,2);
故答案为:(3,2);
(4)将点B沿着与x轴平行的方向向右平移3个单位得到点B′(﹣3+3,﹣2),即(0,﹣2),
A、B′两点之间的距离是:3﹣(﹣2)=5;
故答案为:5;
(5),
∴四边形ABCD的面积为:S△ABC+S△ACD=15+6=21.
故答案为:21
23.解:(1)由图观察可知B1(5,3),C1、(﹣5,3),D1(﹣5,﹣3),E1(0,﹣5);
(2)结合图形并观察以上五组点的坐标,你会发现:坐标平面内任意一点P(a,b)关于直线y=x的对称点P1的坐标为 (b,a).
故答案为(b,a).
(3)根据任意一点P(a,b)关于直线y=x的对称点P1的坐标为 (b,a)可知,
解得.
所以点(x,y)的坐标为(1,﹣1).
24.解:(1)如图所示,△A1B1C1即为所求.
(2)△ABC的面积为2×3﹣×1×3﹣×1×2﹣×1×2=.
25.解:(1)①∵P1,P2是点P关于AB、AC的对称点,
∴PD=P1D,PE=P2E,
∴∠EDP=2∠DPP1,∠DEP=2∠EPP2,
∵∠DPP1+∠DPE+∠EPP2+∠A=180° ①,
2∠DPP1+∠DPE+2∠EPP2=180° ②
②﹣①得:∠DPP1+∠EPP2=∠A,
∵∠A=52°,
∴∠DPP1+∠EPP2=52°,
∴∠DPE=180°﹣(∠PDE+∠DEF)
=180°﹣2(∠DPP1+∠EPP2)
=180°﹣104°=76°.
(2)由(1)可知:∠DPE=180°﹣2∠A.
(3)点P1,P2与点A在同一条直线上.
理由如下:连接AP,AP1,AP2.
根据轴对称的性质,可得∠4=∠1,∠3=∠2,
∵∠BAC=90°,
即∠1+∠2=90°,
∴∠3+∠4=90°,
∴∠1+∠2+∠3+∠4=180°,
即∠P1AP2=180°,
∴点P1,P2与点A在同一条直线上.
