1.8分数乘法的应用(1)课件(14张PPT)
文档属性
| 名称 | 1.8分数乘法的应用(1)课件(14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-24 14:36:53 | ||
图片预览




文档简介
(共14张PPT)
分数乘法的
应用(1)
人教版数学六年级上册 第一单元
复习导入
基础练习
拓展练习
课堂小结
数学阅读
探究新知
复习导入
用字母表示出乘法运算定律,并说一说具体的内容。
a×b=b×a
乘法交换律:两个因数相乘,交换因数的位置,积不变。
a×b×c=(a×b)×c=a×(b×c)
乘法结合律:三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。
(a+b)×c=a×c+b×c
或(a-b)×c=a×c-b×c
乘法分配律:两个数的和(或差)与一个数相乘,可以把两个加数(或被减数、减数)分别与这个数相乘,在把两个积相加(或相减),结果不变。
a×c+b×c =(a+b)×c
或a×c-b×c=(a-b)×c
乘法分配律:一个数分别与两个数相乘的和或者差,可以用这个数乘两个数的和或者两个数的差,结果不变。
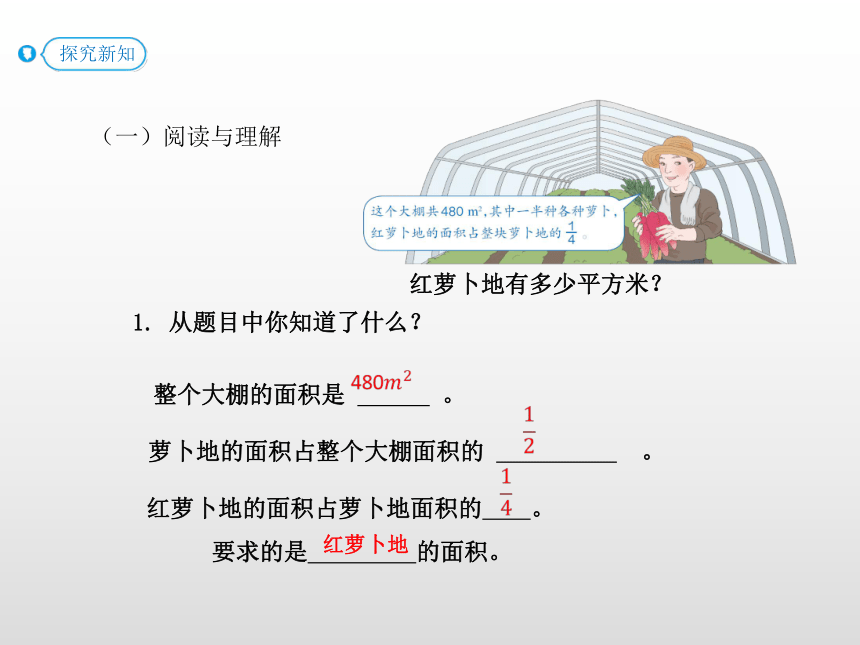
(一)阅读与理解
红萝卜地有多少平方米?
探究新知
1. 从题目中你知道了什么?
整个大棚的面积是 。
红萝卜地的面积占萝卜地面积的 。
要求的是 的面积。
红萝卜地
萝卜地的面积占整个大棚面积的 。
(一)阅读与理解
2. 怎样理解“其中的一半种各种萝卜”?
红萝卜地有多少平方米?
3. 怎样理解“红萝卜地的面积占整块萝卜地的 ”?
4
1
4. 要算红萝卜地的面积先要算出什么?
探究新知
(把这块地平均分成2份,其中1份种各种萝卜)
(把种各种萝卜的面积平均分成4份,红萝卜占其中的1份。)
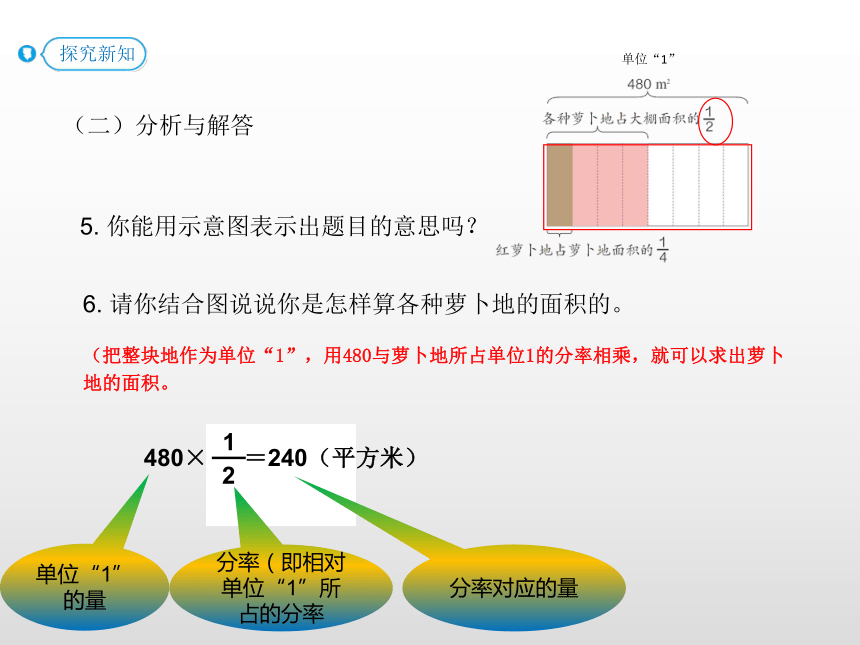
(二)分析与解答
5. 你能用示意图表示出题目的意思吗?
6. 请你结合图说说你是怎样算各种萝卜地的面积的。
2
1
480× =240(平方米)
探究新知
(把整块地作为单位“1”,用480与萝卜地所占单位1的分率相乘,就可以求出萝卜地的面积。
单位“1”
单位“1”的量
分率(即相对单位“1”所占的分率
分率对应的量
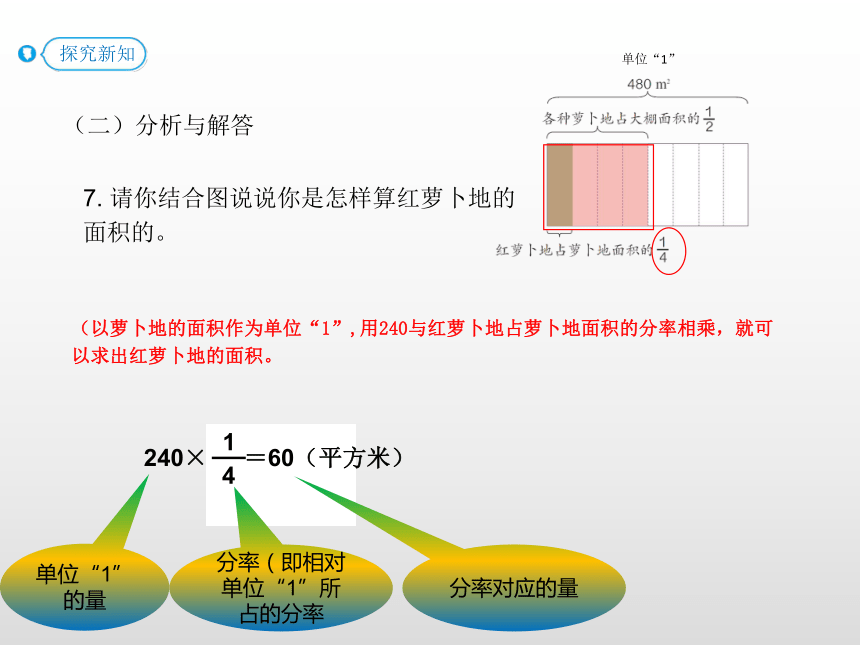
(二)分析与解答
7. 请你结合图说说你是怎样算红萝卜地的面积的。
4
1
240× =60(平方米)
探究新知
(以萝卜地的面积作为单位“1”,用240与红萝卜地占萝卜地面积的分率相乘,就可以求出红萝卜地的面积。
单位“1”
单位“1”的量
分率(即相对单位“1”所占的分率
分率对应的量
(二)分析与解答
2
1
480× =240(平方米)
4
1
240× =60(平方米)
×
4
1
2
1
=
8
1
8
1
480× =60(平方米)
探究新知
8.上面我们是分步计算的方法,先算出各种萝卜地的面积,再算出红萝卜地的面积。你有没有其他的方法呢?说说你的想法。
9.你能列出一个综合算式吗?
2
1
4
1
480 × ×
探究新知
10.你能计算出结果吗?
480
=
60
2
1
4
1
(
)
×
×
×
8
1
=
480
1
240
1
60
2
1
4
1
×
480
×
=60
(三)回顾与反思
研讨问题:请你结合图说说你检验的思路。
预设1:
60×4×2=480( )
探究新知
(红萝卜地的面积乘4表示萝卜地的面积,再乘2就是整个大棚的面积。)
预设2:
60×(4×2)=480( )
研讨问题:请你结合图说说你检验的思路。
(把整个大棚的面积平均分成2份,把其中的一份再平均分成4份,
相当于把整个大棚的面积平均分成了8份,红萝卜地占其中的1份是60 m ,
用1份的面积乘8就是整个大棚的面积。)
探究新知
1.求一个数的几分之几是多少,属于两个量相比的关系。用线段图可以比较清楚地表示出数量之间的关系:单位“1”的量×比较量占单位“1”的几分之几=比较量
2.解决连续求一个数的几分之几是多少的实际问题,弄清每一步单位“1”的量是谁最关键。
探究新知
4
3
想成为科学家的人数是想当老师人数的 。
3
1
想成为老师
36人
1、36 × × =9(人)
3
1
4
3
基础练习
?
这个班有多少名同学想成为科学家?
试着画出示意图,并列式计算。
先把全班当作单位“1”,算出想成为老师的人数,再把想当老师的人数当作单位“1”,算出想成为科学家的人数。
4
1
2、36 ×( × )=36×
3
1
4
3
=9(人)
先算出想成为科学家的人数占全班人数的几分之几。
拓展练习
答:这次考试女生及格了16人。
方法一:
方法二:
全班有学生40名,期中考试及格了其中及格的男生占了,请问这次考试女生一共及格了多少人?
有一个老太婆卖鸡蛋,第一个人买去老太婆一半鸡蛋,老太婆送给他半个鸡蛋;第二个人买去老太婆剩余的一半鸡蛋,老太婆又送给他半个鸡蛋;第三个人又买去剩下的一半, 老太婆又送给他半个鸡蛋;第四个人还是买去剩下的一半,老太婆又送给他半个鸡蛋。这时候,老太婆的鸡蛋才卖光。请问老太婆一共有多少个鸡蛋?
这道题里面,单位1在不停的变化,同时又有半个鸡蛋掺和,如果用一般的方程去解, 既费时又麻烦,这里,我们向大家介绍一种倒解法,这道题就变得非常容易了。
所谓的倒解法,就是从最后的结果向前推理,最后得出答案。
老太婆最后一个动作是送给第四个人半个鸡蛋,她的鸡蛋才买光,那就是说,如果不送, 剩下的半个鸡蛋就应该是第四个买完以后的状态,因为第四个人买的是她的一半鸡蛋,既然买完后还剩下半个鸡蛋,说明第四个人买去的也是半个鸡蛋,所以,第四个人买之前,老太 婆手里应该有1个(半个+半个)鸡蛋;再接着分析:这1个鸡蛋是她送给第三个人半个鸡蛋后的情况,那么没有送之前就应该是1个半鸡蛋,第三个人同样也是买了老太婆手里的鸡蛋,既然还剩下一个半鸡蛋,说明第三个人也买去了一个半鸡蛋,那么在第三个人没买之前,老太婆手里应该有3个鸡蛋( + ),用同样的方法去分析,第二个人没买之前,老太婆手里应该就有7个鸡蛋,第一个人没买之前,老太婆手里应该有15个鸡蛋。
具体算法就是: + =l; (1+ ) X2=3; ( 3+ ) X2=7; (7+ ) X2=15。
你明白了吗?
倒解法巧解应用题
数学阅读
分数乘法的
应用(1)
人教版数学六年级上册 第一单元
复习导入
基础练习
拓展练习
课堂小结
数学阅读
探究新知
复习导入
用字母表示出乘法运算定律,并说一说具体的内容。
a×b=b×a
乘法交换律:两个因数相乘,交换因数的位置,积不变。
a×b×c=(a×b)×c=a×(b×c)
乘法结合律:三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。
(a+b)×c=a×c+b×c
或(a-b)×c=a×c-b×c
乘法分配律:两个数的和(或差)与一个数相乘,可以把两个加数(或被减数、减数)分别与这个数相乘,在把两个积相加(或相减),结果不变。
a×c+b×c =(a+b)×c
或a×c-b×c=(a-b)×c
乘法分配律:一个数分别与两个数相乘的和或者差,可以用这个数乘两个数的和或者两个数的差,结果不变。
(一)阅读与理解
红萝卜地有多少平方米?
探究新知
1. 从题目中你知道了什么?
整个大棚的面积是 。
红萝卜地的面积占萝卜地面积的 。
要求的是 的面积。
红萝卜地
萝卜地的面积占整个大棚面积的 。
(一)阅读与理解
2. 怎样理解“其中的一半种各种萝卜”?
红萝卜地有多少平方米?
3. 怎样理解“红萝卜地的面积占整块萝卜地的 ”?
4
1
4. 要算红萝卜地的面积先要算出什么?
探究新知
(把这块地平均分成2份,其中1份种各种萝卜)
(把种各种萝卜的面积平均分成4份,红萝卜占其中的1份。)
(二)分析与解答
5. 你能用示意图表示出题目的意思吗?
6. 请你结合图说说你是怎样算各种萝卜地的面积的。
2
1
480× =240(平方米)
探究新知
(把整块地作为单位“1”,用480与萝卜地所占单位1的分率相乘,就可以求出萝卜地的面积。
单位“1”
单位“1”的量
分率(即相对单位“1”所占的分率
分率对应的量
(二)分析与解答
7. 请你结合图说说你是怎样算红萝卜地的面积的。
4
1
240× =60(平方米)
探究新知
(以萝卜地的面积作为单位“1”,用240与红萝卜地占萝卜地面积的分率相乘,就可以求出红萝卜地的面积。
单位“1”
单位“1”的量
分率(即相对单位“1”所占的分率
分率对应的量
(二)分析与解答
2
1
480× =240(平方米)
4
1
240× =60(平方米)
×
4
1
2
1
=
8
1
8
1
480× =60(平方米)
探究新知
8.上面我们是分步计算的方法,先算出各种萝卜地的面积,再算出红萝卜地的面积。你有没有其他的方法呢?说说你的想法。
9.你能列出一个综合算式吗?
2
1
4
1
480 × ×
探究新知
10.你能计算出结果吗?
480
=
60
2
1
4
1
(
)
×
×
×
8
1
=
480
1
240
1
60
2
1
4
1
×
480
×
=60
(三)回顾与反思
研讨问题:请你结合图说说你检验的思路。
预设1:
60×4×2=480( )
探究新知
(红萝卜地的面积乘4表示萝卜地的面积,再乘2就是整个大棚的面积。)
预设2:
60×(4×2)=480( )
研讨问题:请你结合图说说你检验的思路。
(把整个大棚的面积平均分成2份,把其中的一份再平均分成4份,
相当于把整个大棚的面积平均分成了8份,红萝卜地占其中的1份是60 m ,
用1份的面积乘8就是整个大棚的面积。)
探究新知
1.求一个数的几分之几是多少,属于两个量相比的关系。用线段图可以比较清楚地表示出数量之间的关系:单位“1”的量×比较量占单位“1”的几分之几=比较量
2.解决连续求一个数的几分之几是多少的实际问题,弄清每一步单位“1”的量是谁最关键。
探究新知
4
3
想成为科学家的人数是想当老师人数的 。
3
1
想成为老师
36人
1、36 × × =9(人)
3
1
4
3
基础练习
?
这个班有多少名同学想成为科学家?
试着画出示意图,并列式计算。
先把全班当作单位“1”,算出想成为老师的人数,再把想当老师的人数当作单位“1”,算出想成为科学家的人数。
4
1
2、36 ×( × )=36×
3
1
4
3
=9(人)
先算出想成为科学家的人数占全班人数的几分之几。
拓展练习
答:这次考试女生及格了16人。
方法一:
方法二:
全班有学生40名,期中考试及格了其中及格的男生占了,请问这次考试女生一共及格了多少人?
有一个老太婆卖鸡蛋,第一个人买去老太婆一半鸡蛋,老太婆送给他半个鸡蛋;第二个人买去老太婆剩余的一半鸡蛋,老太婆又送给他半个鸡蛋;第三个人又买去剩下的一半, 老太婆又送给他半个鸡蛋;第四个人还是买去剩下的一半,老太婆又送给他半个鸡蛋。这时候,老太婆的鸡蛋才卖光。请问老太婆一共有多少个鸡蛋?
这道题里面,单位1在不停的变化,同时又有半个鸡蛋掺和,如果用一般的方程去解, 既费时又麻烦,这里,我们向大家介绍一种倒解法,这道题就变得非常容易了。
所谓的倒解法,就是从最后的结果向前推理,最后得出答案。
老太婆最后一个动作是送给第四个人半个鸡蛋,她的鸡蛋才买光,那就是说,如果不送, 剩下的半个鸡蛋就应该是第四个买完以后的状态,因为第四个人买的是她的一半鸡蛋,既然买完后还剩下半个鸡蛋,说明第四个人买去的也是半个鸡蛋,所以,第四个人买之前,老太 婆手里应该有1个(半个+半个)鸡蛋;再接着分析:这1个鸡蛋是她送给第三个人半个鸡蛋后的情况,那么没有送之前就应该是1个半鸡蛋,第三个人同样也是买了老太婆手里的鸡蛋,既然还剩下一个半鸡蛋,说明第三个人也买去了一个半鸡蛋,那么在第三个人没买之前,老太婆手里应该有3个鸡蛋( + ),用同样的方法去分析,第二个人没买之前,老太婆手里应该就有7个鸡蛋,第一个人没买之前,老太婆手里应该有15个鸡蛋。
具体算法就是: + =l; (1+ ) X2=3; ( 3+ ) X2=7; (7+ ) X2=15。
你明白了吗?
倒解法巧解应用题
数学阅读
