4.2 比的基本性质(教材50-5例1)课件(19张PPT)
文档属性
| 名称 | 4.2 比的基本性质(教材50-5例1)课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 395.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-24 14:32:20 | ||
图片预览






文档简介
课件19张PPT。比的基本性质和
化简比人教版数学六年级上册 第四单元看谁填得对。(独立完成,小组互查,组长汇报)1、3÷5写成比的形式,前项是( ),后项是( ),比值是( )。2、六年级共有男生26人,女生24人。女生与男生的比是( : );男生与女生的比是( : ) ;全班学生与男生的比是( : );女生与全班学生的比是( : )。 3、边长为3厘米的正方形,周长与边长的比是( : );面积与边长的比是( : )。 ?5、湖光小学全校男、女生人数的比是6:5,男生与全校人数的比是( : ),全校人数与女生的比是 ( : ).3526242426502424501239327611115问题:小明、小强和小丽谁折得快?先说说你的办法,再计算。 一、比的基本性质 小明、小强、小丽都喜欢折纸鹤。有一天,他们三人在争论谁每分钟折的纸鹤数量多?
小明说:“我折的纸鹤数量与时间(分)的比是6︰8。”
小强说:“我折的纸鹤数量与时间(分)的比是3︰4。”
小丽说:“我折的纸鹤数量与时间(分)的比是12︰16。”要比较谁快,就是比工作效率,上面都是工作数量与工作时间的比,因为比就表示两个数相除关系,工作数量与工作时间的比,就是工作数量÷工作时间,算出来的就是工作效率,所以我们只要求出这三个比的比值,进行比较,谁大谁就快。问题:小明、小强和小丽谁折得快?先说说你的办法,再计算。 一、比的基本性质 小明、小强、小丽都喜欢折纸鹤。有一天,他们三人在争论谁每分钟折的纸鹤数量多?
小明说:“我折的纸鹤数量与时间(分)的比是6︰8。”
小强说:“我折的纸鹤数量与时间(分)的比是3︰4。”
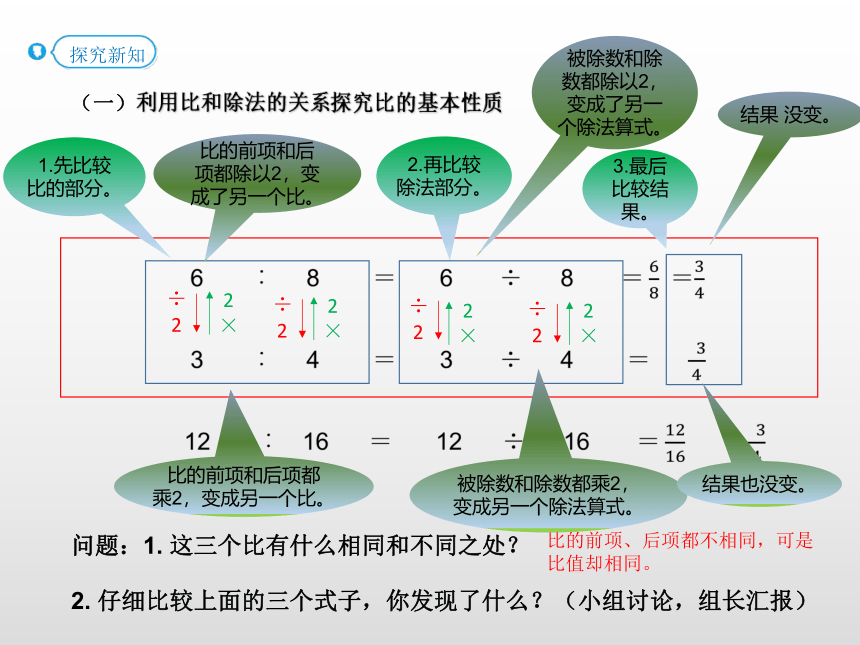
小丽说:“我折的纸鹤数量与时间(分)的比是12︰16。”问题:1. 这三个比有什么相同和不同之处?2. 仔细比较上面的三个式子,你发现了什么?(小组讨论,组长汇报)(一)利用比和除法的关系探究比的基本性质?比的前项、后项都不相同,可是比值却相同。1.先比较比的部分。2.再比较除法部分。比的前项和后项都除以2,变成了另一个比。被除数和除数都除以2,变成了另一个除法算式。3.最后比较结果。结果 没变。比的前项和后项都乘2,变成另一个比。被除数和除数都乘2,变成另一个除法算式。结果也没变。3. 你能总结出刚才的发现吗??比的前项和后项同时乘或除以相同的数,比值不变;被除数和除数同时乘或除以相同的数,商不变。(一)利用比和除法的关系探究比的基本性质4.试着把第1个比和第3个比,第2个和第3个比进行比较,看我们的发现对不对?(独立完成)5.试着给上面的几个比的前项和后项同时乘“0”,或者同时除以“0”,看我们的发现对不对?(一)利用比和除法的关系探究比的基本性质?比的前项和后项同时乘或除以相同的数(0除外),比值不变;被除数和除数同时乘或除以相同的数(0除外),商不变。6.那么我们对前面的发现,应该怎么说才正确?(一)利用比和除法的关系探究比的基本性质?比的前项和后项同时乘或除以相同的数(0除外),比值不变;7.刚才我们是根据比和除法的关系(两个数相除,我们也叫作这两个数的比,两个数的比表示这两数相除)进行了探索,发现了一个规律:被除数和除数同时乘或除以相同的数(0除外),商不变。事实上,被除数和除数同时乘或除以相同的数(0除外),商不变。 我们以前已经学过,所以不作为今天的发现,那么,我们今天的重要发现就是比的基本性质。
(一)利用比和除法的关系探究比的基本性质??1.比可以写成分数的形式,如下图。(二)利用比和分数的关系探究比的基本性质2.以小组为单位,自己按上面的方法,比较三个算式,说说你发现的规律。比的前项和后项同时乘或除以相同的数(0除外),比值不变;
分数的分子和分母同时乘或除以相同的数(0除外),分数的值不变。说一说你是怎样快速说出比值的?根据是什么?1. 根据108︰18=6,说出下面各比的比值。
54︰9 =( )
648︰108 =( )
10800︰1800=( )6662. 口算下面各比的比值。
818 48︰6 =( ) 4︰36 =( )
1800︰100 =( ) 0.06:0.54= ( )说一说你的方法。648÷54=12;108÷9=1210800÷54=200;1800÷9=200比的前后项同时除以它们的最大公约数。3. 判断并说明理由。
(1)6︰7=(6×0)︰(7×0)=0
(2)1︰2=(1+2)︰(2+2)=0.75
(3)2︰8=2︰(8÷2)=0.5问题:你觉得上面的做法正确吗?如果错误,错在哪里?×××上面的做法都不正确,没有按比的基本性质去做。1.根据我们以前所学的知识,谁能说一说“化简”是什么意思?像这样,比的前项和后项都是整数,且只有公因数1的比,叫作最简单的整数比。 18︰27 4︰9 3︰15
4.5︰9 5︰6 7︰11二、化简比(最简单的整数比的概念)我们以前学习分数时,化简就是将分数的分子和分母同时除以它们的最大公因数,使分数的分子和分母成为只有公因数1的互质数。2.看看下面各比,哪些比的前项和后项是互质的整数?上面其他比不是最简单的整数比,为什么?(小组讨论)例1:
“神舟”五号搭载了两面联合国旗,一面长15cm,宽10cm,另一面长180cm,宽120cm。这两面联合国旗的长和宽的最简单的整数比分别是多少? 1. 从信息中你知道了什么?要求什么?2. 自己尝试解决问题。反馈交流:5是15和10的什么数?为什么要除以5?60是180和120的什么数?为什么要除以60? 预设1:15︰10=(15÷5) ︰(10÷5)=3︰2
180︰120=(180÷60)︰(120÷60)= 3︰25是15和10的最大公约数,60是180和120的最大公约数。前后项同除以它们的最大公约数,就可以使前后项互质,成为最简单的整数比。1. 说一说你这样做的依据和方法?
2. 通过上面两个比的化简,你能说说化简整数比的方法吗?比可以写成分数的形式,然后可以按照化简分数的方法化简。化简整数比有两种方法:一种是根据比的基本性质,比的前项和后项同时除以它们的最大公因数;另一种是根据比和分数的关系,把比写成分数的形式,通过化简分数的方法,使它的前后项变为互质的整数。把下面各比化成最简单的整数比。0.75︰2=(0.75×100)︰(2×100)=75︰200=3︰845:30=(45÷15):30÷15 =3:2前项和后项同时扩大为原来的100倍,使小数比转化成整数比,再按照整数比的化简方法化简。前、后项同时乘它们分母的最小公倍数,先转化成整数比,再进行化简。前、后项同时除以它们的最大公因数。问题:自己尝试解决,反馈交流。把下面各比化成最简单的整数比。32︰16=2︰148︰40=6︰50.15︰0.3=1︰2=5︰1=14︰9=1︰5三、知识拓展,介绍黄金比问题:1. 你听说过“黄金比”吗?4. 你还了解生活中的黄金比吗?课下查阅相关的资料。 把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为 0.618︰1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。3. 找一找除了a︰b之外还有其他线段长度符合黄金比吗?2. 出示图片欣赏,介绍黄金比。 (c和a也符合黄金比)
化简比人教版数学六年级上册 第四单元看谁填得对。(独立完成,小组互查,组长汇报)1、3÷5写成比的形式,前项是( ),后项是( ),比值是( )。2、六年级共有男生26人,女生24人。女生与男生的比是( : );男生与女生的比是( : ) ;全班学生与男生的比是( : );女生与全班学生的比是( : )。 3、边长为3厘米的正方形,周长与边长的比是( : );面积与边长的比是( : )。 ?5、湖光小学全校男、女生人数的比是6:5,男生与全校人数的比是( : ),全校人数与女生的比是 ( : ).3526242426502424501239327611115问题:小明、小强和小丽谁折得快?先说说你的办法,再计算。 一、比的基本性质 小明、小强、小丽都喜欢折纸鹤。有一天,他们三人在争论谁每分钟折的纸鹤数量多?
小明说:“我折的纸鹤数量与时间(分)的比是6︰8。”
小强说:“我折的纸鹤数量与时间(分)的比是3︰4。”
小丽说:“我折的纸鹤数量与时间(分)的比是12︰16。”要比较谁快,就是比工作效率,上面都是工作数量与工作时间的比,因为比就表示两个数相除关系,工作数量与工作时间的比,就是工作数量÷工作时间,算出来的就是工作效率,所以我们只要求出这三个比的比值,进行比较,谁大谁就快。问题:小明、小强和小丽谁折得快?先说说你的办法,再计算。 一、比的基本性质 小明、小强、小丽都喜欢折纸鹤。有一天,他们三人在争论谁每分钟折的纸鹤数量多?
小明说:“我折的纸鹤数量与时间(分)的比是6︰8。”
小强说:“我折的纸鹤数量与时间(分)的比是3︰4。”
小丽说:“我折的纸鹤数量与时间(分)的比是12︰16。”问题:1. 这三个比有什么相同和不同之处?2. 仔细比较上面的三个式子,你发现了什么?(小组讨论,组长汇报)(一)利用比和除法的关系探究比的基本性质?比的前项、后项都不相同,可是比值却相同。1.先比较比的部分。2.再比较除法部分。比的前项和后项都除以2,变成了另一个比。被除数和除数都除以2,变成了另一个除法算式。3.最后比较结果。结果 没变。比的前项和后项都乘2,变成另一个比。被除数和除数都乘2,变成另一个除法算式。结果也没变。3. 你能总结出刚才的发现吗??比的前项和后项同时乘或除以相同的数,比值不变;被除数和除数同时乘或除以相同的数,商不变。(一)利用比和除法的关系探究比的基本性质4.试着把第1个比和第3个比,第2个和第3个比进行比较,看我们的发现对不对?(独立完成)5.试着给上面的几个比的前项和后项同时乘“0”,或者同时除以“0”,看我们的发现对不对?(一)利用比和除法的关系探究比的基本性质?比的前项和后项同时乘或除以相同的数(0除外),比值不变;被除数和除数同时乘或除以相同的数(0除外),商不变。6.那么我们对前面的发现,应该怎么说才正确?(一)利用比和除法的关系探究比的基本性质?比的前项和后项同时乘或除以相同的数(0除外),比值不变;7.刚才我们是根据比和除法的关系(两个数相除,我们也叫作这两个数的比,两个数的比表示这两数相除)进行了探索,发现了一个规律:被除数和除数同时乘或除以相同的数(0除外),商不变。事实上,被除数和除数同时乘或除以相同的数(0除外),商不变。 我们以前已经学过,所以不作为今天的发现,那么,我们今天的重要发现就是比的基本性质。
(一)利用比和除法的关系探究比的基本性质??1.比可以写成分数的形式,如下图。(二)利用比和分数的关系探究比的基本性质2.以小组为单位,自己按上面的方法,比较三个算式,说说你发现的规律。比的前项和后项同时乘或除以相同的数(0除外),比值不变;
分数的分子和分母同时乘或除以相同的数(0除外),分数的值不变。说一说你是怎样快速说出比值的?根据是什么?1. 根据108︰18=6,说出下面各比的比值。
54︰9 =( )
648︰108 =( )
10800︰1800=( )6662. 口算下面各比的比值。
818 48︰6 =( ) 4︰36 =( )
1800︰100 =( ) 0.06:0.54= ( )说一说你的方法。648÷54=12;108÷9=1210800÷54=200;1800÷9=200比的前后项同时除以它们的最大公约数。3. 判断并说明理由。
(1)6︰7=(6×0)︰(7×0)=0
(2)1︰2=(1+2)︰(2+2)=0.75
(3)2︰8=2︰(8÷2)=0.5问题:你觉得上面的做法正确吗?如果错误,错在哪里?×××上面的做法都不正确,没有按比的基本性质去做。1.根据我们以前所学的知识,谁能说一说“化简”是什么意思?像这样,比的前项和后项都是整数,且只有公因数1的比,叫作最简单的整数比。 18︰27 4︰9 3︰15
4.5︰9 5︰6 7︰11二、化简比(最简单的整数比的概念)我们以前学习分数时,化简就是将分数的分子和分母同时除以它们的最大公因数,使分数的分子和分母成为只有公因数1的互质数。2.看看下面各比,哪些比的前项和后项是互质的整数?上面其他比不是最简单的整数比,为什么?(小组讨论)例1:
“神舟”五号搭载了两面联合国旗,一面长15cm,宽10cm,另一面长180cm,宽120cm。这两面联合国旗的长和宽的最简单的整数比分别是多少? 1. 从信息中你知道了什么?要求什么?2. 自己尝试解决问题。反馈交流:5是15和10的什么数?为什么要除以5?60是180和120的什么数?为什么要除以60? 预设1:15︰10=(15÷5) ︰(10÷5)=3︰2
180︰120=(180÷60)︰(120÷60)= 3︰25是15和10的最大公约数,60是180和120的最大公约数。前后项同除以它们的最大公约数,就可以使前后项互质,成为最简单的整数比。1. 说一说你这样做的依据和方法?
2. 通过上面两个比的化简,你能说说化简整数比的方法吗?比可以写成分数的形式,然后可以按照化简分数的方法化简。化简整数比有两种方法:一种是根据比的基本性质,比的前项和后项同时除以它们的最大公因数;另一种是根据比和分数的关系,把比写成分数的形式,通过化简分数的方法,使它的前后项变为互质的整数。把下面各比化成最简单的整数比。0.75︰2=(0.75×100)︰(2×100)=75︰200=3︰845:30=(45÷15):30÷15 =3:2前项和后项同时扩大为原来的100倍,使小数比转化成整数比,再按照整数比的化简方法化简。前、后项同时乘它们分母的最小公倍数,先转化成整数比,再进行化简。前、后项同时除以它们的最大公因数。问题:自己尝试解决,反馈交流。把下面各比化成最简单的整数比。32︰16=2︰148︰40=6︰50.15︰0.3=1︰2=5︰1=14︰9=1︰5三、知识拓展,介绍黄金比问题:1. 你听说过“黄金比”吗?4. 你还了解生活中的黄金比吗?课下查阅相关的资料。 把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为 0.618︰1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。3. 找一找除了a︰b之外还有其他线段长度符合黄金比吗?2. 出示图片欣赏,介绍黄金比。 (c和a也符合黄金比)
