2.2.2 对数函数的基本内容 学案
文档属性
| 名称 | 2.2.2 对数函数的基本内容 学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-26 16:18:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
学案 对数函数的基本内容
知识要点
1.对数函数的概念
一般地,叫做对数函数,它的定义域是
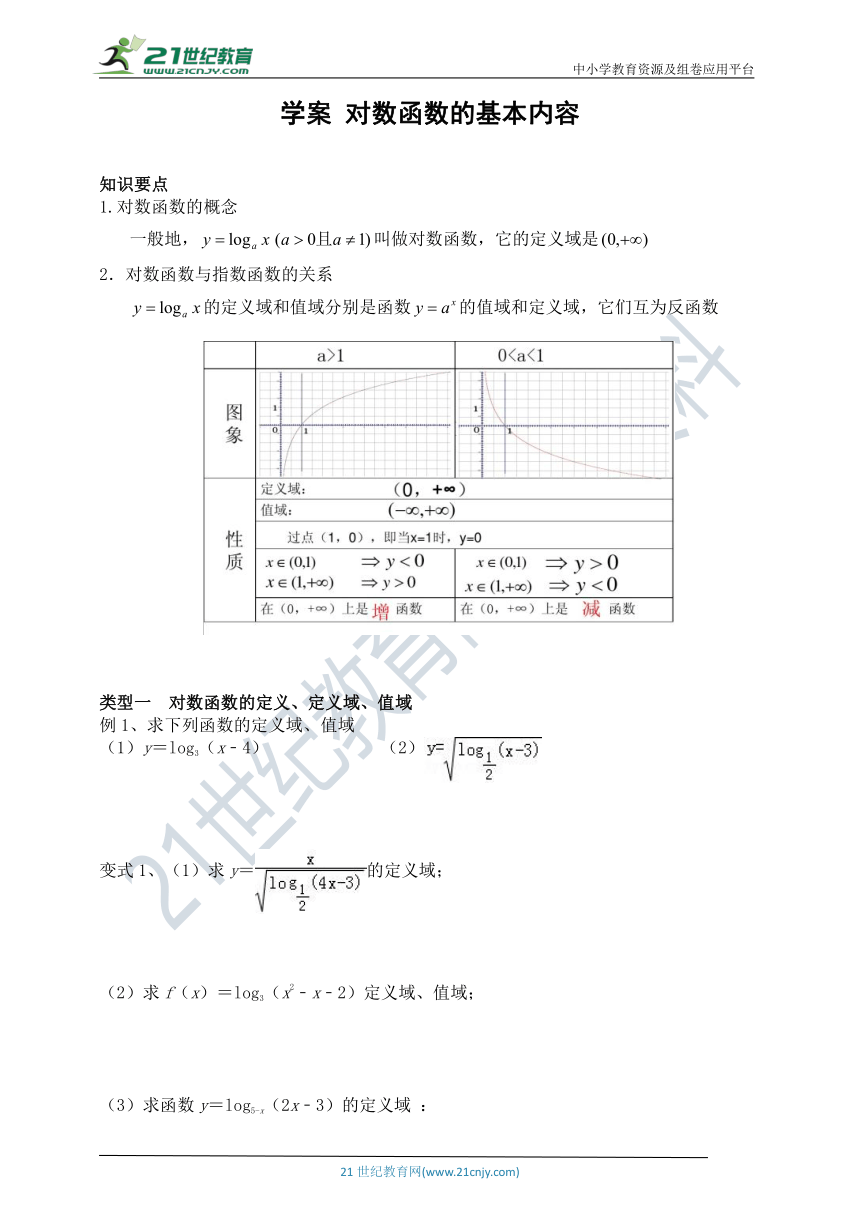
2.对数函数与指数函数的关系
的定义域和值域分别是函数的值域和定义域,它们互为反函数
类型一 对数函数的定义、定义域、值域
例1、求下列函数的定义域、值域
(1)y=log3(x﹣4) (2)
变式1、(1)求y=的定义域;
(2)求f(x)=log3(x2﹣x﹣2)定义域、值域;
求函数y=log5-x(2x﹣3)的定义域 :
(4)的定义域、值域
类型二 利用对数函数的性质,比较下列各组数中两个数的大小
例2、(1), (2), (3),
(4), (5),
变式2、若a=ln2,b=log23,c=log46,则a,b,c的大小关系是( )
类型三 定点问题
例3、函数y=loga(x+2)+3的图象恒过定点
变式3、已知函数y=loga(x﹣1)+2(a>0,a≠1)的图象恒过定点A,若点A也在函数f(x)=3x+b的图象上,则b= .
类型四 图像问题(x>1,底大图右)
例4、(1)函数y=logax,y=logbx,y=logcx,y=logdx的图象如图所示,则a,b,c,d大小顺序是( )
A.1<d<c<a<b B.c<d<1<a<b C.c<d<1<b<a D.d<c<1<a<b
(2) 函数y=﹣lg|x|的图象大致是( )
A. B.
C. D.
类型五 利用对数函数的性质,解不等式
(1)
(2)、若,则的取值范围是________
(3)、已知,,且,则的取值范围是________
答案
例1. 求下列函数的定义域
(1)解:因为x﹣4>0,得到x>4,故函数y=log2(x﹣4)的定义域为(4,+∞).值域R
(2)由函数可得,,故有0<x﹣3≤1,解得 3<x≤4,所以定义域为(3,4]。值域[0,+∞)
变式1.(1)由题意得:0<4x﹣3<1,解得:<x<1,
由题意得:x2﹣x﹣2>0,解得:x>2或x<﹣1,∴函数的定义域是:{x|x>2或x<﹣1}
值域R
由题意得:,解得:<x<5,且x≠4,所以定义域为∪(4,5)。
定义域(-∞,2),值域(-∞,4)
例2、(1)< (2)> (3)<
(4) (5)
变式2、解:,ln2<lne=1;
∴a<c<b.
例3.对于函数y=loga(x+2)+3,令x+2=1,可得x=﹣1,y=3,
故函数y=loga(x+2)+3的图象恒过定点(﹣1,3),故答案为:(﹣1,3).
变式3、解:令x﹣1=1,解得:x=2,此时y=2,故A(2,2),若点A(2,2)也在函数f(x)=3x+b的图象上,则9+b=2,解得:b=﹣7,故答案为:﹣7
例4、(1)解:令4个函数的函数值为1,即1=logax,1=logbx,1=logcx,1=logdx,
解得x1=a,x2=b,x3=c,x4=d;
作函数F(X)=1的图象从左到右依次与r(x),h(x),f(x),g(x)交于A(c,1)、B(d,1)、C(a,1)、D(b,1),所以,c<d<1<a<b.
(2)、解:∵f(﹣x)=﹣f(x)是偶函数,所以排除C,D,当x>0时,y=﹣lgx函数为减函数,排除A.故选:B.
例5.(1)(0,2)
(2)解:∵log(a+3)<1,∴log(a+3)<log(a+3)(a+3),
∴或,解得﹣3<a<﹣或a>﹣2.
∴a的取值范围是(﹣3,﹣)∪(﹣2,+∞).故答案为:(﹣3,﹣)∪(﹣2,+∞).
(3)解:∵0<a<1,0<b<1,如果<1,∴logb(x﹣3)>0,
∴0<x﹣3<1,∴3<x<4,故答案为:(3,4).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
