广西来宾市2018-2019学年八年级(下)期末数学试卷解析版
文档属性
| 名称 | 广西来宾市2018-2019学年八年级(下)期末数学试卷解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 300.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-23 17:36:29 | ||
图片预览



文档简介
广西来宾市2018-2019学年八年级(下)期末数学试卷
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有项符合题目要求.
1.(3分)若一个正多边形的外角等于45°,则这个多边形是( )
A.正八边形 B.正六边形 C.正五边形 D.正三角形
2.(3分)点P(1,﹣2)关于y轴对称的点的坐标是( )
A.(﹣1,﹣2) B.(1,2) C.(﹣1,2) D.(﹣2,1)
3.(3分)函数y=中自变量x的取值范围是( )
A.x≥3 B.x>3 C.x≤3 D.x<3
4.(3分)在下列以线段a、b、c的长为边,能构成直角三角形的是( )
A.a=3,b=4,c=6 B.a=5,b=6,c=7
C.a=6,b=8,c=9 D.a=7,b=24,c=25
5.(3分)在平面直角坐标系中,将点(1,2)先向左平移2个单位长度,再向下平移3个单位长度,则平移后得到的点是( )
A.(﹣1,﹣1) B.(﹣1,5) C.(3,﹣1) D.(3,5)
6.(3分)如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.∠BAC=∠BAD B.AC=AD或BC=BD
C.AC=AD且BC=BD D.以上都不正确
7.(3分)为了了解某校初三年级学生的运算能力,抽取了100名学生进行测试,将所得成绩(单位:分)整理后,列出下表:
分组 50~59 60~69 70~79 80~89 90~99
频率 0.06 0.16 0.08 0.30 0.40
本次测试这100名学生成绩良好(大于或等于80分为良好)的人数是( )
A.22 B.30 C.60 D.70
8.(3分)当b<0时,一次函数y=x+b的图象大致是( )
A. B.
C. D.
9.(3分)如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边落在对角线BD上,折痕为DG,点A落在点A1处,则A1G的长为( )
A.1 B. C. D.2
10.(3分)如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.7 B.10 C.11 D.12
11.(3分)如图,在矩形ABCD中,动点P从B点开始沿B→A→D→C的路径匀速运动到C点停止,在这个过程中,△PBC的面积S随时间t变化的图象大致是( )
A. B.
C. D.
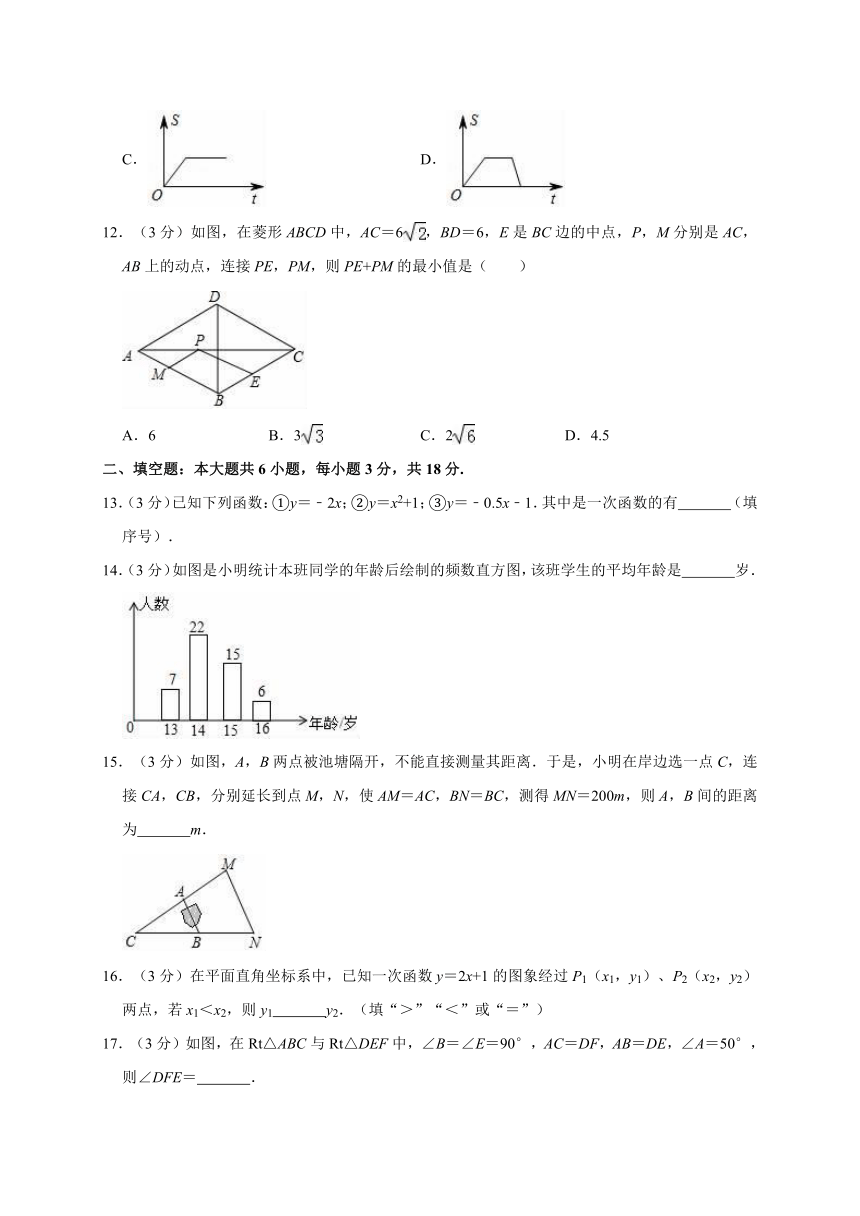
12.(3分)如图,在菱形ABCD中,AC=6,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
A.6 B.3 C.2 D.4.5
二、填空题:本大题共6小题,每小题3分,共18分.
13.(3分)已知下列函数:①y=﹣2x;②y=x2+1;③y=﹣0.5x﹣1.其中是一次函数的有 (填序号).
14.(3分)如图是小明统计本班同学的年龄后绘制的频数直方图,该班学生的平均年龄是 岁.
15.(3分)如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为 m.
16.(3分)在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 y2.(填“>”“<”或“=”)
17.(3分)如图,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,∠A=50°,则∠DFE= .
18.(3分)如图,将直角三角形纸片AOB置于平面直角坐标系中,已知点A(0,3),B(4,0),将直角三角形纸片绕其右下角的顶点依次按顺时针方向旋转,第一次旋转至图①位置,第二次旋转至图②位置,…,则直角三角形纸片旋转2019次后,其直角顶点与坐标轴原点的距离为 .
三、解答题:本大题共8小题,共66分.解答应写出文字说明、证明过程或演算步骤.
19.(6分)某地区为了增强市民的法制观念,随机抽取了一部分市民进行一次知识竞赛,将竞赛成绩(得分取整数)整理后分成五组并绘制成如图所示的频数直方图.请结合图中的信息,解答下列问题:
(1)抽取了多少人参加竞赛?
(2)60.5~70.5这一分数段的频数、频率分别是多少?
(3)这次竞赛成绩的中位数落在哪个分数段内?
20.(8分)△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某条直线对称?若是,请在图上画出这条对称轴.
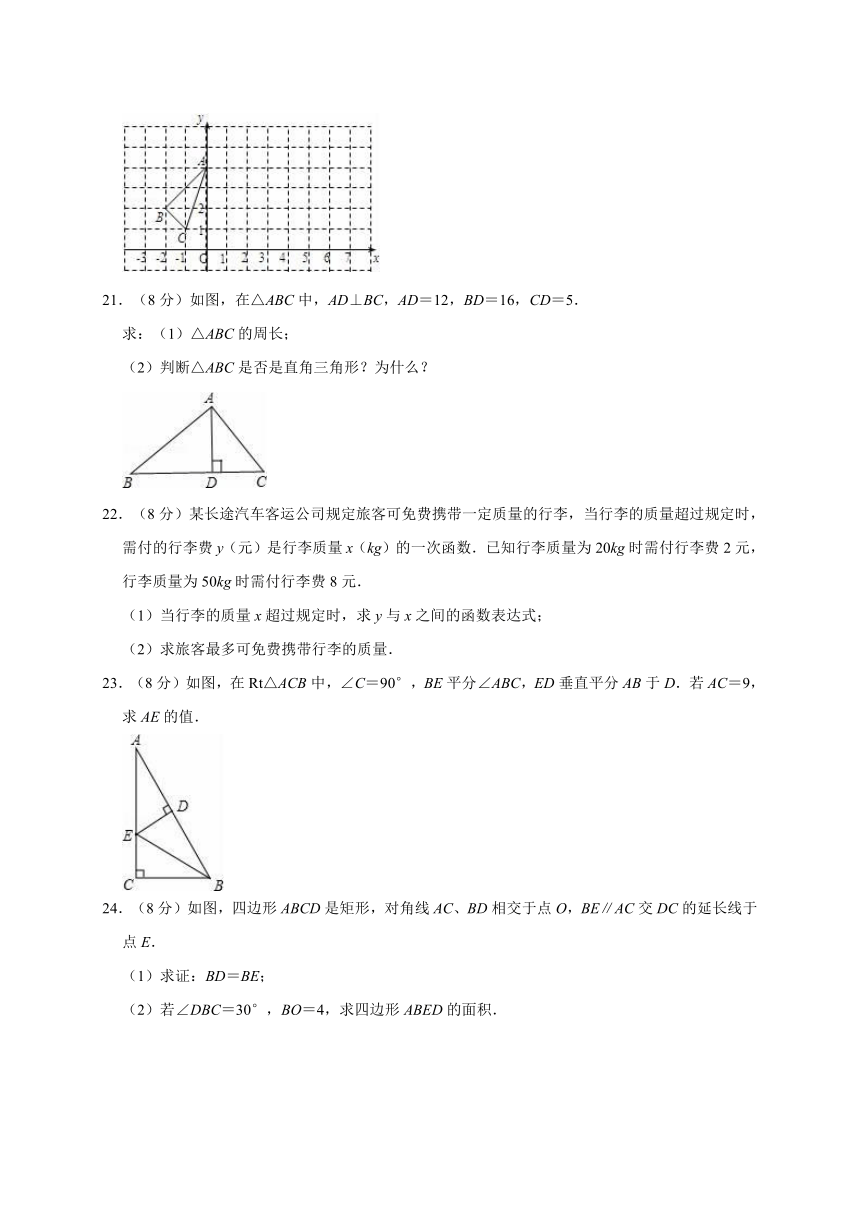
21.(8分)如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5.
求:(1)△ABC的周长;
(2)判断△ABC是否是直角三角形?为什么?
22.(8分)某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数.已知行李质量为20kg时需付行李费2元,行李质量为50kg时需付行李费8元.
(1)当行李的质量x超过规定时,求y与x之间的函数表达式;
(2)求旅客最多可免费携带行李的质量.
23.(8分)如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D.若AC=9,求AE的值.
24.(8分)如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
25.(10分)为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉,经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)直接写出当0≤x≤300和x>300时,y与x的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共1200m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?
26.(10分)在?ABCD中,对角线AC、BD交于点O,将过点A的直线l绕点A旋转,交射线CD于点E,BF⊥l于点F,DG⊥l于点G,连接OF,OG.
(1)如图①当点E与点C重合时,请直接写出线段OF,OG的数量关系;
(2)如图②,当点E在线段CD上时,OF与OG有什么数量关系?请证明你的结论;
(3)如图③,当点E在线段CD的延长线上时,上述的结论是否仍成立?请说明理由.
参考答案
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有项符合题目要求.
1.解:360÷45=8,即这个多边形的边数是8,
故选:A.
2.解:∵点P(1,﹣2)关于y轴对称,
∴点P(1,﹣2)关于y轴对称的点的坐标是(﹣1,﹣2).
故选:A.
3.解:由题意得3﹣x≥0,
解得x≤3.
故选:C.
4.解:A、32+42≠62,故不符合勾股定理的逆定理,不能组成直角三角形,故错误;
B、52+62≠72,故不符合勾股定理的逆定理,不能组成直角三角形,故错误;
C、62+82≠92,故不符合勾股定理的逆定理,不能组成直角三角形,故错误;
D、72+242=252,故符合勾股定理的逆定理,能组成直角三角形,故正确.
故选:D.
5.解:将点(1,2)先向左平移2个单位长度,再向下平移3个单位长度,
则平移后得到的点是(1﹣2,2﹣3),即(﹣1,﹣1),
故选:A.
6.解:从图中可知AB为Rt△ABC和Rt△ABD的斜边,也是公共边.
很据“HL”定理,证明Rt△ABC≌Rt△ABD,
还需补充一对直角边相等,
即AC=AD或BC=BD,
故选:B.
7.解:100×(0.30+0.40)=70.
故本次测试这100名学生成绩良好(大于或等于80分为良好)的人数是70人.
故选:D.
8.解:∵k=1>0,b<0,
∴一次函数y=x+b的图象经过第一、三、四象限.
故选:B.
9.解:设AG=x,
∵四边形ABCD是矩形,
∴∠A=90°,
∵AB=4,AD=3,
∴BD==5,
由折叠的性质可得:A1D=AD=3,A1G=AG=x,∠DA1G=∠A=90°,
∴∠BA1G=90°,BG=AB﹣AG=4﹣x,A1B=BD﹣A1D=5﹣3=2,
∵在Rt△A1BG中,A1G2+A1B2=BG2,
∴x2+22=(4﹣x)2,
解得:x=,
∴A1G=AG=.
故选:C.
10.解:∵AC的垂直平分线交AD于E,
∴AE=EC,
∵四边形ABCD是平行四边形,
∴DC=AB=4,AD=BC=6,
∴△CDE的周长为:EC+CD+ED=AD+CD=6+4=10,
故选:B.
11.解:当点P在AB上,S=BC×PB,则随t的增大,S逐渐增大;
当点P在AD上,S=BC×AB,则S是定值;
当点P在CD上,S=BC×CP,则随t的增大,S逐渐减小;
故选:B.
12.解:如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P,
则点P、M即为使PE+PM取得最小值,
其PE+PM=PE′+PM=E′M,
∵四边形ABCD是菱形,
∴点E′在CD上,
∵AC=6,BD=6,
∴AB==3,
由S菱形ABCD=AC?BD=AB?E′M得×6×6=3?E′M,
解得:E′M=2,
即PE+PM的最小值是2,
故选:C.
二、填空题:本大题共6小题,每小题3分,共18分.
13.解:①y=﹣2x是一次函数;
②y=x2+1自变量次数不为1,故不是一次函数;
③y=﹣0.5x﹣1是一次函数.
故答案是:①③.
14.解:该班学生的平均年龄是=14.4(岁),
故答案为:14.4.
15.解:∵AM=AC,BN=BC,
∴AB是△CMN的中位线,
∴AB=MN=100m,
故答案为:100.
16.解:∵一次函数y=2x+1中k=2>0,
∴y随x的增大而增大,
∵x1<x2,
∴y1<y2.
故答案为:<.
17.解:在Rt△ABC与Rt△DEF中,
∵∠B=∠E=90°,AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(HL)
∴∠D=∠A=50°,
∴∠DFE=90°﹣∠D=90°﹣50°=40°.
故填40.
18.解:∵A(0,3),B(4,0),
∴OA=3,OB=4,
∵∠AOB=90°,
∴AB=,
5+3+4=12,
∵三次一个循环,2019÷3=673,
∴直角三角形纸片旋转2019次后,直角顶点在x轴上,
到原点的距离=673×12=8076,
故答案为8076.
三、解答题:本大题共8小题,共66分.解答应写出文字说明、证明过程或演算步骤.
19.解:(1)3+12+18+9+6=48(人),
答:抽取了48人参加竞赛;
(2)由统计图可知60.5~70.5这一分数段的频数为12,频率=0.25,
答:60.5~70.5这一分数段的频数、频率分别是12,0.,25;
(3)因为共有48名学生,所以中位数为第24、25名学生的中位数,即这次竞赛成绩的中位数落在70.5﹣80.5分数段内.
20.解:(1)由图知,A(0,4),B(﹣2,2),C(﹣1,1),
∴点A、B、C关于y轴对称的对称点为A1(0,4)、B1(2,2)、C1(1,1),
连接A1B1,A1C1,B1C1,得△A1B1C1;
(2)∵△ABC向右平移6个单位,
∴A、B、C三点的横坐标加6,纵坐标不变,
作出△A2B2C2,A2(6,4),B2(4,2),C2(5,1);
(3)△A1B1C1和△A2B2C2是轴对称图形,对称轴为图中直线l:x=3.
21.解:(1)在Rt△ABD和Rt△ACD中,
根据勾股定理得:AB2=AD2+BD2,AC2=AD2+CD2,
又AD=12,BD=16,CD=5,
∴AB=20,AC=13,
△ABC的周长=AB+AC+BC=AB+AC+BD+DC=20+13+16+5=54.
(2)∵AB=20,AC=13,BC=21,
AB2+AC2≠BC2,
∴△ABC不是直角三角形.
22.解:(1)设y与x的函数表达式为y=kx+b.
将(20,2)、(50,8)代入y=kx+b中,
,解得:,
∴当行李的质量x超过规定时,y与x之间的函数表达式为y=x﹣2.
(2)当y=0时, x﹣2=0,
解得:x=10.
答:旅客最多可免费携带行李10kg.
23.解:设AE=x,则CE=9﹣x.
∵BE平分∠ABC
又∵CE⊥CB,ED⊥AB
∴DE=CE=9﹣x,
∵DE垂直平分AB,
∴AE=BE,
∴∠A=∠ABE=∠CBE.
∵在RT△ACB中,∠A+∠ABC=90°,
∴∠A=∠ABE=∠CBE=30°,
∴DE=AE,即9﹣x=x,
∴x=6.
答:AE长为6.
24.(1)证明:∵四边形ABCD是矩形,
∴AC=BD,AB∥CD,
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE;
(2)解:∵在矩形ABCD中,BO=4,
∴BD=2BO=2×4=8,
∵∠DBC=30°,
∴CD=BD=×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=4+4=8,
在Rt△BCD中,BC===4,
∴四边形ABED的面积=(4+8)×4=24.
25.解:(1)y=
(2)设甲种花卉种植为 am2,则乙种花卉种植(1200﹣a)m2.
∴,
∴200≤a≤800
当200≤a≤300时,W1=130a+100(1200﹣a)=30a+120000.
当a=200 时.Wmin=126000 元
当300<a≤800时,W2=80a+15000+100(1200﹣a)=135000﹣20a.
当a=800时,Wmin=119000 元
∵119000<126000
∴当a=800时,总费用最少,最少总费用为119000元.
此时乙种花卉种植面积为1200﹣800=400m2.
答:应该分配甲、乙两种花卉的种植面积分别是800m2 和400m2,才能使种植总费用最少,最少总费用为119000元.
26.解:(1)OF=OG,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD,
∵BF⊥l于点F,DG⊥l于点G,
∴∠BFO=∠DGO=90°,
在△OBF和△ODG中,,
∴△OBF≌△ODG(AAS),
∴OF=OG;
(2)当点E在线段CD上时,OF=OG,理由如下:
延长GO交BF于点H,如图②所示:
∵BF⊥l于点F,DG⊥l于点G,
∴BF∥DG,
∴∠ODG=∠OBH,
在△ODG和△OBH中,,
∴△ODG≌△OBH(ASA),
∴OG=OH,
∵∠GFH=90°,
∴OF=GH=OG;
(3)当点E在线段CD的延长线上时,上述的结论仍成立,OF=OG;理由如下:
延长GO、FB交于点H,如图③所示:
∵四边形ABCD是平行四边形,
∴OB=OD,
∵BF⊥l于点F,DG⊥l于点G,
∴BF∥DG,
∴∠DGO=∠BHO,
在△ODG和△OBH中,,
∴△ODG≌△OBH(ASA),
∴OG=OH,
∵∠GFH=90°,
∴OF=GH=OG.
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有项符合题目要求.
1.(3分)若一个正多边形的外角等于45°,则这个多边形是( )
A.正八边形 B.正六边形 C.正五边形 D.正三角形
2.(3分)点P(1,﹣2)关于y轴对称的点的坐标是( )
A.(﹣1,﹣2) B.(1,2) C.(﹣1,2) D.(﹣2,1)
3.(3分)函数y=中自变量x的取值范围是( )
A.x≥3 B.x>3 C.x≤3 D.x<3
4.(3分)在下列以线段a、b、c的长为边,能构成直角三角形的是( )
A.a=3,b=4,c=6 B.a=5,b=6,c=7
C.a=6,b=8,c=9 D.a=7,b=24,c=25
5.(3分)在平面直角坐标系中,将点(1,2)先向左平移2个单位长度,再向下平移3个单位长度,则平移后得到的点是( )
A.(﹣1,﹣1) B.(﹣1,5) C.(3,﹣1) D.(3,5)
6.(3分)如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.∠BAC=∠BAD B.AC=AD或BC=BD
C.AC=AD且BC=BD D.以上都不正确
7.(3分)为了了解某校初三年级学生的运算能力,抽取了100名学生进行测试,将所得成绩(单位:分)整理后,列出下表:
分组 50~59 60~69 70~79 80~89 90~99
频率 0.06 0.16 0.08 0.30 0.40
本次测试这100名学生成绩良好(大于或等于80分为良好)的人数是( )
A.22 B.30 C.60 D.70
8.(3分)当b<0时,一次函数y=x+b的图象大致是( )
A. B.
C. D.
9.(3分)如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边落在对角线BD上,折痕为DG,点A落在点A1处,则A1G的长为( )
A.1 B. C. D.2
10.(3分)如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A.7 B.10 C.11 D.12
11.(3分)如图,在矩形ABCD中,动点P从B点开始沿B→A→D→C的路径匀速运动到C点停止,在这个过程中,△PBC的面积S随时间t变化的图象大致是( )
A. B.
C. D.
12.(3分)如图,在菱形ABCD中,AC=6,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
A.6 B.3 C.2 D.4.5
二、填空题:本大题共6小题,每小题3分,共18分.
13.(3分)已知下列函数:①y=﹣2x;②y=x2+1;③y=﹣0.5x﹣1.其中是一次函数的有 (填序号).
14.(3分)如图是小明统计本班同学的年龄后绘制的频数直方图,该班学生的平均年龄是 岁.
15.(3分)如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为 m.
16.(3分)在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 y2.(填“>”“<”或“=”)
17.(3分)如图,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,∠A=50°,则∠DFE= .
18.(3分)如图,将直角三角形纸片AOB置于平面直角坐标系中,已知点A(0,3),B(4,0),将直角三角形纸片绕其右下角的顶点依次按顺时针方向旋转,第一次旋转至图①位置,第二次旋转至图②位置,…,则直角三角形纸片旋转2019次后,其直角顶点与坐标轴原点的距离为 .
三、解答题:本大题共8小题,共66分.解答应写出文字说明、证明过程或演算步骤.
19.(6分)某地区为了增强市民的法制观念,随机抽取了一部分市民进行一次知识竞赛,将竞赛成绩(得分取整数)整理后分成五组并绘制成如图所示的频数直方图.请结合图中的信息,解答下列问题:
(1)抽取了多少人参加竞赛?
(2)60.5~70.5这一分数段的频数、频率分别是多少?
(3)这次竞赛成绩的中位数落在哪个分数段内?
20.(8分)△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某条直线对称?若是,请在图上画出这条对称轴.
21.(8分)如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5.
求:(1)△ABC的周长;
(2)判断△ABC是否是直角三角形?为什么?
22.(8分)某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数.已知行李质量为20kg时需付行李费2元,行李质量为50kg时需付行李费8元.
(1)当行李的质量x超过规定时,求y与x之间的函数表达式;
(2)求旅客最多可免费携带行李的质量.
23.(8分)如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D.若AC=9,求AE的值.
24.(8分)如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
25.(10分)为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉,经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)直接写出当0≤x≤300和x>300时,y与x的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共1200m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?
26.(10分)在?ABCD中,对角线AC、BD交于点O,将过点A的直线l绕点A旋转,交射线CD于点E,BF⊥l于点F,DG⊥l于点G,连接OF,OG.
(1)如图①当点E与点C重合时,请直接写出线段OF,OG的数量关系;
(2)如图②,当点E在线段CD上时,OF与OG有什么数量关系?请证明你的结论;
(3)如图③,当点E在线段CD的延长线上时,上述的结论是否仍成立?请说明理由.
参考答案
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有项符合题目要求.
1.解:360÷45=8,即这个多边形的边数是8,
故选:A.
2.解:∵点P(1,﹣2)关于y轴对称,
∴点P(1,﹣2)关于y轴对称的点的坐标是(﹣1,﹣2).
故选:A.
3.解:由题意得3﹣x≥0,
解得x≤3.
故选:C.
4.解:A、32+42≠62,故不符合勾股定理的逆定理,不能组成直角三角形,故错误;
B、52+62≠72,故不符合勾股定理的逆定理,不能组成直角三角形,故错误;
C、62+82≠92,故不符合勾股定理的逆定理,不能组成直角三角形,故错误;
D、72+242=252,故符合勾股定理的逆定理,能组成直角三角形,故正确.
故选:D.
5.解:将点(1,2)先向左平移2个单位长度,再向下平移3个单位长度,
则平移后得到的点是(1﹣2,2﹣3),即(﹣1,﹣1),
故选:A.
6.解:从图中可知AB为Rt△ABC和Rt△ABD的斜边,也是公共边.
很据“HL”定理,证明Rt△ABC≌Rt△ABD,
还需补充一对直角边相等,
即AC=AD或BC=BD,
故选:B.
7.解:100×(0.30+0.40)=70.
故本次测试这100名学生成绩良好(大于或等于80分为良好)的人数是70人.
故选:D.
8.解:∵k=1>0,b<0,
∴一次函数y=x+b的图象经过第一、三、四象限.
故选:B.
9.解:设AG=x,
∵四边形ABCD是矩形,
∴∠A=90°,
∵AB=4,AD=3,
∴BD==5,
由折叠的性质可得:A1D=AD=3,A1G=AG=x,∠DA1G=∠A=90°,
∴∠BA1G=90°,BG=AB﹣AG=4﹣x,A1B=BD﹣A1D=5﹣3=2,
∵在Rt△A1BG中,A1G2+A1B2=BG2,
∴x2+22=(4﹣x)2,
解得:x=,
∴A1G=AG=.
故选:C.
10.解:∵AC的垂直平分线交AD于E,
∴AE=EC,
∵四边形ABCD是平行四边形,
∴DC=AB=4,AD=BC=6,
∴△CDE的周长为:EC+CD+ED=AD+CD=6+4=10,
故选:B.
11.解:当点P在AB上,S=BC×PB,则随t的增大,S逐渐增大;
当点P在AD上,S=BC×AB,则S是定值;
当点P在CD上,S=BC×CP,则随t的增大,S逐渐减小;
故选:B.
12.解:如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P,
则点P、M即为使PE+PM取得最小值,
其PE+PM=PE′+PM=E′M,
∵四边形ABCD是菱形,
∴点E′在CD上,
∵AC=6,BD=6,
∴AB==3,
由S菱形ABCD=AC?BD=AB?E′M得×6×6=3?E′M,
解得:E′M=2,
即PE+PM的最小值是2,
故选:C.
二、填空题:本大题共6小题,每小题3分,共18分.
13.解:①y=﹣2x是一次函数;
②y=x2+1自变量次数不为1,故不是一次函数;
③y=﹣0.5x﹣1是一次函数.
故答案是:①③.
14.解:该班学生的平均年龄是=14.4(岁),
故答案为:14.4.
15.解:∵AM=AC,BN=BC,
∴AB是△CMN的中位线,
∴AB=MN=100m,
故答案为:100.
16.解:∵一次函数y=2x+1中k=2>0,
∴y随x的增大而增大,
∵x1<x2,
∴y1<y2.
故答案为:<.
17.解:在Rt△ABC与Rt△DEF中,
∵∠B=∠E=90°,AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(HL)
∴∠D=∠A=50°,
∴∠DFE=90°﹣∠D=90°﹣50°=40°.
故填40.
18.解:∵A(0,3),B(4,0),
∴OA=3,OB=4,
∵∠AOB=90°,
∴AB=,
5+3+4=12,
∵三次一个循环,2019÷3=673,
∴直角三角形纸片旋转2019次后,直角顶点在x轴上,
到原点的距离=673×12=8076,
故答案为8076.
三、解答题:本大题共8小题,共66分.解答应写出文字说明、证明过程或演算步骤.
19.解:(1)3+12+18+9+6=48(人),
答:抽取了48人参加竞赛;
(2)由统计图可知60.5~70.5这一分数段的频数为12,频率=0.25,
答:60.5~70.5这一分数段的频数、频率分别是12,0.,25;
(3)因为共有48名学生,所以中位数为第24、25名学生的中位数,即这次竞赛成绩的中位数落在70.5﹣80.5分数段内.
20.解:(1)由图知,A(0,4),B(﹣2,2),C(﹣1,1),
∴点A、B、C关于y轴对称的对称点为A1(0,4)、B1(2,2)、C1(1,1),
连接A1B1,A1C1,B1C1,得△A1B1C1;
(2)∵△ABC向右平移6个单位,
∴A、B、C三点的横坐标加6,纵坐标不变,
作出△A2B2C2,A2(6,4),B2(4,2),C2(5,1);
(3)△A1B1C1和△A2B2C2是轴对称图形,对称轴为图中直线l:x=3.
21.解:(1)在Rt△ABD和Rt△ACD中,
根据勾股定理得:AB2=AD2+BD2,AC2=AD2+CD2,
又AD=12,BD=16,CD=5,
∴AB=20,AC=13,
△ABC的周长=AB+AC+BC=AB+AC+BD+DC=20+13+16+5=54.
(2)∵AB=20,AC=13,BC=21,
AB2+AC2≠BC2,
∴△ABC不是直角三角形.
22.解:(1)设y与x的函数表达式为y=kx+b.
将(20,2)、(50,8)代入y=kx+b中,
,解得:,
∴当行李的质量x超过规定时,y与x之间的函数表达式为y=x﹣2.
(2)当y=0时, x﹣2=0,
解得:x=10.
答:旅客最多可免费携带行李10kg.
23.解:设AE=x,则CE=9﹣x.
∵BE平分∠ABC
又∵CE⊥CB,ED⊥AB
∴DE=CE=9﹣x,
∵DE垂直平分AB,
∴AE=BE,
∴∠A=∠ABE=∠CBE.
∵在RT△ACB中,∠A+∠ABC=90°,
∴∠A=∠ABE=∠CBE=30°,
∴DE=AE,即9﹣x=x,
∴x=6.
答:AE长为6.
24.(1)证明:∵四边形ABCD是矩形,
∴AC=BD,AB∥CD,
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE;
(2)解:∵在矩形ABCD中,BO=4,
∴BD=2BO=2×4=8,
∵∠DBC=30°,
∴CD=BD=×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=4+4=8,
在Rt△BCD中,BC===4,
∴四边形ABED的面积=(4+8)×4=24.
25.解:(1)y=
(2)设甲种花卉种植为 am2,则乙种花卉种植(1200﹣a)m2.
∴,
∴200≤a≤800
当200≤a≤300时,W1=130a+100(1200﹣a)=30a+120000.
当a=200 时.Wmin=126000 元
当300<a≤800时,W2=80a+15000+100(1200﹣a)=135000﹣20a.
当a=800时,Wmin=119000 元
∵119000<126000
∴当a=800时,总费用最少,最少总费用为119000元.
此时乙种花卉种植面积为1200﹣800=400m2.
答:应该分配甲、乙两种花卉的种植面积分别是800m2 和400m2,才能使种植总费用最少,最少总费用为119000元.
26.解:(1)OF=OG,理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD,
∵BF⊥l于点F,DG⊥l于点G,
∴∠BFO=∠DGO=90°,
在△OBF和△ODG中,,
∴△OBF≌△ODG(AAS),
∴OF=OG;
(2)当点E在线段CD上时,OF=OG,理由如下:
延长GO交BF于点H,如图②所示:
∵BF⊥l于点F,DG⊥l于点G,
∴BF∥DG,
∴∠ODG=∠OBH,
在△ODG和△OBH中,,
∴△ODG≌△OBH(ASA),
∴OG=OH,
∵∠GFH=90°,
∴OF=GH=OG;
(3)当点E在线段CD的延长线上时,上述的结论仍成立,OF=OG;理由如下:
延长GO、FB交于点H,如图③所示:
∵四边形ABCD是平行四边形,
∴OB=OD,
∵BF⊥l于点F,DG⊥l于点G,
∴BF∥DG,
∴∠DGO=∠BHO,
在△ODG和△OBH中,,
∴△ODG≌△OBH(ASA),
∴OG=OH,
∵∠GFH=90°,
∴OF=GH=OG.
同课章节目录
