人教版选修2-2 信息技术应用 曲边梯形的面积课件(52张)
文档属性
| 名称 | 人教版选修2-2 信息技术应用 曲边梯形的面积课件(52张) |

|
|
| 格式 | zip | ||
| 文件大小 | 561.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 00:00:00 | ||
图片预览





文档简介
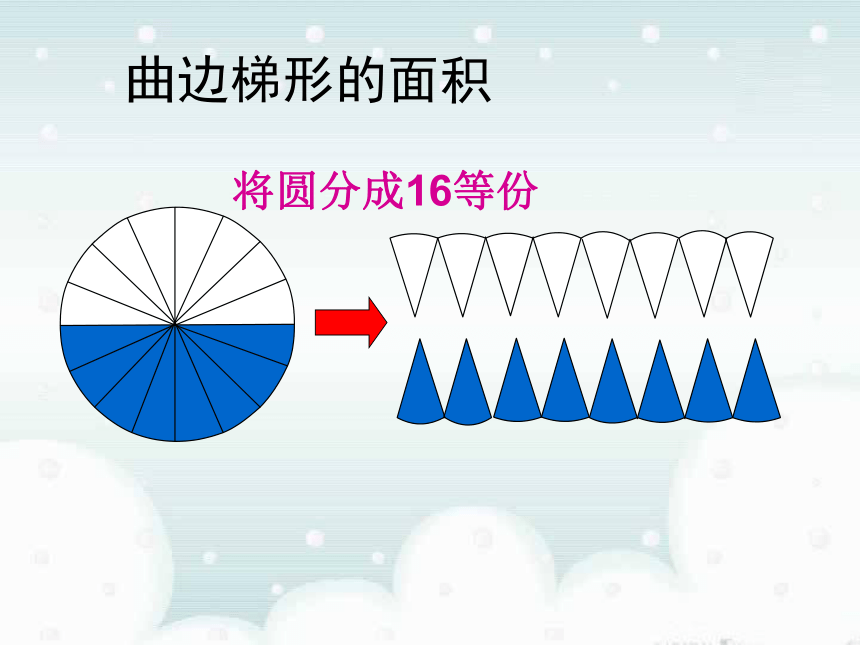
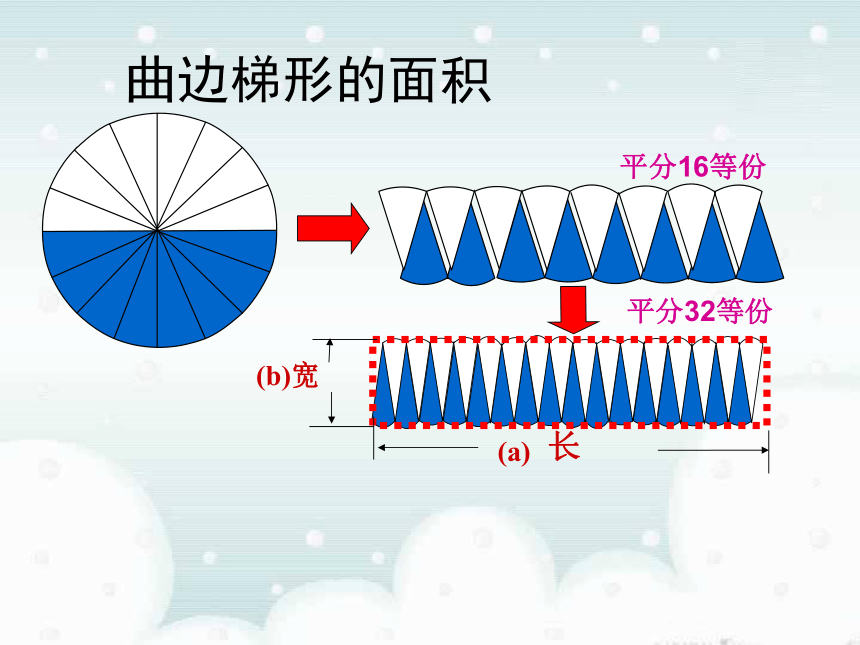
课件52张PPT。1.5.1 曲边梯形的面积 曲边梯形的面积问题2:圆面积公式是如何推导的?问题1最基本、最奇妙的曲边图形是什么? 曲边梯形的面积将圆分成16等份 曲边梯形的面积平分16等份平分32等份 曲边梯形的面积r因为: 长方形面积 = 长 × 宽
所以: 圆 的 面 积 =
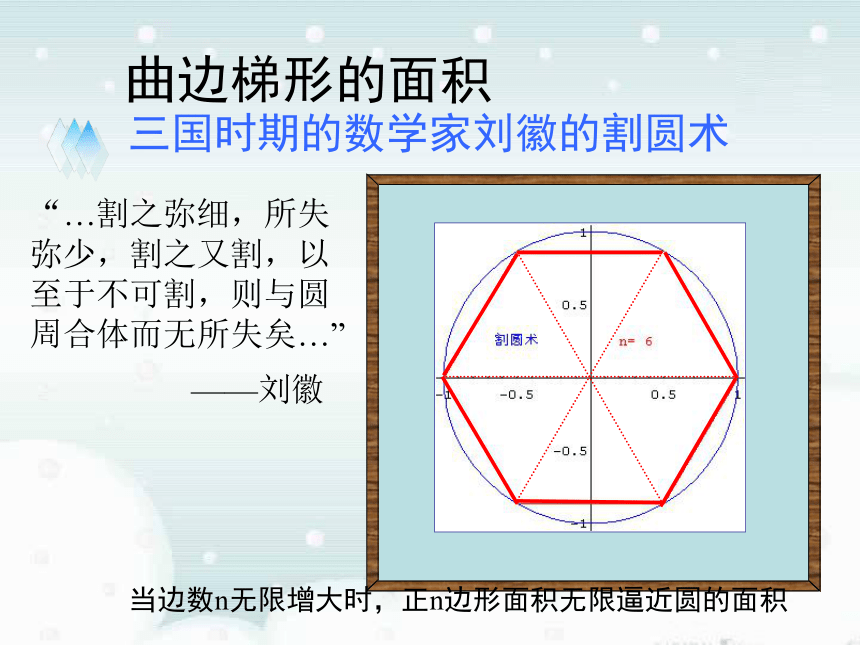
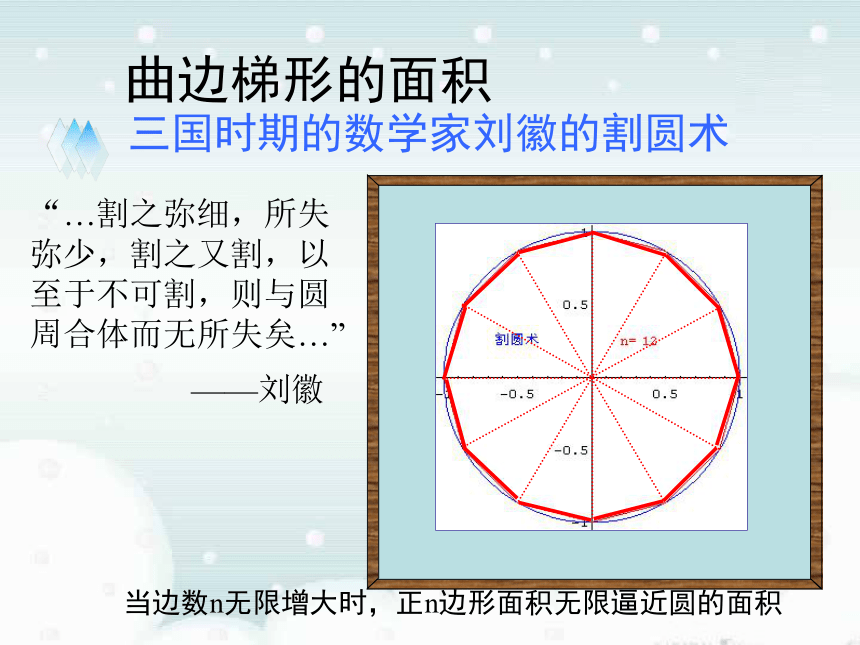
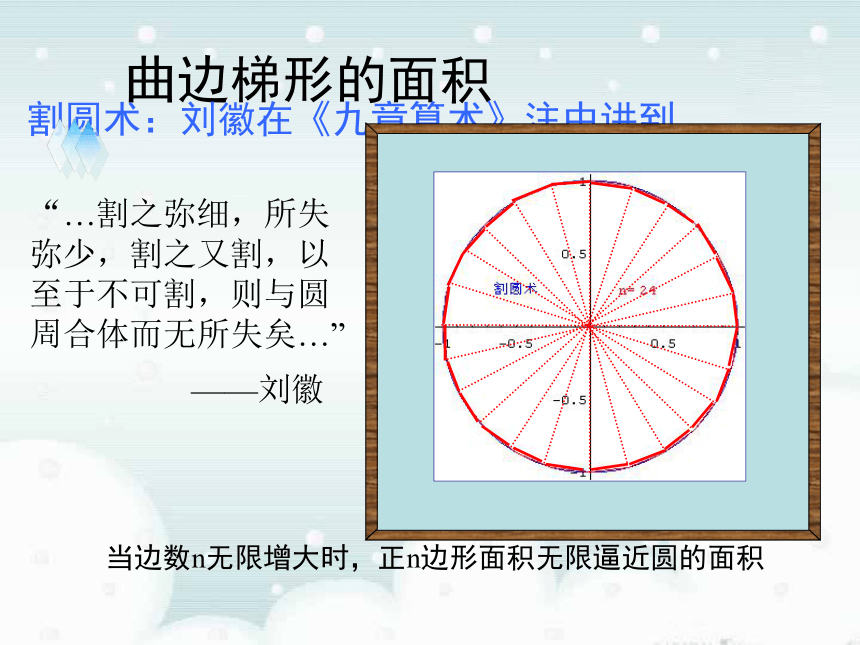
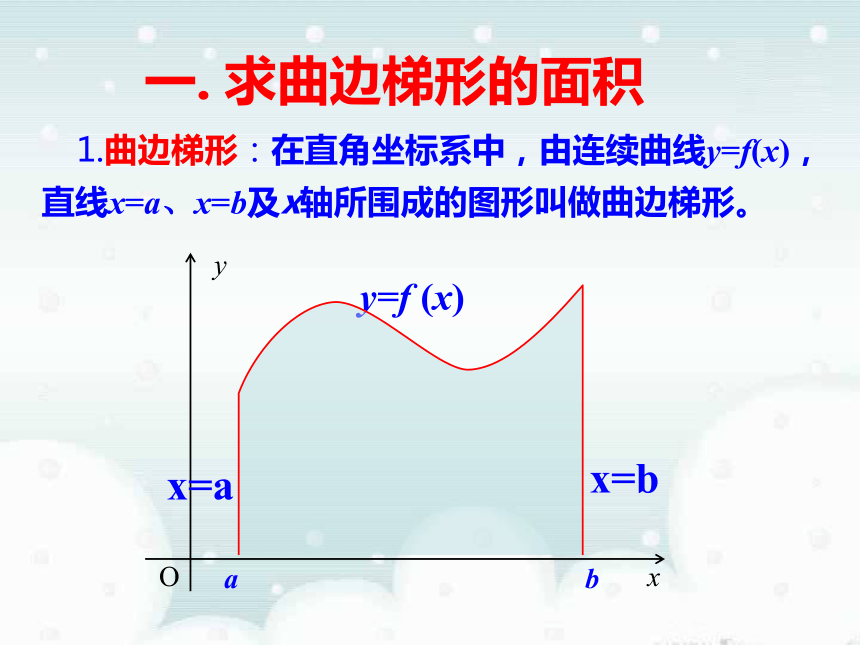
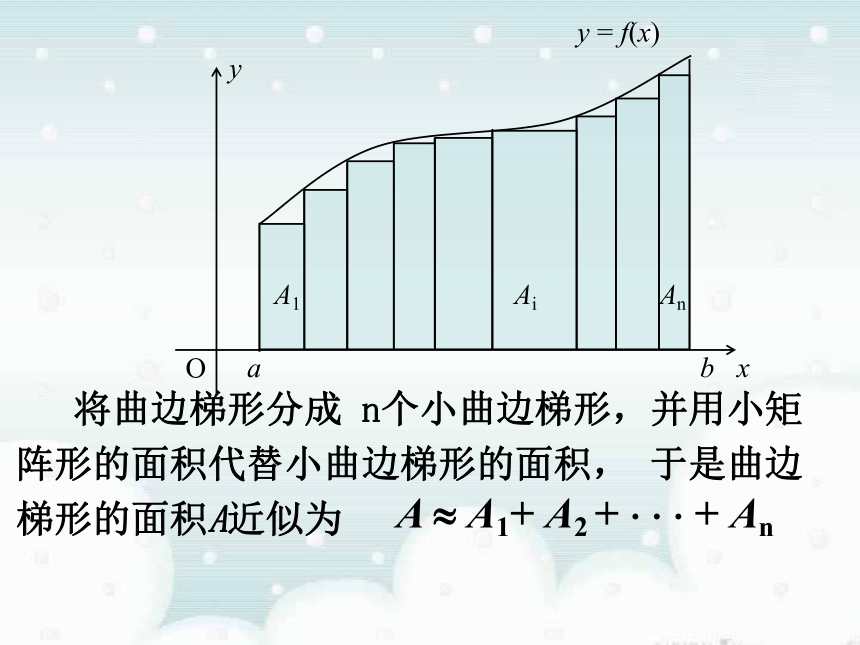
= πr 2πr × r 曲边梯形的面积三国时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽当边数n无限增大时,正n边形面积无限逼近圆的面积 曲边梯形的面积三国时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽当边数n无限增大时,正n边形面积无限逼近圆的面积 曲边梯形的面积“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”割圆术:刘徽在《九章算术》注中讲到——刘徽当边数n无限增大时,正n边形面积无限逼近圆的面积 1.曲边梯形:在直角坐标系中,由连续曲线y=f(x),直线x=a、x=b及x轴所围成的图形叫做曲边梯形。Ox y y=f (x)一. 求曲边梯形的面积x=ax=bA ? A1+ A2 + ? ? ? + An 将曲边梯形分成 n个小曲边梯形,并用小矩阵形的面积代替小曲边梯形的面积, 于是曲边梯形的面积A近似为 观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。(1)分割把区间[0,1]等分成n个小区间:过各区间端点作x轴的垂线,从而得到n个小曲边梯形,他们的面积分别记作例1.求抛物线y=x2、直线x=1和x轴所围成的
曲边梯形的面积。 (过剩近似值) (过剩近似值)1. 当n很大时,函数 在区间
上的值,可以用( )近似代替
A. B.
C. D.
C练 习C练 习求曲边梯形面积的“四步曲”:高中数学探究思考探究思考探究思考(2) 近似代替(3)求和(不足近似值)(4)取极限我们还可以
从数值上可
以看出这一
变化趋势
(请见表) 曲边梯形的面积4、逼近
所以: 圆 的 面 积 =
= πr 2πr × r 曲边梯形的面积三国时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽当边数n无限增大时,正n边形面积无限逼近圆的面积 曲边梯形的面积三国时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽当边数n无限增大时,正n边形面积无限逼近圆的面积 曲边梯形的面积“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”割圆术:刘徽在《九章算术》注中讲到——刘徽当边数n无限增大时,正n边形面积无限逼近圆的面积 1.曲边梯形:在直角坐标系中,由连续曲线y=f(x),直线x=a、x=b及x轴所围成的图形叫做曲边梯形。Ox y y=f (x)一. 求曲边梯形的面积x=ax=bA ? A1+ A2 + ? ? ? + An 将曲边梯形分成 n个小曲边梯形,并用小矩阵形的面积代替小曲边梯形的面积, 于是曲边梯形的面积A近似为 观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。观察以下演示,注意当分割加细时,
矩形面积和与曲边梯形面积的关系。(1)分割把区间[0,1]等分成n个小区间:过各区间端点作x轴的垂线,从而得到n个小曲边梯形,他们的面积分别记作例1.求抛物线y=x2、直线x=1和x轴所围成的
曲边梯形的面积。 (过剩近似值) (过剩近似值)1. 当n很大时,函数 在区间
上的值,可以用( )近似代替
A. B.
C. D.
C练 习C练 习求曲边梯形面积的“四步曲”:高中数学探究思考探究思考探究思考(2) 近似代替(3)求和(不足近似值)(4)取极限我们还可以
从数值上可
以看出这一
变化趋势
(请见表) 曲边梯形的面积4、逼近
