人教版选修2-1 习题3.2:1空间向量解决平行问题课件(20张)
文档属性
| 名称 | 人教版选修2-1 习题3.2:1空间向量解决平行问题课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 486.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 17:37:03 | ||
图片预览






文档简介
课件20张PPT。用空间向量解决立体几何中的平行问题研究 从今天开始,我们将进一步来体会向量这一工具在立体几何中的应用.1 空间向量的平行、垂直.
设a=(a1,a2,a3),b=(b1,b2,b3),
则a∥b?a=λb?____________________________ (λ∈R);
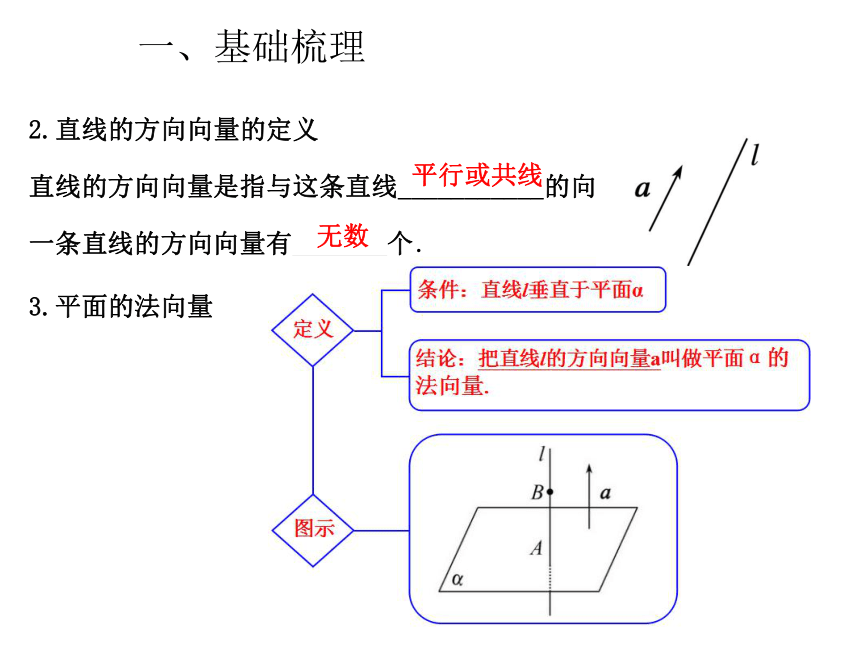
a⊥b?a·b=0?________________________;a1=λb1,a2=λb2,a3=λb3 a1b1+a2b2+a3b3=0一、基础梳理2.直线的方向向量的定义
直线的方向向量是指与这条直线___________的向量.
一条直线的方向向量有 个.
平行或共线一、基础梳理3.平面的法向量无数4.平面法向量的求法
(1)当已知平面的垂线时,在垂线上取一非零向量即可作为平面的法向量.
(2)当已知平面α内两不共线向量a=(a1,a2,a3),b=(b1,b2,b3)时,常用待定系数法求法向量:
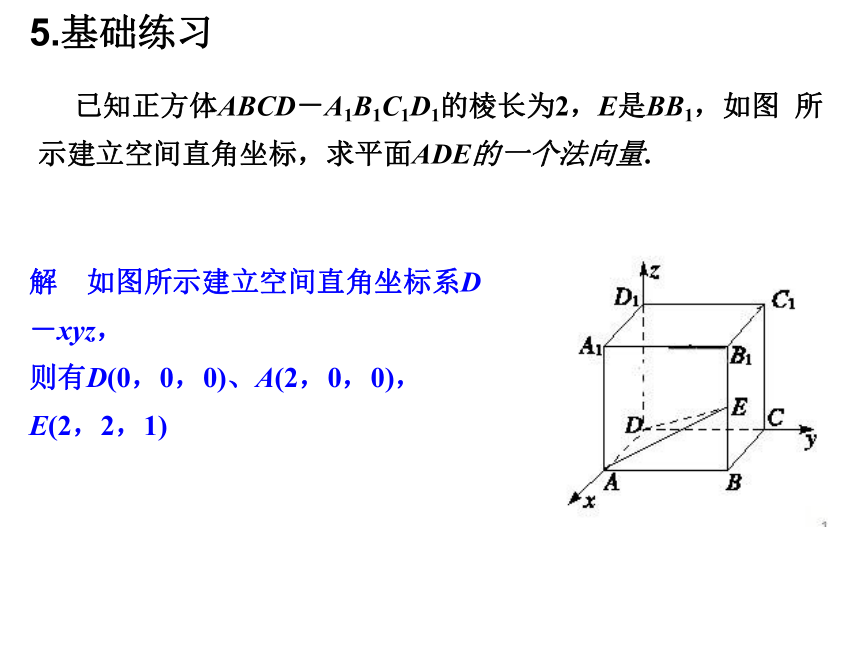
在上述方程组中,对x,y,z中的任一个赋值,求出另两个,所得n即为平面的法向量. 已知正方体ABCD-A1B1C1D1的棱长为2,E是BB1,如图 所示建立空间直角坐标,求平面ADE的一个法向量.
解 如图所示建立空间直角坐标系D-xyz,
则有D(0,0,0)、A(2,0,0),
E(2,2,1)5.基础练习由两个三元一次方程组成的方程组的解是不惟一的,为方便起见,取z=2。其实平面的法向量不是惟一的。
l1l2二、空间中平行关系的向量表示:
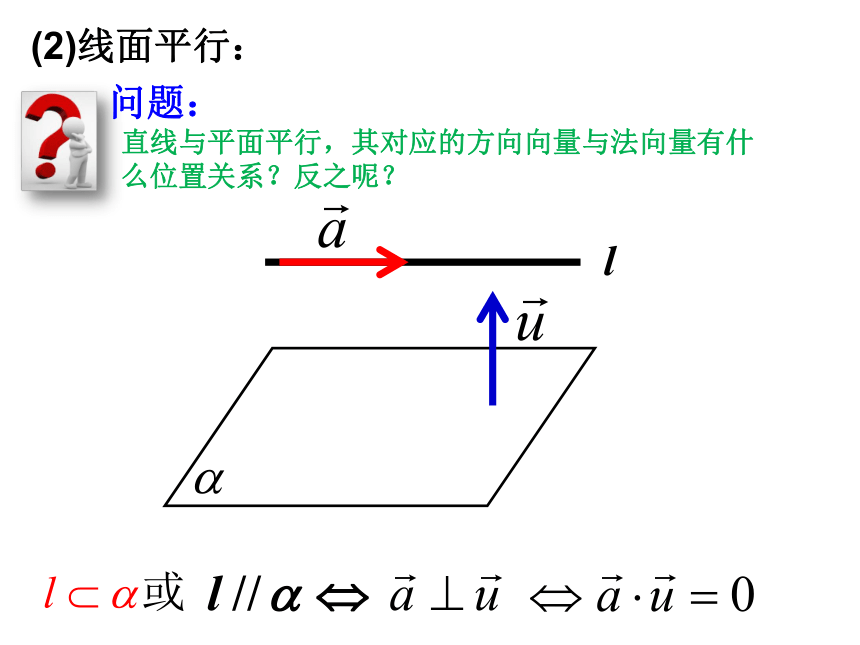
(1)线线平行: 两直线平行,其对应的方向向量有什么位置关系?反之呢?问题: l(2)线面平行:直线与平面平行,其对应的方向向量与法向量有什么位置关系?反之呢?问题: (3)面面平行:两平面平行,其对应的法向量有什么位置关系?反之呢?问题: 空间中平行关系总结(1)线线平行:
设直线l, m的方向向量分别为a=(x1, y1, z1), b=(x2, y2, z2),且x2, y2, z2≠0,则:
l //m . . . (2)线面平行:
设直线l的方向向量分别为a=(x1, y1, z1),平面α的法向量u=(x2, y2, z2),且x2, y2, z2≠0,则:
l // α . . . (3)面面平行:
设平面α,β的法向量分别为u=(x1, y1, z1), v=(x2, y2, z2),则:
α//β . . . a//ba⊥ua﹒u=0x1x2+y1y2+z1z2=0u//v题型一 利用方向向量和法向量判定线面位置关系
1。设a,b分别是不重合的直线l1,l2的方向向量,根据下列条件判断l1,l2的位置关系:
a=(4,6,-2),b=(-2,-3,1);
【例1】三、应用巩固2。设u是平面α的法向量,a是直线l的方向向量,根据下列条件判断平面α与l的位置关系;
u=(2,2,-1),a=(-6,8,4);
3。设u,v分别是不同的平面α,β的法向量,根据下列条件
判断α,β的位置关系;u=(3,0,0),v=(-2,0,0); (12分)已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是BB1、DD1的中点,求证:
(1)FC1∥平面ADE;
(2)平面ADE∥平面B1C1F.
题型二 利用空间向量证明平行问题【例2】证明 如图所示建立空间直角坐标系D-xyz,
则有D(0,0,0)、A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),B1(2,2,2),
(12分)已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是BB1、DD1的中点,求证:
(1)FC1∥平面ADE;
(2)平面ADE∥平面B1C1F.
【例2】在本题中除了运用空间向量的方法外还能用其它方法证明吗?传统证明方法(运用平行、垂直的判定和性质解决平行问题)运用空间向量的方法一定简单吗?问题: 可用【变式】 已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是AD、AB的中点,G是DD1 的四等分点,求证:
EG∥平面D1FC;
证明 如图所示建立空间直角坐标系D-xyz,
则有D(0,0,0)、A(2,0,0),C(0,2,0),D1(0,0,2),E(1,0,0),F(2,1,0),G(0,0,1/2),
能否快速运用传统方法解决问题?问题: 适用[思路分析]可先建系,写出直线的方向向量与平面的法向量,再用待定系数法确定点E.
解 分别以AB,AD,AP为x,y,z轴建立空间直角坐标系,
∴P(0,0,1),C(1,1,0),D(0,2,0),
四、课堂检测适用(1)线线平行的证明方法:
(2)线面平行的证明方法:(3)面面平行的证明方法:五、小结
设a=(a1,a2,a3),b=(b1,b2,b3),
则a∥b?a=λb?____________________________ (λ∈R);
a⊥b?a·b=0?________________________;a1=λb1,a2=λb2,a3=λb3 a1b1+a2b2+a3b3=0一、基础梳理2.直线的方向向量的定义
直线的方向向量是指与这条直线___________的向量.
一条直线的方向向量有 个.
平行或共线一、基础梳理3.平面的法向量无数4.平面法向量的求法
(1)当已知平面的垂线时,在垂线上取一非零向量即可作为平面的法向量.
(2)当已知平面α内两不共线向量a=(a1,a2,a3),b=(b1,b2,b3)时,常用待定系数法求法向量:
在上述方程组中,对x,y,z中的任一个赋值,求出另两个,所得n即为平面的法向量. 已知正方体ABCD-A1B1C1D1的棱长为2,E是BB1,如图 所示建立空间直角坐标,求平面ADE的一个法向量.
解 如图所示建立空间直角坐标系D-xyz,
则有D(0,0,0)、A(2,0,0),
E(2,2,1)5.基础练习由两个三元一次方程组成的方程组的解是不惟一的,为方便起见,取z=2。其实平面的法向量不是惟一的。
l1l2二、空间中平行关系的向量表示:
(1)线线平行: 两直线平行,其对应的方向向量有什么位置关系?反之呢?问题: l(2)线面平行:直线与平面平行,其对应的方向向量与法向量有什么位置关系?反之呢?问题: (3)面面平行:两平面平行,其对应的法向量有什么位置关系?反之呢?问题: 空间中平行关系总结(1)线线平行:
设直线l, m的方向向量分别为a=(x1, y1, z1), b=(x2, y2, z2),且x2, y2, z2≠0,则:
l //m . . . (2)线面平行:
设直线l的方向向量分别为a=(x1, y1, z1),平面α的法向量u=(x2, y2, z2),且x2, y2, z2≠0,则:
l // α . . . (3)面面平行:
设平面α,β的法向量分别为u=(x1, y1, z1), v=(x2, y2, z2),则:
α//β . . . a//ba⊥ua﹒u=0x1x2+y1y2+z1z2=0u//v题型一 利用方向向量和法向量判定线面位置关系
1。设a,b分别是不重合的直线l1,l2的方向向量,根据下列条件判断l1,l2的位置关系:
a=(4,6,-2),b=(-2,-3,1);
【例1】三、应用巩固2。设u是平面α的法向量,a是直线l的方向向量,根据下列条件判断平面α与l的位置关系;
u=(2,2,-1),a=(-6,8,4);
3。设u,v分别是不同的平面α,β的法向量,根据下列条件
判断α,β的位置关系;u=(3,0,0),v=(-2,0,0); (12分)已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是BB1、DD1的中点,求证:
(1)FC1∥平面ADE;
(2)平面ADE∥平面B1C1F.
题型二 利用空间向量证明平行问题【例2】证明 如图所示建立空间直角坐标系D-xyz,
则有D(0,0,0)、A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),B1(2,2,2),
(12分)已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是BB1、DD1的中点,求证:
(1)FC1∥平面ADE;
(2)平面ADE∥平面B1C1F.
【例2】在本题中除了运用空间向量的方法外还能用其它方法证明吗?传统证明方法(运用平行、垂直的判定和性质解决平行问题)运用空间向量的方法一定简单吗?问题: 可用【变式】 已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是AD、AB的中点,G是DD1 的四等分点,求证:
EG∥平面D1FC;
证明 如图所示建立空间直角坐标系D-xyz,
则有D(0,0,0)、A(2,0,0),C(0,2,0),D1(0,0,2),E(1,0,0),F(2,1,0),G(0,0,1/2),
能否快速运用传统方法解决问题?问题: 适用[思路分析]可先建系,写出直线的方向向量与平面的法向量,再用待定系数法确定点E.
解 分别以AB,AD,AP为x,y,z轴建立空间直角坐标系,
∴P(0,0,1),C(1,1,0),D(0,2,0),
四、课堂检测适用(1)线线平行的证明方法:
(2)线面平行的证明方法:(3)面面平行的证明方法:五、小结
