人教版选修2-1 3.1.4 空间向量的正交分解及其坐标表示课件(18张)
文档属性
| 名称 | 人教版选修2-1 3.1.4 空间向量的正交分解及其坐标表示课件(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 999.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 17:38:28 | ||
图片预览





文档简介
课件18张PPT。3.1.4《空间向量运算的
正交分解及基坐标表示》教学目标⒈理解空间向量的基底、基向量的概念.理解空间任一向量可用空间不共面的三个已知向量唯一线性表出;
⒉理解共面向量定理及其推论;掌握点在已知平面内的充要条件;
⒊会用上述知识解决立体几何中有关的简单问题.
教学重点:点在已知平面内的充要条件.共线、共面定理及其应用.
教学难点:对点在已知平面内的充要条件的理解与运用.
授课类型:新授课.
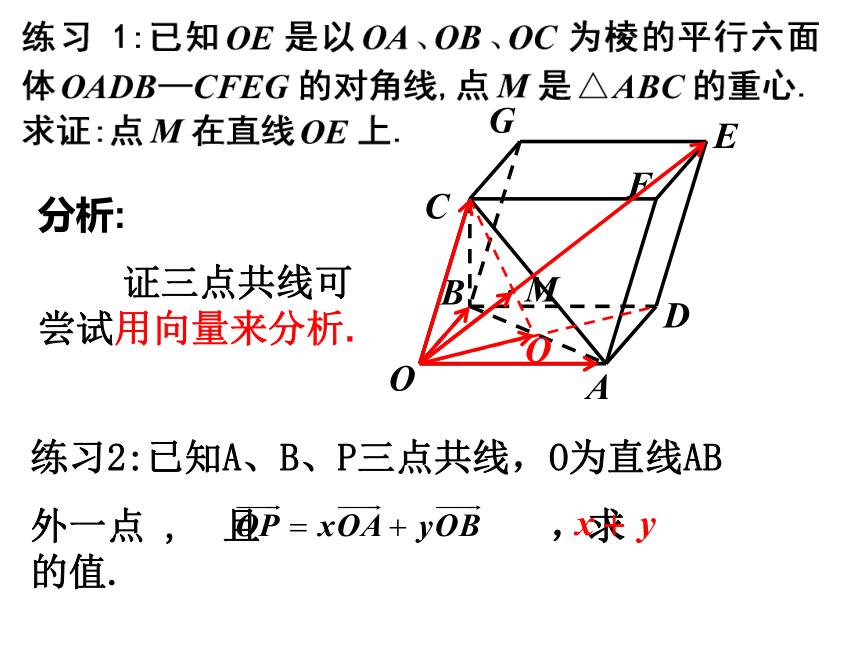
课时安排:1课时.思考分析:
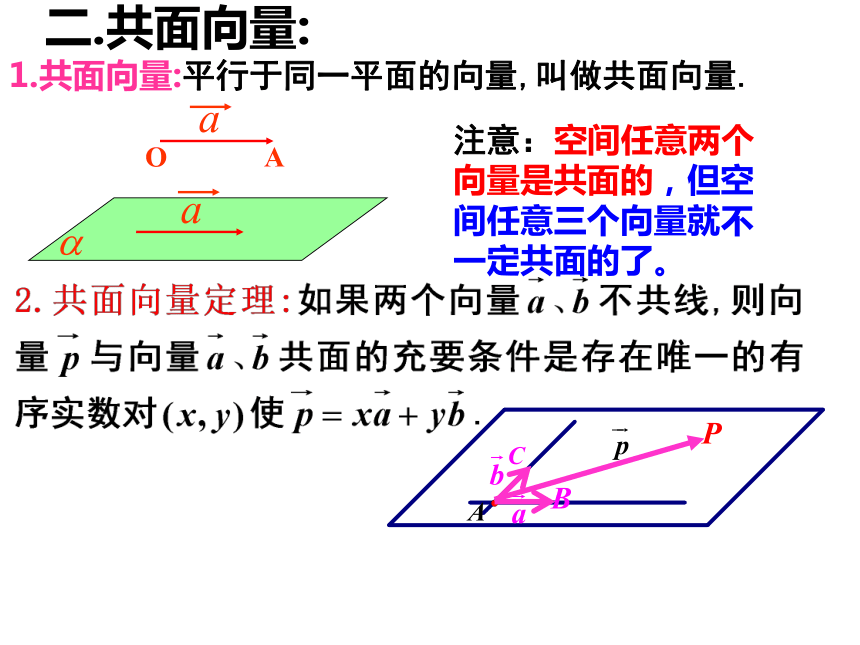
证三点共线可尝试用向量来分析.学习共面二.共面向量:1.共面向量:平行于同一平面的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。以
建立空间直角坐标系O—xyz若A(x1,y1,z1) , B(x2,y2,z2),
则证明:设正方体的棱长为1,建立如图的空间直角坐标系1.基本知识:(1)向量的长度公式与两点间的距离公式;(2)两个向量的夹角公式。 2.思想方法:用向量计算或证明几何问题
时,可以先建立直角坐标系,然后把向量、点坐
标化,借助向量的直角坐标运算法则进行计算或
证明。再见
⒉理解共面向量定理及其推论;掌握点在已知平面内的充要条件;
⒊会用上述知识解决立体几何中有关的简单问题.
教学重点:点在已知平面内的充要条件.共线、共面定理及其应用.
教学难点:对点在已知平面内的充要条件的理解与运用.
授课类型:新授课.
课时安排:1课时.思考分析:
证三点共线可尝试用向量来分析.学习共面二.共面向量:1.共面向量:平行于同一平面的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。以
建立空间直角坐标系O—xyz若A(x1,y1,z1) , B(x2,y2,z2),
则证明:设正方体的棱长为1,建立如图的空间直角坐标系1.基本知识:(1)向量的长度公式与两点间的距离公式;(2)两个向量的夹角公式。 2.思想方法:用向量计算或证明几何问题
时,可以先建立直角坐标系,然后把向量、点坐
标化,借助向量的直角坐标运算法则进行计算或
证明。再见
