高中数学人教A版考点练习(必修一):二次函数的解析式与图象性质
文档属性
| 名称 | 高中数学人教A版考点练习(必修一):二次函数的解析式与图象性质 |  | |
| 格式 | zip | ||
| 文件大小 | 663.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 17:46:48 | ||
图片预览



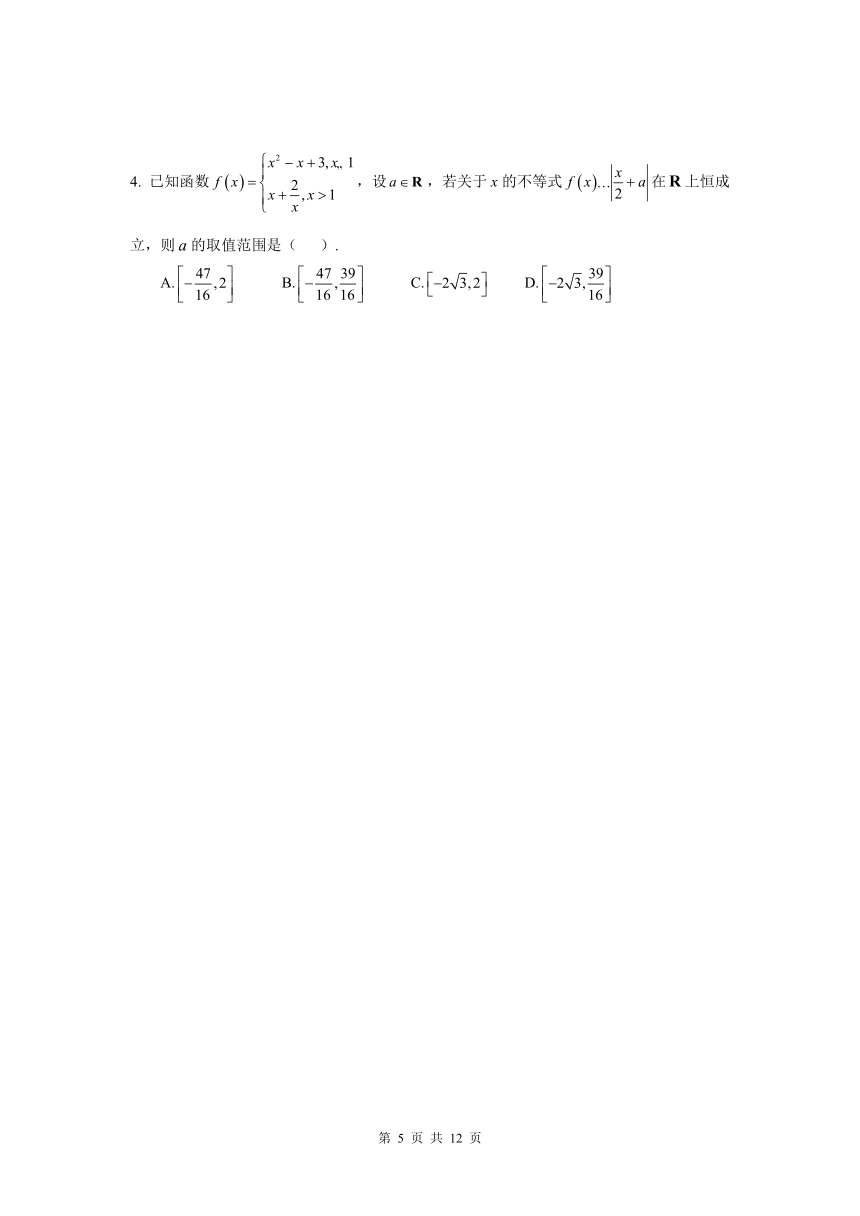
文档简介
二次函数的解析式与图象性质
一、二次函数的解析式
1. 已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,试确定该二次函数的解析式.
[来源:学#科#网]
2.已知二次函数f(x)是偶函数,且f(4)=4f(2)=16,则函数f(x)的解析式为________.
3.为了美观,在加工太阳镜时将下半部分轮廓制作成二次函数图象的形状(如图所示).若对应的两条曲线关于y轴对称,AE∥x轴,AB=4 cm,最低点C在x轴上,高CH=1 cm,BD=2 cm,则右轮廓线DFE所在的二次函数的解析式为( )
A.y=(x+3)2 B.y=-(x-3)2
C.y=-(x+3)2 D.y=(x-3)2
4. 对二次函数(为非零整数),四位同学分别给出下列结论,其中有且仅有一个结论是错误的,则错误的结论是( ).
A.是的零点 B.1是的极值点
C.3是的极值 D. 点在曲线上
二、二次函数的图象与性质
1. 若二次函数y=-2x2-4x+t的图象的顶点在x轴上,则t的值是( )
A.-4 B.4
C.-2 D.2
2.已知函数f(x)=ax2+2ax+b(1
C.f(x1)=f(x2)
D.f(x1)与f(x2)的大小关系不能确定
3. 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出下面四个结论:
①b2>4ac;②2a-b=1;③a-b+c=0;④5a
C.②③ D.①③
4.设二次函数f(x)=ax2-2ax+c在区间[0,1]上单调递减,且f(m)≤f(0),且实数m的取值范围是( )
A.(-∞,0] B.[2,+∞)
C.(-∞,0]∪[2,+∞) D.[0,2]
5. 设函数f(x)=则不等式f(x)>f(1)的解集是( )
A.(-3,1)∪(3,+∞) B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞) D.(-∞,-3)∪(1,3)
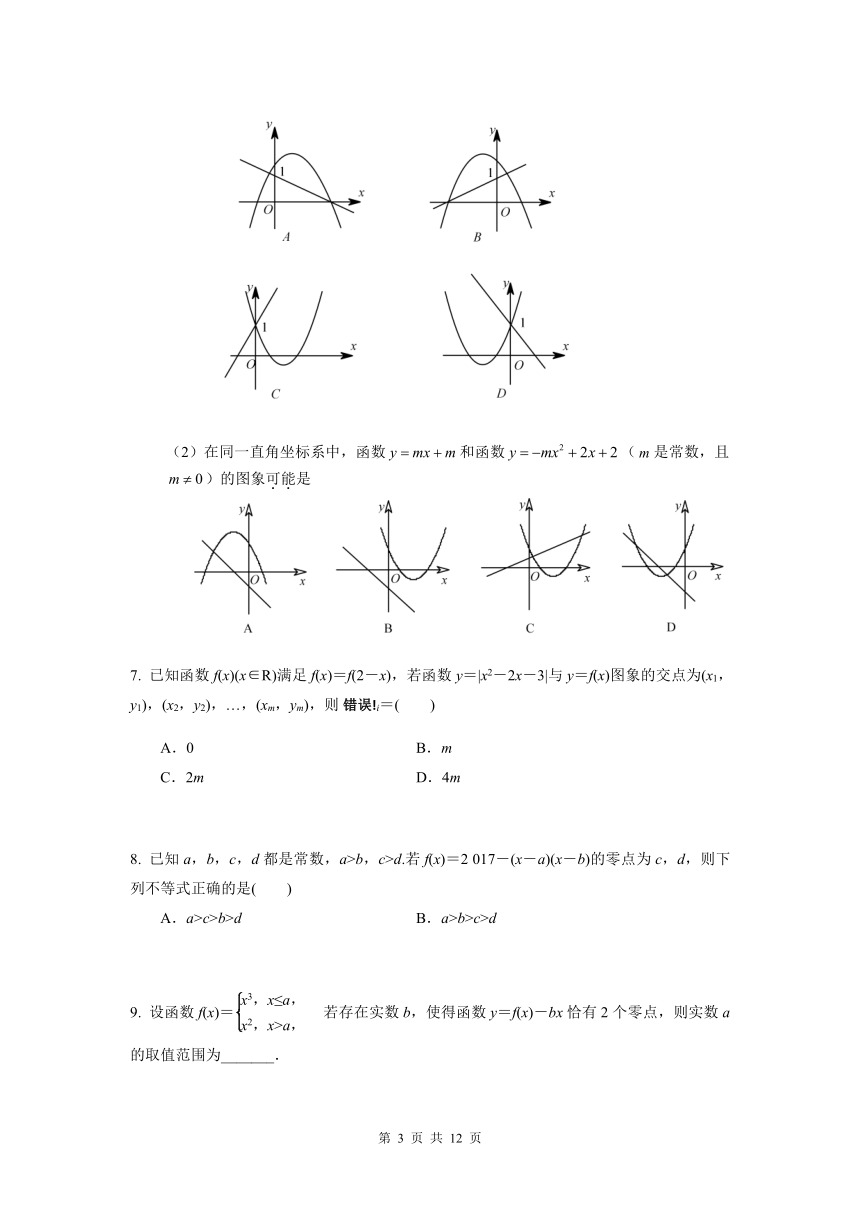
6. (1)函数与的图象可能是( )
(2)在同一直角坐标系中,函数和函数(是常数,且)的图象可能是
7. 已知函数f(x)(x∈R)满足f(x)=f(2-x),若函数y=|x2-2x-3|与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xm,ym),则i=( )
A.0 B.m
C.2m D.4m
8. 已知a,b,c,d都是常数,a>b,c>d.若f(x)=2 017-(x-a)(x-b)的零点为c,d,则下列不等式正确的是( )
A.a>c>b>d B.a>b>c>d
9. 设函数f(x)=若存在实数b,使得函数y=f(x)-bx恰有2个零点,则实数a的取值范围为_______.
10. 设a∈R,若x>0时均有[(a-1)x-1](x2-ax-1)≥0,则a=________.
11. 设函数f(x)=ax2+bx+c(a>b>c)的图象经过点A(m1,f(m1))和点B(m2,f(m2)),f(1)=0.若a2+[f(m1)+f(m2)]·a+f(m1)·f(m2)=0,则( )
A.b≥0 B.b<0
C.3a+c≤0 D.3a-c<0
12. 设函数f(x)=2ax2+2bx,若存在实数x0∈(0,t),使得对任意不为零的实数a,b,均有f(x0)=a+b成立,则t的取值范围是________.
13. 已知f(x)=m(x-2m)(x+m+3),g(x)=2x-2,若同时满足条件:
①?x∈R,f(x)<0或g(x)<0;
②?x∈(-∞,-4),f(x)g(x)<0.
则m的取值范围是________.
三、值域问题
1. 函数f(x)=-2x2+6x(-2≤x≤2)的值域是( )
A.[-20,4] B.(-20,4)
C. D.
2. 若二次函数f(x)=ax2-4x+c的值域为[0,+∞),则a,c满足的条件是________.
3. 若对任意a∈[-1,1],函数F(x)=x2+(a-4)x+4-2a的值恒大于零,则x的取值范围是( )
A.(1,3) B.(-∞,1)∪(3,+∞)
C.(1,2) D.(-∞,1)∪(2,+∞)
[来源:学科网]
4. 已知函数,设,若关于x的不等式在上恒成立,则的取值范围是( ).
A. B. C. D.
参考答案
二次函数的解析式与图象性质
一、二次函数的解析式
1. [解] 法一:用“一般式”解题设f(x)=ax2+bx+c(a≠0).
由题意得解得∴所求二次函数为f(x)=-4x2+4x+7.
法二:用“顶点式”解题
设f(x)=a(x-m)2+n(a≠0).∵f(2)=f(-1),∴抛物线的对称轴为x==,
∴m=.
又根据题意,函数有最大值8,∴n=8,
∴y=f(x)=a2+8.
∵f(2)=-1,∴a2+8=-1,解得a=-4,
∴f(x)=-42+8=-4x2+4x+7.
法三:用“零点式”解题
由已知f(x)+1=0的两根为x1=2,x2=-1,故可设f(x)+1=a(x-2)(x+1)(a≠0),
即f(x)=ax2-ax-2a-1. 又函数有最大值8,即=8.
解得a=-4或a=0(舍去).
∴所求函数的解析式为f(x)=-4x2+4x+7.
2. 解析:由题意可设函数f(x)=ax2+c(a≠0),则f(4)=16a+c=16,f(2)=4a+c=4,解得a=1,c=0,故f(x)=x2.
答案:f(x)=x2
3.解析:选D 由题图可知,对应的两条曲线关于y轴对称,AE∥x轴,AB=4 cm,最低点C在x轴上,高CH=1 cm,BD=2 cm,所以点C的纵坐标为0,横坐标的绝对值为3,即C(-3,0),因为点F与点C关于y轴对称,所以F(3,0),因为点F是右轮廓线DFE所在的二次函数图象的顶点,所以设该二次函数为y=a(x-3)2(a>0),将点D(1,1)代入得,a=,即y=(x-3)2.
4. 解析 观察四个选项会发现B,C这两个选项是“配套”的,所以以此为切入点,假设B,C正确,即为的顶点.由于抛物线开口向下时,D肯定错;抛物线开口向上时,A肯定错. 由此说明A与D中必有一个错误.假设A正确,
则有,与条件为整数矛盾,说明A错误. 故选A.
二、二次函数的图象与性质
1. 解析:选C ∵二次函数的图象的顶点在x轴上,∴Δ=16+8t=0,可得t=-2.
2. 解析:选A f(x)的对称轴为x=-1,因为1
若-1≤x1
3. 解析:选B ∵二次函数的图象与x轴交于两点,∴b2-4ac>0,即b2>4ac,①正确;
对称轴为x=-1,即-=-1,2a-b=0,②错误;
结合图象知,当x=-1时,y>0,即a-b+c>0,③错误;
由对称轴为x=-1知,b=2a,
又函数图象开口向下,∴a<0,∴5a<2a,即5a
4.解析:选D 二次函数f(x)=ax2-2ax+c在区间[0,1]上单调递减,则a≠0,f′(x)=2a(x-1)<0,x∈[0,1],所以a>0,即函数的图象开口向上,又因为对称轴是直线x=1.所以f(0)=f(2),则当f(m)≤f(0)时,有0≤m≤2.
5. 解析:选A ∵f(1)=3,∴不等式f(x)>f(1),即f(x)>3.
∴或解得x>3或-3
6. C D
7. 解析:选B ∵f(x)=f(2-x),∴函数f(x)的图象关于直线x=1对称.
又y=|x2-2x-3|=|(x-1)2-4|的图象关于直线x=1对称,∴两函数图象的交点关于直线x=1对称.
当m为偶数时,i=2×=m;
当m为奇数时,i=2×+1=m.故选B.
8. 解析:选D f(x)=2 017-(x-a)(x-b)=-x2+(a+b)x-ab+2 017,又f(a)=f(b)=2 017,c,d为函数f(x)的零点,且a>b,c>d, 所以可在平面直角坐标系中作出函数f(x)的大致图象,如图所示,由图可知c>a>b>d,故选D.
9. 解析:显然x=0是y=f(x)-bx的一个零点;
当x≠0时,令y=f(x)-bx=0得b=,
令g(x)==则b=g(x)存在唯一一个解.[来源:Zxxk.Com]
当a<0时,作出函数g(x)的图象,如图所示,
显然当a
若要使b=g(x)存在唯一一个解,则a>a2,即0
综上,a的取值范围是(-∞,0)∪(0,1).
答案:(-∞,0)∪(0,1)
10. 答案: [解析] 本题主要考查不等式的恒成立,不等式与方程的转化与应用问题,考查数形结合和转化化归的数学思想.令y1=x-1,y2=x2-ax-1,则函数y1=x-1,y2=x2-ax-1都过定点P.考查函数y1=x-1,令y=0,得M,同时只有a-1>0即a>1时才有可能满足x∈时,y1·y2≥0;
考查函数y2=x2-ax-1,显然只有过点M时才能满足x∈时,y1·y2≥0,代入得:2--1=0,可得2+a-1=0,2a2-3a=0解得a=或a=0,舍去a=0,得答案:a=.
11. 解析:选A 由f(1)=0可得a+b+c=0,若a≤0,由a>b>c,得a+b+c<0,这与a+b+c=0矛盾,故a>0,若c≥0,则有b>0,a>0,此时a+b+c>0,这与a+b+c=0矛盾;所以c<0成立,因为a2+[f(m1)+f(m2)]·a+f(m1)·f(m2)=0,所以(a+f(m1))(a+f(m2))=0,所以m1,m2是方程f(x)=-a的两个根,Δ=b2-4a(a+c)=b(b+4a)=b(3a-c)≥0,而a>0,c<0,所以3a-c>0,所以b≥0.
12. 解析:因为存在实数x0∈(0,t),使得对任意不为零的实数a,b,均有f(x0)=a+b成立,
所以2ax2+2bx=a+b等价于(2x-1)b=(1-2x2)a.
当x=时,左边=0,右边≠0,即等式不成立,故x≠;
当x≠时,(2x-1)b=(1-2x2)a等价于=,
设2x-1=k,因为x≠,所以k≠0,则x=,
则==. 设g(k)=,
则函数g(k)在(-1,0),(0,2t-1)上的值域为R.
又因为g(k)在(-∞,0),(0,+∞)上单调递减,
所以g(k)在(-1,0),(0,2t-1)上单调递减,
故当k∈(-1,0)时,g(k)
答案:(1,+∞)
13. 答案 (-4,-2) [解析] 本题考查函数图像与性质、不等式求解、逻辑、二次函数与指数函数等基础知识和基本技能.
满足条件①时,由g(x)=2x-2<0,可得x<1,要使?x∈R,f(x)<0或g(x)<0,必须使x≥1时,f(x)=m(x-2m)(x+m+3)<0恒成立,
当m=0时,f(x)=m(x-2m)(x+m+3)=0不满足条件,所以二次函数f(x)必须开口向下,也就是m<0,要满足条件,必须使方程f(x)=0的两根2m,-m-3都小于1,即可得m∈(-4,0).
满足条件②时,因为x∈(-∞,-4)时,g(x)<0,所以要使?x∈(-∞,-4)时,f(x)g(x)<0,只要?x0∈(-∞,-4)时,使f(x0)>0即可,只要使-4比2m,-m-3中较小的一个大即可,当m∈(-1,0)时,2m>-m-3,只要-4>-m-3,解得m>1与m∈(-1,0)的交集为空集;
当m=-1时,两根为-2;-2>-4,不符合;当m∈(-4,-1)时,2m<-m-3,所以只要-4>2m,
所以m∈(-4,-2).
综上可知m∈(-4,-2).
三、值域问题
1. 解析:选C 由函数f(x)=-2x2+6x可知,二次函数f(x)的图象开口向下,对称轴为x=,当-2≤x<时,函数f(x)单调递增,当≤x≤2时,函数f(x)单调递减,∴f(x)max=f=-2×+6×=,又f(-2)=-8-12=-20,f(2)=-8+12=4,∴函数f(x)的值域为.
2. 解析:由已知得?
答案:a>0,ac=4
3. 解析:选B 由题意,令f(a)=F(x)=x2+(a-4)x+4-2a=(x-2)a+x2-4x+4,对任意a∈[-1,1]恒成立,所以解得x<1或x>3.
4. 解析 解法一:易知,由不等式,得, 即,只需要计算在上的最大值和在上的最小值即可,
当时,(当时取等号),
(当时取等号),[来源:学.科.网]
所以;
当时,(当时取等号),
(当时取等号),
所以.
综上所述,得.故选A.
解法二:分别作出函数和的图像,如图所示.
若对于任意,恒成立,则满足且恒成立,即,又,当且仅当时,即时取等号,所以.
且,则,即.
综上所述,的取值范围为.故选A.
