高中数学统编版第一册第二章一元二次函数、方程和不等式2.2基本不等式课件(22张)
文档属性
| 名称 | 高中数学统编版第一册第二章一元二次函数、方程和不等式2.2基本不等式课件(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 873.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 09:14:34 | ||
图片预览








文档简介
课件22张PPT。2.2 基本不等式一二一、基本不等式 提示:当且仅当a=b时,等号成立. 提示:基本不等式可叙述为:两个正数的算术平均数不小于它们的几何平均数.一二(4)如图所示,AB是圆的直径,点C是AB上的一点,AC=a,BC=b.过点C作垂直于AB的弦DD',连接AD、BD.一二2.填空 一二二、利用基本不等式求最值
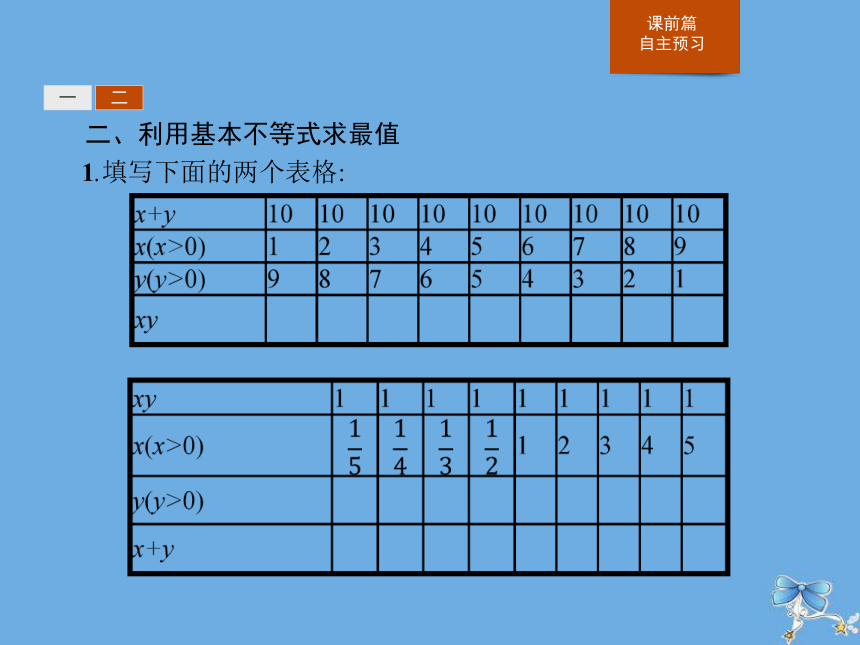
1.填写下面的两个表格:一二根据以上表格,并结合基本不等式分析:
(1)当x+y是定值时,xy有最大值还是最小值?最值等于什么?
(2)当xy是定值时,x+y有最大值还是最小值?最值等于什么?
提示:填表略,(1)当x+y是定值时,xy有最大值,且最大值等于一二2.填空
基本不等式与最值
已知x,y都是正数.一二3.做一做
已知x>0,y>0.
(1)若xy=4,则x+y的最小值是 ;?
(2)若x+y=4,则xy的最大值是 .?答案:(1)4 (2)4 探究一探究二探究三随堂演练基本不等式的理解
例1下列命题正确的是( ) 探究一探究二探究三随堂演练答案:B
反思感悟 应用基本不等式时要注意以下三点
(1)各项或各因式均为正;
(2)和或积为定值;
(3)各项或各因式能取得相等的值.即“一正二定三相等”.探究一探究二探究三随堂演练变式训练1下列结论不成立的是( )
A.若a,b∈R,则a10+b10≥2a5b5
D.若a∈R,则有a2+9≥6a
答案:C探究一探究二探究三随堂演练探究二利用基本不等式证明不等式 分析:(1)不等式的左边是和式,右边是带根号的积式之和,用基本不等式,将和变积,并证得不等式.(2)不等式右边的数字为8,使我们联想到对左边因式分别使用基本不等式,可得三个“2”连乘;
探究一探究二探究三随堂演练探究一探究二探究三随堂演练探究一探究二探究三随堂演练反思感悟 利用基本不等式证明不等式的注意事项
(1)利用基本不等式证明不等式,关键是所证不等式中必须有“和”式或“积”式,通过将“和”式转化为“积”式或将“积”式转化为“和”式,从而达到放缩的目的.
(2)注意多次运用基本不等式时等号能否取到.
(3)解题时要注意技巧,当不能直接利用基本不等式时,可将原不等式进行组合、构造,以满足能使用基本不等式的形式.
(4)在证明不等式的过程中,注意充分利用“1的代换”,即把常数“1”替换为已知的式子,然后经过整理后再利用基本不等式进行证明.探究一探究二探究三随堂演练变式训练2(1)已知a,b,c,d都是正数,求证:(ab+cd)(ac+bd)≥4abcd.探究一探究二探究三随堂演练探究三利用基本不等式求最值
例3(1)已知x>0,则 +x的最小值为( )
A.6 B.5 C.4 D.3
(2)已知a>0,b>0,且ab=1,则a+4b的最小值为 .?
答案:(1)A (2)4探究一探究二探究三随堂演练延伸探究 例题第(2)问,改为“已知a>0,b>0,且a+4b=4”,求ab的最大值.
探究一探究二探究三随堂演练答案:D A.最小值12 B.最大值12
C.最小值144 D.最大值144
答案:C探究一探究二探究三随堂演练答案:4 探究一探究二探究三随堂演练
1.填写下面的两个表格:一二根据以上表格,并结合基本不等式分析:
(1)当x+y是定值时,xy有最大值还是最小值?最值等于什么?
(2)当xy是定值时,x+y有最大值还是最小值?最值等于什么?
提示:填表略,(1)当x+y是定值时,xy有最大值,且最大值等于一二2.填空
基本不等式与最值
已知x,y都是正数.一二3.做一做
已知x>0,y>0.
(1)若xy=4,则x+y的最小值是 ;?
(2)若x+y=4,则xy的最大值是 .?答案:(1)4 (2)4 探究一探究二探究三随堂演练基本不等式的理解
例1下列命题正确的是( ) 探究一探究二探究三随堂演练答案:B
反思感悟 应用基本不等式时要注意以下三点
(1)各项或各因式均为正;
(2)和或积为定值;
(3)各项或各因式能取得相等的值.即“一正二定三相等”.探究一探究二探究三随堂演练变式训练1下列结论不成立的是( )
A.若a,b∈R,则a10+b10≥2a5b5
D.若a∈R,则有a2+9≥6a
答案:C探究一探究二探究三随堂演练探究二利用基本不等式证明不等式 分析:(1)不等式的左边是和式,右边是带根号的积式之和,用基本不等式,将和变积,并证得不等式.(2)不等式右边的数字为8,使我们联想到对左边因式分别使用基本不等式,可得三个“2”连乘;
探究一探究二探究三随堂演练探究一探究二探究三随堂演练探究一探究二探究三随堂演练反思感悟 利用基本不等式证明不等式的注意事项
(1)利用基本不等式证明不等式,关键是所证不等式中必须有“和”式或“积”式,通过将“和”式转化为“积”式或将“积”式转化为“和”式,从而达到放缩的目的.
(2)注意多次运用基本不等式时等号能否取到.
(3)解题时要注意技巧,当不能直接利用基本不等式时,可将原不等式进行组合、构造,以满足能使用基本不等式的形式.
(4)在证明不等式的过程中,注意充分利用“1的代换”,即把常数“1”替换为已知的式子,然后经过整理后再利用基本不等式进行证明.探究一探究二探究三随堂演练变式训练2(1)已知a,b,c,d都是正数,求证:(ab+cd)(ac+bd)≥4abcd.探究一探究二探究三随堂演练探究三利用基本不等式求最值
例3(1)已知x>0,则 +x的最小值为( )
A.6 B.5 C.4 D.3
(2)已知a>0,b>0,且ab=1,则a+4b的最小值为 .?
答案:(1)A (2)4探究一探究二探究三随堂演练延伸探究 例题第(2)问,改为“已知a>0,b>0,且a+4b=4”,求ab的最大值.
探究一探究二探究三随堂演练答案:D A.最小值12 B.最大值12
C.最小值144 D.最大值144
答案:C探究一探究二探究三随堂演练答案:4 探究一探究二探究三随堂演练
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
