6.3梯形的面积课件(17张ppt)
图片预览






文档简介
(共17张PPT)
梯形的面积
多边形的面积
出示情境:
提出问题:
过渡:这节课我们就来一起学习梯形的面积。
问题:回忆一下,我们是怎样推导出三角形面积的计算公式的?
车窗玻璃的形状是梯形!怎样求出它的面积呢?
你能用学过的方法推导出梯形的面积计算公式吗?
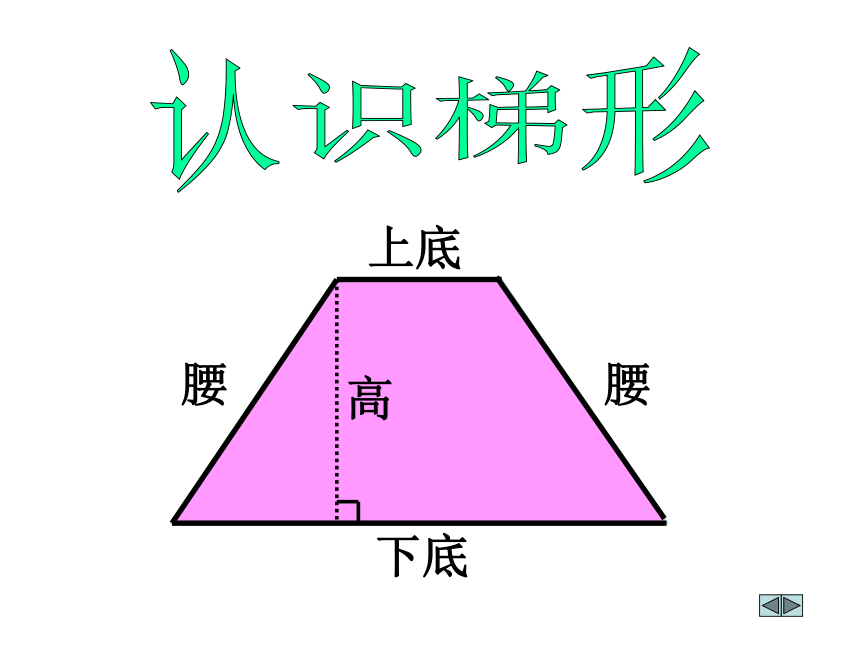
上底
下底
腰
腰
高
动手操作一
小组活动一:拼一拼
这两个梯形有什么特点?可以拼成一个什么图形?
拼成的图形的底与梯形的上底、下底有什么关系?高与梯形的高有什么关系?面积呢?
两个 梯形
完全一样的
梯形的下底
梯形的上底
1.平行四边形的底与梯形的底有什么关系?
高
2.平行四边形的高与梯形的高有什么关系?
平行四边形的底
?
?
答:平行四边形的底等于梯形 的上底与下底的和。
答:平行四边形的高等于梯形的高。
高
底 × 高
( + )
×
高
÷2
平行四边形的面积=
梯形的面积=
上底
下底
上底
下底
动手操作二
小组活动二:分一分
可以把梯形分成已学过的什么图形?
怎样求梯形的面积?
预设一:
梯形的面积=小三角形的面积+大三角形的面积
=上底×高÷2+下底×高÷2
上底
高
下底
=(上底+下底)×高÷2
预设二:
梯形的面积=平行四边形的面积+三角形的面积
=上底×高+(下底-上底)×高÷2
上底
高
下底
=(上底+下底)×高÷2
预设三
梯行的面积=平行四边形的面积
=底×高
=(上底+下底)×高÷2
(上底+下底)×高÷2
a
b
h
=
a
b
+
(
)
×
h
÷
2
S梯
解决问题,提升认识
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m2)
求下面每个梯形的面积(列式不用计算):
(1) ( 3 +4 )× 5 ÷ 2
4米
3米
5米
8厘米
5厘米
5.5厘米
1.2分米
15厘米
20厘米
(2) ( 5 +8 )× 5.5 ÷ 2
(3) ( 12 +15 )× 20 ÷ 2
巩固练习
判断题:
1.平行四边形的面积是梯形面积的2倍。( )
×
2.两个梯形一定可以拼成一个平行四边形。( )
×
观察下面的梯形,你发现了什么?
3cm
3cm
3cm
6cm
6cm
6cm
通过观察,我发现了上面三个梯形都是等底等高的,所以它们的面积也是一样的。
梯形的面积
多边形的面积
出示情境:
提出问题:
过渡:这节课我们就来一起学习梯形的面积。
问题:回忆一下,我们是怎样推导出三角形面积的计算公式的?
车窗玻璃的形状是梯形!怎样求出它的面积呢?
你能用学过的方法推导出梯形的面积计算公式吗?
上底
下底
腰
腰
高
动手操作一
小组活动一:拼一拼
这两个梯形有什么特点?可以拼成一个什么图形?
拼成的图形的底与梯形的上底、下底有什么关系?高与梯形的高有什么关系?面积呢?
两个 梯形
完全一样的
梯形的下底
梯形的上底
1.平行四边形的底与梯形的底有什么关系?
高
2.平行四边形的高与梯形的高有什么关系?
平行四边形的底
?
?
答:平行四边形的底等于梯形 的上底与下底的和。
答:平行四边形的高等于梯形的高。
高
底 × 高
( + )
×
高
÷2
平行四边形的面积=
梯形的面积=
上底
下底
上底
下底
动手操作二
小组活动二:分一分
可以把梯形分成已学过的什么图形?
怎样求梯形的面积?
预设一:
梯形的面积=小三角形的面积+大三角形的面积
=上底×高÷2+下底×高÷2
上底
高
下底
=(上底+下底)×高÷2
预设二:
梯形的面积=平行四边形的面积+三角形的面积
=上底×高+(下底-上底)×高÷2
上底
高
下底
=(上底+下底)×高÷2
预设三
梯行的面积=平行四边形的面积
=底×高
=(上底+下底)×高÷2
(上底+下底)×高÷2
a
b
h
=
a
b
+
(
)
×
h
÷
2
S梯
解决问题,提升认识
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m2)
求下面每个梯形的面积(列式不用计算):
(1) ( 3 +4 )× 5 ÷ 2
4米
3米
5米
8厘米
5厘米
5.5厘米
1.2分米
15厘米
20厘米
(2) ( 5 +8 )× 5.5 ÷ 2
(3) ( 12 +15 )× 20 ÷ 2
巩固练习
判断题:
1.平行四边形的面积是梯形面积的2倍。( )
×
2.两个梯形一定可以拼成一个平行四边形。( )
×
观察下面的梯形,你发现了什么?
3cm
3cm
3cm
6cm
6cm
6cm
通过观察,我发现了上面三个梯形都是等底等高的,所以它们的面积也是一样的。
