高中数学统编版第一册第四章指数函数与对数函数4.5.3函数模型的应用课件(29张)
文档属性
| 名称 | 高中数学统编版第一册第四章指数函数与对数函数4.5.3函数模型的应用课件(29张) |  | |
| 格式 | zip | ||
| 文件大小 | 913.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 17:52:24 | ||
图片预览








文档简介
课件29张PPT。4.5.3 函数模型的应用一二一、利用具体函数模型解决实际问题
1.除了上一章涉及到的数学模型,常见的数学模型还有哪些?
提示:利用具体函数解决实际问题是我们要关注的内容,具体函数的运用在生活中有很多体现,在学习完函数这部分内容以后,希望同学们能重点运用上一章提到的函数及指数函数和对数函数等常见函数来解决问题.下面是几种常见的函数模型:
(1)指数函数模型:f(x)=a·bx+c(a,b,c为常数,a≠0,b>0,且b≠1);
(2)对数函数模型:f(x)=mlogax+n(m,n,a为常数,m≠0,a>0,且a≠1);一二2.做一做
某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……现有2个这样的细胞,分裂x次后得到细胞的个数y与x的函数关系是( )
A.y=2x B.y=2x-1
C.y=2x D.y=2x+1
解析:分裂一次后由2个变成2×2=22(个),分裂两次后变成4×2=23(个),……,分裂x次后变成2x+1个.
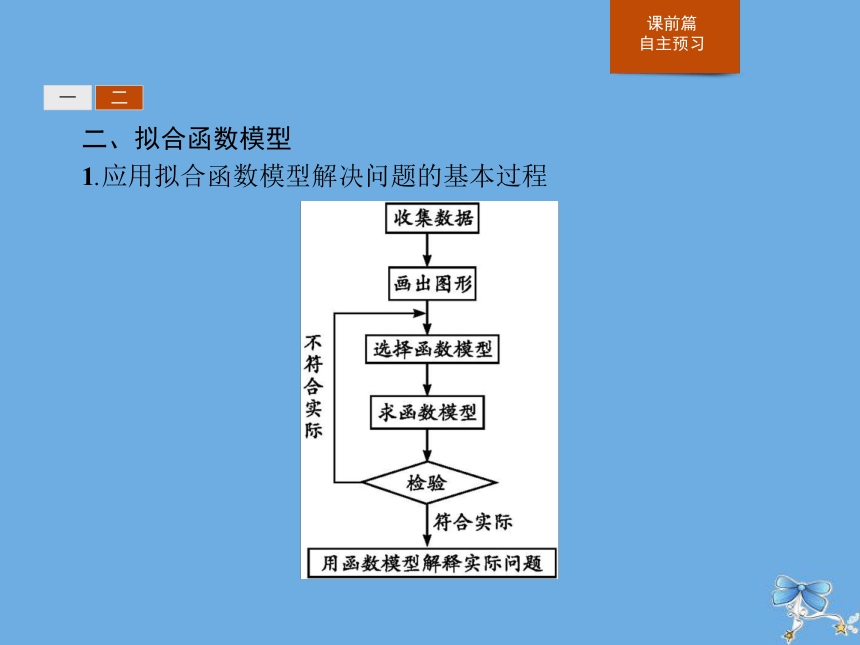
答案:D一二二、拟合函数模型
1.应用拟合函数模型解决问题的基本过程一二2.解答函数实际应用问题时,一般要分哪四步进行?
提示:第一步:分析、联想、转化、抽象;
第二步:建立函数模型,把实际应用问题转化为数学问题;
第三步:解答数学问题,求得结果;
第四步:把数学结果转译成具体问题的结论,做出解答.
而这四步中,最为关键的是把第二步处理好.只要把函数模型建立妥当,所有的问题即可在此基础上迎刃而解.一二3.做一做
“红豆生南国,春来发几枝.”图中给出了红豆生长时间t(月)与枝数y(枝)的散点图,那么红豆的枝数与生长时间的关系用下列哪个函数模型拟合最好?( )
A.指数函数y=2t
B.对数函数y=log2t
C.幂函数y=t3
D.二次函数y=2t2
解析:根据所给的散点图,观察可知图象在第一象限,且从左到右图象是上升的,并且增长速度越来越快,根据四个选项中函数的增长趋势可得,用指数函数模型拟合最好.
答案:A探究一探究二探究三随堂演练指数或对数函数模型的应用
例1 一片森林原来的面积为a,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
分析:可建立指数函数模型求解.探究一探究二探究三随堂演练解得n≤15.故今后最多还能砍伐15年. 探究一探究二探究三随堂演练反思感悟1.本题涉及平均增长率的问题,求解可用指数函数模型表示,通常可以表示为y=N·(1+p)x(其中N为原来的基础数,p为增长率,x为时间)的形式.
2.在实际问题中,有关人口增长、银行利率、细胞分裂等增长问题,都常用到指数函数模型.探究一探究二探究三随堂演练变式训练1为落实国家“精准扶贫”政策,让市民吃上放心蔬菜,某企业于2017年在其扶贫基地投入100万元研发资金,用于蔬菜的种植及开发,并计划今后十年内在此基础上每年投入的资金比上一年增长10%.
(1)写出第x年(2018年为第一年)该企业投入的资金数y(万元)与x的函数关系式,并指出函数的定义域;
(2)该企业从第几年开始(2018年为第一年),每年投入的资金数将超过200万元?
(参考数据lg 0.11≈-0.959,lg 1.1≈0.041,lg 11≈1.041,lg 2≈0.301)探究一探究二探究三随堂演练解:(1)第一年投入的资金数为100(1+10%)万元,
第二年投入的资金数为100(1+10%)+100(1+10%)10%=100(1+10%)2万元,
第x年(2018年为第一年)该企业投入的资金数y(万元)与x的函数关系式为y=100(1+10%)x万元,
其定义域为{x∈N*|x≤10}.
即企业从第8年开始(2018年为第一年),每年投入的资金数将超过200万元.探究一探究二探究三随堂演练对数函数模型
例2科学研究表明:人类对声音有不一样的感觉,这与声音的强度I(单位:瓦/平方米)有关.在实际测量时,常用L(单位:分贝)来表示声音强弱的等级,它与声音的强度I满足关系式: (a是常数),其中I0=1×10-12瓦/平方米.如风吹落叶沙沙声的强度I=1×10-11瓦/平方米,它的强弱等级L=10分贝.
(1)已知生活中几种声音的强度如下表:
求a和m的值;
(2)为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.探究一探究二探究三随堂演练分析:(1)根据条件代入关系式,即可求出a和m的值;
(2)解不等式L≤50即可.
即I≤105×10-12=10-7.
答:此时声音强度I的最大值为10-7瓦/平方米.探究一探究二探究三随堂演练反思感悟 (1)基本类型:有关对数函数模型的应用题一般都会给出函数解析式,然后根据实际问题再求解.
(2)求解策略:首先根据实际情况求出函数解析式中的参数,或给出具体情境,从中提炼出数据,代入解析式求值,然后根据数值回答其实际意义.探究一探究二探究三随堂演练变式训练2大西洋鲑鱼每年都要逆流而上,游回产地产卵.记鲑鱼的游速为v(单位:m/s),鲑鱼的耗氧量的单位数为Q,研究中发现v与
成正比,且当Q=900时,v=1.
(1)求出v关于Q的函数解析式;
(2)计算一条鲑鱼的游速是1.5 m/s时耗氧量的单位数;
(3)一条鲑鱼要想把游速提高1 m/s,其耗氧量的单位数应怎样变化?探究一探究二探究三随堂演练探究一探究二探究三随堂演练拟合函数模型的应用题
例3 为了估计山上积雪融化后对下游灌溉的影响,在山上建立了一个观察站,测量最大积雪深度x cm与当年灌溉面积y hm2.现有连续10年的实测资料,如下表所示:探究一探究二探究三随堂演练(1)描出灌溉面积y hm2随积雪深度x cm变化的数据点(x,y);
(2)建立一个能基本反映灌溉面积变化的函数模型y=f(x),并作出其图象;
(3)根据所建立的函数模型,若今年最大积雪深度为25 cm,则可以灌溉的土地面积是多少?
分析:首先根据表中数据描出各点,然后通过观察图象来判断问题所适用的函数模型.探究一探究二探究三随堂演练解:(1)数据点分布如图甲所示. 探究一探究二探究三随堂演练(2)从图甲中可以看到,数据点大致落在一条直线附近,由此,我们假设灌溉面积y hm2和最大积雪深度x cm满足线性函数模型y=a+bx(a,b为常数,b≠0).
取其中的两组数据(10.4,21.1),(24.0,45.8),用计算器可算得a≈2.4,b≈1.8.
这样,我们得到一个函数模型y=2.4+1.8x.作出函数图象如图乙,可以发现,这个函数模型与已知数据的拟合程度较好,这说明它能较好地反映最大积雪深度与灌溉面积的关系.
(3)由(2)得当x=25时,y=2.4+1.8×25=47.4,即当最大积雪深度为25 cm时,可以灌溉土地47.4 hm2.探究一探究二探究三随堂演练反思感悟 对于此类实际应用问题,关键是先建立适当的函数关系式,再解决数学问题,然后验证并结合问题的实际意义作出回答,这个过程就是先拟合函数再利用函数解题.函数拟合与预测的一般步骤是:
(1)能够根据原始数据、表格,描出数据点.
(2)通过数据点,画出“最贴近”的直线或曲线,即拟合直线或拟合曲线.如果所有实际点都落到了拟合直线或曲线上,滴“点”不漏,那么这将是个十分完美的事情,但在实际应用中,这种情况一般是不会发生的.因此,使实际点尽可能地均匀分布在直线或曲线两侧,得出的拟合直线或拟合曲线就是“最贴近”的了.
(3)根据所学函数知识,求出拟合直线或拟合曲线的函数关系式.
(4)利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依据.探究一探究二探究三随堂演练变式训练3某地区今年1月、2月、3月患某种传染病的人数分别为52,54,58.为了预测以后各月的患病人数,甲选择了模型y1=ax2+bx+c,乙选择了模型y2=p·qx+r,其中y1,y2为患病人数,x为月份数,a,b,c,p,q,r都是常数.结果4月、5月、6月份的患病人数分别为66,82,115,你认为谁选择的模型较好?探究一探究二探究三随堂演练②-①,得p·q2-p·q1=2,④
③-②,得p·q3-p·q2=4,⑤
⑤÷④,得q=2.
将q=2代入④式,得p=1.
将q=2,p=1代入①式,得r=50.
∴乙:y2=2x+50.
计算当x=4时,y1=64,y2=66;
当x=5时,y1=72,y2=82;
当x=6时,y1=82,y2=114.
可见,乙选择的模型较好.探究一探究二探究三随堂演练1.一辆汽车在某段路程中的行驶路程s关于时间t变化的图象如图所示,则图象所对应的函数模型是( )
A.分段函数 B.二次函数
C.指数函数 D.对数函数
解析:由题图知,在不同的时间段内,对应的图象不同,故对应函数模型应为分段函数.
答案:A探究一探究二探究三随堂演练2.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠面积增加数y关于年数x的函数关系较为近似的是( )解析:当x=1时,否定选项B;当x=3时,否定选项A,D,检验C项较为接近.
答案:C探究一探究二探究三随堂演练3.已知有A,B两个水桶,桶A中开始有a L水,桶A中的水不断流入桶B,t min后,桶A中剩余的水符合指数衰减曲线y1=ae-nt,那么桶B中的水就是y2=a-ae-nt(n为常数).假设5 min时,桶A和桶B中的水量相等,再过 min,桶A中的水只有 L.?
解析:因为5 min时,桶A和桶B中的水量相等,
所以a·e-5n=a-a·e-5n,答案:10 探究一探究二探究三随堂演练4.某工厂生产一种电脑元件,每月的生产数据如下表:
为估计以后每月该电脑元件的产量,以这三个月的产量为依据,用函数y=ax+b或y=ax+b(a,b为常数,且a>0)来模拟这种电脑元件的月产量y千件与月份的关系.请问:用以上哪个模拟函数较好?说明理由.探究一探究二探究三随堂演练解:若用函数y=ax+b(a≠0),取(1,50),(2,52),
∴y=2x+48.
当x=3时,y=54.
若用函数y=ax+b,取(1,50),(2,52),
当x=3时,y=56.
由题知3月份的产量为53.9千件,
由上可知用函数y=2x+48的估计误差较小,故用函数y=ax+b模拟比较好.
1.除了上一章涉及到的数学模型,常见的数学模型还有哪些?
提示:利用具体函数解决实际问题是我们要关注的内容,具体函数的运用在生活中有很多体现,在学习完函数这部分内容以后,希望同学们能重点运用上一章提到的函数及指数函数和对数函数等常见函数来解决问题.下面是几种常见的函数模型:
(1)指数函数模型:f(x)=a·bx+c(a,b,c为常数,a≠0,b>0,且b≠1);
(2)对数函数模型:f(x)=mlogax+n(m,n,a为常数,m≠0,a>0,且a≠1);一二2.做一做
某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……现有2个这样的细胞,分裂x次后得到细胞的个数y与x的函数关系是( )
A.y=2x B.y=2x-1
C.y=2x D.y=2x+1
解析:分裂一次后由2个变成2×2=22(个),分裂两次后变成4×2=23(个),……,分裂x次后变成2x+1个.
答案:D一二二、拟合函数模型
1.应用拟合函数模型解决问题的基本过程一二2.解答函数实际应用问题时,一般要分哪四步进行?
提示:第一步:分析、联想、转化、抽象;
第二步:建立函数模型,把实际应用问题转化为数学问题;
第三步:解答数学问题,求得结果;
第四步:把数学结果转译成具体问题的结论,做出解答.
而这四步中,最为关键的是把第二步处理好.只要把函数模型建立妥当,所有的问题即可在此基础上迎刃而解.一二3.做一做
“红豆生南国,春来发几枝.”图中给出了红豆生长时间t(月)与枝数y(枝)的散点图,那么红豆的枝数与生长时间的关系用下列哪个函数模型拟合最好?( )
A.指数函数y=2t
B.对数函数y=log2t
C.幂函数y=t3
D.二次函数y=2t2
解析:根据所给的散点图,观察可知图象在第一象限,且从左到右图象是上升的,并且增长速度越来越快,根据四个选项中函数的增长趋势可得,用指数函数模型拟合最好.
答案:A探究一探究二探究三随堂演练指数或对数函数模型的应用
例1 一片森林原来的面积为a,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
分析:可建立指数函数模型求解.探究一探究二探究三随堂演练解得n≤15.故今后最多还能砍伐15年. 探究一探究二探究三随堂演练反思感悟1.本题涉及平均增长率的问题,求解可用指数函数模型表示,通常可以表示为y=N·(1+p)x(其中N为原来的基础数,p为增长率,x为时间)的形式.
2.在实际问题中,有关人口增长、银行利率、细胞分裂等增长问题,都常用到指数函数模型.探究一探究二探究三随堂演练变式训练1为落实国家“精准扶贫”政策,让市民吃上放心蔬菜,某企业于2017年在其扶贫基地投入100万元研发资金,用于蔬菜的种植及开发,并计划今后十年内在此基础上每年投入的资金比上一年增长10%.
(1)写出第x年(2018年为第一年)该企业投入的资金数y(万元)与x的函数关系式,并指出函数的定义域;
(2)该企业从第几年开始(2018年为第一年),每年投入的资金数将超过200万元?
(参考数据lg 0.11≈-0.959,lg 1.1≈0.041,lg 11≈1.041,lg 2≈0.301)探究一探究二探究三随堂演练解:(1)第一年投入的资金数为100(1+10%)万元,
第二年投入的资金数为100(1+10%)+100(1+10%)10%=100(1+10%)2万元,
第x年(2018年为第一年)该企业投入的资金数y(万元)与x的函数关系式为y=100(1+10%)x万元,
其定义域为{x∈N*|x≤10}.
即企业从第8年开始(2018年为第一年),每年投入的资金数将超过200万元.探究一探究二探究三随堂演练对数函数模型
例2科学研究表明:人类对声音有不一样的感觉,这与声音的强度I(单位:瓦/平方米)有关.在实际测量时,常用L(单位:分贝)来表示声音强弱的等级,它与声音的强度I满足关系式: (a是常数),其中I0=1×10-12瓦/平方米.如风吹落叶沙沙声的强度I=1×10-11瓦/平方米,它的强弱等级L=10分贝.
(1)已知生活中几种声音的强度如下表:
求a和m的值;
(2)为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.探究一探究二探究三随堂演练分析:(1)根据条件代入关系式,即可求出a和m的值;
(2)解不等式L≤50即可.
即I≤105×10-12=10-7.
答:此时声音强度I的最大值为10-7瓦/平方米.探究一探究二探究三随堂演练反思感悟 (1)基本类型:有关对数函数模型的应用题一般都会给出函数解析式,然后根据实际问题再求解.
(2)求解策略:首先根据实际情况求出函数解析式中的参数,或给出具体情境,从中提炼出数据,代入解析式求值,然后根据数值回答其实际意义.探究一探究二探究三随堂演练变式训练2大西洋鲑鱼每年都要逆流而上,游回产地产卵.记鲑鱼的游速为v(单位:m/s),鲑鱼的耗氧量的单位数为Q,研究中发现v与
成正比,且当Q=900时,v=1.
(1)求出v关于Q的函数解析式;
(2)计算一条鲑鱼的游速是1.5 m/s时耗氧量的单位数;
(3)一条鲑鱼要想把游速提高1 m/s,其耗氧量的单位数应怎样变化?探究一探究二探究三随堂演练探究一探究二探究三随堂演练拟合函数模型的应用题
例3 为了估计山上积雪融化后对下游灌溉的影响,在山上建立了一个观察站,测量最大积雪深度x cm与当年灌溉面积y hm2.现有连续10年的实测资料,如下表所示:探究一探究二探究三随堂演练(1)描出灌溉面积y hm2随积雪深度x cm变化的数据点(x,y);
(2)建立一个能基本反映灌溉面积变化的函数模型y=f(x),并作出其图象;
(3)根据所建立的函数模型,若今年最大积雪深度为25 cm,则可以灌溉的土地面积是多少?
分析:首先根据表中数据描出各点,然后通过观察图象来判断问题所适用的函数模型.探究一探究二探究三随堂演练解:(1)数据点分布如图甲所示. 探究一探究二探究三随堂演练(2)从图甲中可以看到,数据点大致落在一条直线附近,由此,我们假设灌溉面积y hm2和最大积雪深度x cm满足线性函数模型y=a+bx(a,b为常数,b≠0).
取其中的两组数据(10.4,21.1),(24.0,45.8),用计算器可算得a≈2.4,b≈1.8.
这样,我们得到一个函数模型y=2.4+1.8x.作出函数图象如图乙,可以发现,这个函数模型与已知数据的拟合程度较好,这说明它能较好地反映最大积雪深度与灌溉面积的关系.
(3)由(2)得当x=25时,y=2.4+1.8×25=47.4,即当最大积雪深度为25 cm时,可以灌溉土地47.4 hm2.探究一探究二探究三随堂演练反思感悟 对于此类实际应用问题,关键是先建立适当的函数关系式,再解决数学问题,然后验证并结合问题的实际意义作出回答,这个过程就是先拟合函数再利用函数解题.函数拟合与预测的一般步骤是:
(1)能够根据原始数据、表格,描出数据点.
(2)通过数据点,画出“最贴近”的直线或曲线,即拟合直线或拟合曲线.如果所有实际点都落到了拟合直线或曲线上,滴“点”不漏,那么这将是个十分完美的事情,但在实际应用中,这种情况一般是不会发生的.因此,使实际点尽可能地均匀分布在直线或曲线两侧,得出的拟合直线或拟合曲线就是“最贴近”的了.
(3)根据所学函数知识,求出拟合直线或拟合曲线的函数关系式.
(4)利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依据.探究一探究二探究三随堂演练变式训练3某地区今年1月、2月、3月患某种传染病的人数分别为52,54,58.为了预测以后各月的患病人数,甲选择了模型y1=ax2+bx+c,乙选择了模型y2=p·qx+r,其中y1,y2为患病人数,x为月份数,a,b,c,p,q,r都是常数.结果4月、5月、6月份的患病人数分别为66,82,115,你认为谁选择的模型较好?探究一探究二探究三随堂演练②-①,得p·q2-p·q1=2,④
③-②,得p·q3-p·q2=4,⑤
⑤÷④,得q=2.
将q=2代入④式,得p=1.
将q=2,p=1代入①式,得r=50.
∴乙:y2=2x+50.
计算当x=4时,y1=64,y2=66;
当x=5时,y1=72,y2=82;
当x=6时,y1=82,y2=114.
可见,乙选择的模型较好.探究一探究二探究三随堂演练1.一辆汽车在某段路程中的行驶路程s关于时间t变化的图象如图所示,则图象所对应的函数模型是( )
A.分段函数 B.二次函数
C.指数函数 D.对数函数
解析:由题图知,在不同的时间段内,对应的图象不同,故对应函数模型应为分段函数.
答案:A探究一探究二探究三随堂演练2.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠面积增加数y关于年数x的函数关系较为近似的是( )解析:当x=1时,否定选项B;当x=3时,否定选项A,D,检验C项较为接近.
答案:C探究一探究二探究三随堂演练3.已知有A,B两个水桶,桶A中开始有a L水,桶A中的水不断流入桶B,t min后,桶A中剩余的水符合指数衰减曲线y1=ae-nt,那么桶B中的水就是y2=a-ae-nt(n为常数).假设5 min时,桶A和桶B中的水量相等,再过 min,桶A中的水只有 L.?
解析:因为5 min时,桶A和桶B中的水量相等,
所以a·e-5n=a-a·e-5n,答案:10 探究一探究二探究三随堂演练4.某工厂生产一种电脑元件,每月的生产数据如下表:
为估计以后每月该电脑元件的产量,以这三个月的产量为依据,用函数y=ax+b或y=ax+b(a,b为常数,且a>0)来模拟这种电脑元件的月产量y千件与月份的关系.请问:用以上哪个模拟函数较好?说明理由.探究一探究二探究三随堂演练解:若用函数y=ax+b(a≠0),取(1,50),(2,52),
∴y=2x+48.
当x=3时,y=54.
若用函数y=ax+b,取(1,50),(2,52),
当x=3时,y=56.
由题知3月份的产量为53.9千件,
由上可知用函数y=2x+48的估计误差较小,故用函数y=ax+b模拟比较好.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
