高中数学统编版第一册第五章三角函数5.2.1三角函数的概念课件(30张)
文档属性
| 名称 | 高中数学统编版第一册第五章三角函数5.2.1三角函数的概念课件(30张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 20:24:58 | ||
图片预览










文档简介
课件30张PPT。5.2.1 三角函数的概念一二三一、三角函数的定义
1.在直角坐标系中,称以原点O为圆心,以单位长度为半径的圆为单位圆.
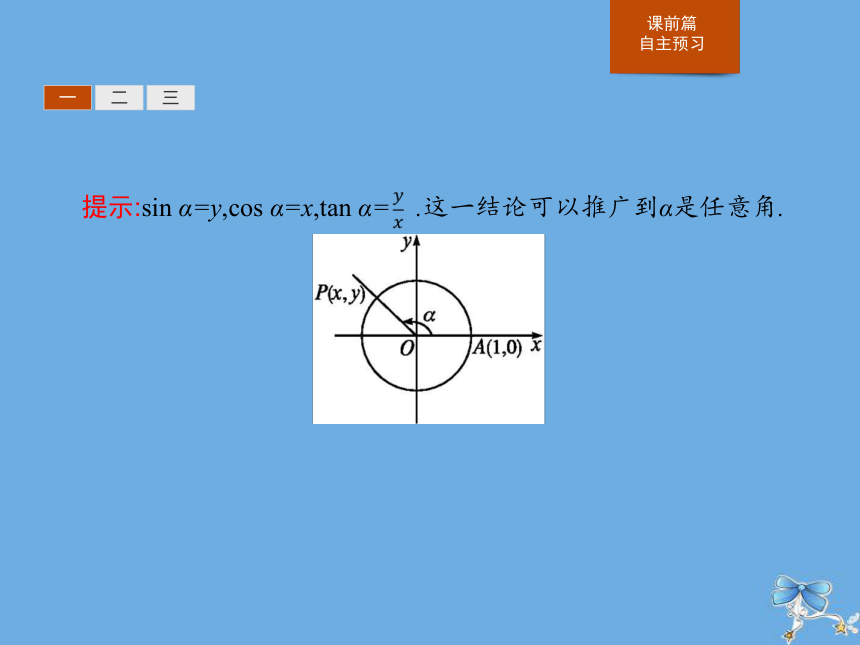
如图,如果一个锐角α的终边与单位圆的交点是P(x,y),根据初中所学在直角三角形中正弦、余弦、正切的定义,你能否用点P的坐标表示sin α,cos α,tan α?这一结论能否推广到α是任意角时的情形呢?一二三提示:sin α=y,cos α=x,tan α= .这一结论可以推广到α是任意角. 一二三2.填空
如图,α是任意角,以α的顶点O为坐标原点,以α的始边为x轴的正半轴,建立平面直角坐标系.
设P(x,y)是α的终边与单位圆的交点.
(1)把点P的纵坐标y叫做α的正弦函数,记作sin α,即y=sin α;
(2)把点P的横坐标x叫做α的余弦函数,记作cos α,即x=cos α;
(3)把点P的纵坐标与横坐标的比值 叫做α的正切,记作tan α,即 =tan α(x≠0).
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数.
3.填空一二三答案:B (2)如果在角α的终边上有一点M(3,4),那么如何求角α的三个三角函数值?一二三5.如果角α的终边落在y轴上,这时其终边与单位圆的交点坐标是什么?sin α,cos α,tan α的值是否还存在?
提示:终边与单位圆的交点坐标是(0,1)或(0,-1),这时tan α的值不存在,因为分母不能为零,但sin α,cos α的值仍然存在.6.填空
三角函数的定义域如下表所示.一二三二、三角函数值的符号
1.根据三角函数的定义,各个三角函数值是用单位圆上点的坐标表示的,当角在不同象限时,其与单位圆的交点坐标的符号就不同,因此其各个三角函数值的正负就不同,你能推导出sin α,cos α,tan α在不同象限内的符号吗?
提示:当α在第一象限时,sin α>0,cos α>0,tan α>0;当α在第二象限时,sin α>0,cos α<0,tan α<0;当α在第三象限时,sin α<0,cos α<0,tan α>0;当α在第四象限时,sin α<0,cos α>0,tan α<0.
2.sin α,cos α,tan α在各个象限的符号如下:
记忆口诀:“一全正,二正弦,三正切,四余弦”.一二三3.做一做
判断下列各三角函数值的符号:一二三三、诱导公式一
1.30°,390°,-330°三个角的终边有什么关系?它们与单位圆的交点坐标相同吗?这三个角的正弦值、余弦值、正切值相等吗?
提示:终边相同,与单位圆的交点坐标相同,三个角的正弦值、余弦值、正切值相等.
2.填空
诱导公式一
(1)语言表示:终边相同的角的同一三角函数的值相等.一二三探究一探究二探究三思维辨析随堂演练利用三角函数的定义求三角函数值
例1求解下列各题:
(3)已知角α的始边与x轴的非负半轴重合,终边在射线4x-3y=0(x≤0)上,则cos α-sin α= .?
分析:(1)先求出x的值,再计算;(2)利用三角函数的定义的推广求解;(3)先在终边上取点,再利用定义求解.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练反思感悟 利用三角函数的定义求一个角的三角函数值有以下几种情况:
(1)若已知角,则只需确定出该角的终边与单位圆的交点坐标,即可求出各三角函数值.
(4)若已知角α终边上点的坐标含参数,则需进行分类讨论.探究一探究二探究三思维辨析随堂演练判断三角函数值的符号
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
(2)判断下列各式的符号:
分析:(1)由已知条件确定出sin α,cos α的符号即可确定角α的象限;(2)先判断每个因式的符号,再确定积的符号.探究一探究二探究三思维辨析随堂演练(1)解析:由sin αtan α<0可知sin α,tan α异号,从而α为第二、第三象限角.由 可知cos α,tan α异号,从而α为第三、第四象限角.
综上可知,α为第三象限角,故选C.
答案:C
(2)解:①∵105°,230°分别为第二、第三象限角,
∴sin 105°>0,cos 230°<0.于是sin 105°·cos 230°<0.
探究一探究二探究三思维辨析随堂演练反思感悟 三角函数符号的判定:
对三角函数符号的判定,首先要判断角是第几象限角,然后根据规律:“一全正、二正弦、三正切、四余弦”,即可确定三角函数的符号.探究一探究二探究三思维辨析随堂演练变式训练1(1)已知α=2,则点P(sin α,tan α)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解析:因为 ,即α在第二象限,所以sin α>0,tan α<0,则点P(sin α,tan α)在第四象限.
答案:D
(2)已知角α的终边经过点(3a-9,a+2),且cos α≤0,sin α>0,则实数a的取值范围是( )
A.(-2,3] B.(-2,3) C.[-2,3) D.[-2,3]
解析:由cos α≤0,sin α>0可知,角α的终边在第二象限或y轴的正半轴上,所以有
答案:A探究一探究二探究三思维辨析随堂演练诱导公式一的应用
例3求下列各式的值:
(1)a2sin(-1 350°)+b2tan 405°-(a-b)2tan 765°-2abcos(-1 080°);
分析:将角转化为k·360°+α(k∈Z)或2kπ+α(k∈Z)的形式,利用公式一求值,注意熟记特殊角的三角函数值.
解:(1)原式=a2sin(-4×360°+90°)+b2tan(360°+45°)-(a-b)2tan(2×360°+45°)-2abcos(-3×360°)
=a2sin 90°+b2tan 45°-(a-b)2tan 45°-2abcos 0°
=a2+b2-(a-b)2-2ab=0.探究一探究二探究三思维辨析随堂演练反思感悟 诱导公式一的应用策略:
(1)诱导公式一可以统一写成f(k·360°+α)=f(α)或f(k·2π+α)=f(α)(k∈Z)的形式,它的实质是终边相同的角的同一三角函数值相等;
(2)利用它可把任意角的三角函数值转化为0~2π角的三角函数值,即可把负角的三角函数转化为0到2π间角的三角函数,亦可把大于2π的角的三角函数转化为0到2π间角的三角函数,即把角实现大化小,负化正的转化.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练忽视对参数的分类讨论致误
典例 角α的终边过点P(-3a,4a),a≠0,则cos α= .?
错解错在什么地方?你能发现吗?怎样避免这类错误呢?
提示:错解中,误以为a>0,没有对a的正负进行分类讨论,导致r求错,从而结果错误.探究一探究二探究三思维辨析随堂演练防范措施 在利用三角函数的定义解决问题时,如果终边上一点的坐标中含有参数,那么要注意对其进行分类讨论,以免丢解.探究一探究二探究三思维辨析随堂演练变式训练已知角α的终边在直线y=x上,则sin α=____.
解析:易知角α的终边在第一象限或第三象限,
当角α的终边在第一象限时,在角α的终边上取一点P(1,1),探究一探究二探究三思维辨析随堂演练答案:D 探究一探究二探究三思维辨析随堂演练答案:A 3.若tan θ·sin2θ<0,则角θ在( )
A.第一象限 B.第二象限
C.第二象限或第四象限 D.第二象限或第三象限
解析:因为tan θ·sin2θ<0,所以tan θ<0,于是角θ在第二象限或第四象限.
答案:C探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练
1.在直角坐标系中,称以原点O为圆心,以单位长度为半径的圆为单位圆.
如图,如果一个锐角α的终边与单位圆的交点是P(x,y),根据初中所学在直角三角形中正弦、余弦、正切的定义,你能否用点P的坐标表示sin α,cos α,tan α?这一结论能否推广到α是任意角时的情形呢?一二三提示:sin α=y,cos α=x,tan α= .这一结论可以推广到α是任意角. 一二三2.填空
如图,α是任意角,以α的顶点O为坐标原点,以α的始边为x轴的正半轴,建立平面直角坐标系.
设P(x,y)是α的终边与单位圆的交点.
(1)把点P的纵坐标y叫做α的正弦函数,记作sin α,即y=sin α;
(2)把点P的横坐标x叫做α的余弦函数,记作cos α,即x=cos α;
(3)把点P的纵坐标与横坐标的比值 叫做α的正切,记作tan α,即 =tan α(x≠0).
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数.
3.填空一二三答案:B (2)如果在角α的终边上有一点M(3,4),那么如何求角α的三个三角函数值?一二三5.如果角α的终边落在y轴上,这时其终边与单位圆的交点坐标是什么?sin α,cos α,tan α的值是否还存在?
提示:终边与单位圆的交点坐标是(0,1)或(0,-1),这时tan α的值不存在,因为分母不能为零,但sin α,cos α的值仍然存在.6.填空
三角函数的定义域如下表所示.一二三二、三角函数值的符号
1.根据三角函数的定义,各个三角函数值是用单位圆上点的坐标表示的,当角在不同象限时,其与单位圆的交点坐标的符号就不同,因此其各个三角函数值的正负就不同,你能推导出sin α,cos α,tan α在不同象限内的符号吗?
提示:当α在第一象限时,sin α>0,cos α>0,tan α>0;当α在第二象限时,sin α>0,cos α<0,tan α<0;当α在第三象限时,sin α<0,cos α<0,tan α>0;当α在第四象限时,sin α<0,cos α>0,tan α<0.
2.sin α,cos α,tan α在各个象限的符号如下:
记忆口诀:“一全正,二正弦,三正切,四余弦”.一二三3.做一做
判断下列各三角函数值的符号:一二三三、诱导公式一
1.30°,390°,-330°三个角的终边有什么关系?它们与单位圆的交点坐标相同吗?这三个角的正弦值、余弦值、正切值相等吗?
提示:终边相同,与单位圆的交点坐标相同,三个角的正弦值、余弦值、正切值相等.
2.填空
诱导公式一
(1)语言表示:终边相同的角的同一三角函数的值相等.一二三探究一探究二探究三思维辨析随堂演练利用三角函数的定义求三角函数值
例1求解下列各题:
(3)已知角α的始边与x轴的非负半轴重合,终边在射线4x-3y=0(x≤0)上,则cos α-sin α= .?
分析:(1)先求出x的值,再计算;(2)利用三角函数的定义的推广求解;(3)先在终边上取点,再利用定义求解.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练反思感悟 利用三角函数的定义求一个角的三角函数值有以下几种情况:
(1)若已知角,则只需确定出该角的终边与单位圆的交点坐标,即可求出各三角函数值.
(4)若已知角α终边上点的坐标含参数,则需进行分类讨论.探究一探究二探究三思维辨析随堂演练判断三角函数值的符号
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
(2)判断下列各式的符号:
分析:(1)由已知条件确定出sin α,cos α的符号即可确定角α的象限;(2)先判断每个因式的符号,再确定积的符号.探究一探究二探究三思维辨析随堂演练(1)解析:由sin αtan α<0可知sin α,tan α异号,从而α为第二、第三象限角.由 可知cos α,tan α异号,从而α为第三、第四象限角.
综上可知,α为第三象限角,故选C.
答案:C
(2)解:①∵105°,230°分别为第二、第三象限角,
∴sin 105°>0,cos 230°<0.于是sin 105°·cos 230°<0.
探究一探究二探究三思维辨析随堂演练反思感悟 三角函数符号的判定:
对三角函数符号的判定,首先要判断角是第几象限角,然后根据规律:“一全正、二正弦、三正切、四余弦”,即可确定三角函数的符号.探究一探究二探究三思维辨析随堂演练变式训练1(1)已知α=2,则点P(sin α,tan α)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解析:因为 ,即α在第二象限,所以sin α>0,tan α<0,则点P(sin α,tan α)在第四象限.
答案:D
(2)已知角α的终边经过点(3a-9,a+2),且cos α≤0,sin α>0,则实数a的取值范围是( )
A.(-2,3] B.(-2,3) C.[-2,3) D.[-2,3]
解析:由cos α≤0,sin α>0可知,角α的终边在第二象限或y轴的正半轴上,所以有
答案:A探究一探究二探究三思维辨析随堂演练诱导公式一的应用
例3求下列各式的值:
(1)a2sin(-1 350°)+b2tan 405°-(a-b)2tan 765°-2abcos(-1 080°);
分析:将角转化为k·360°+α(k∈Z)或2kπ+α(k∈Z)的形式,利用公式一求值,注意熟记特殊角的三角函数值.
解:(1)原式=a2sin(-4×360°+90°)+b2tan(360°+45°)-(a-b)2tan(2×360°+45°)-2abcos(-3×360°)
=a2sin 90°+b2tan 45°-(a-b)2tan 45°-2abcos 0°
=a2+b2-(a-b)2-2ab=0.探究一探究二探究三思维辨析随堂演练反思感悟 诱导公式一的应用策略:
(1)诱导公式一可以统一写成f(k·360°+α)=f(α)或f(k·2π+α)=f(α)(k∈Z)的形式,它的实质是终边相同的角的同一三角函数值相等;
(2)利用它可把任意角的三角函数值转化为0~2π角的三角函数值,即可把负角的三角函数转化为0到2π间角的三角函数,亦可把大于2π的角的三角函数转化为0到2π间角的三角函数,即把角实现大化小,负化正的转化.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练忽视对参数的分类讨论致误
典例 角α的终边过点P(-3a,4a),a≠0,则cos α= .?
错解错在什么地方?你能发现吗?怎样避免这类错误呢?
提示:错解中,误以为a>0,没有对a的正负进行分类讨论,导致r求错,从而结果错误.探究一探究二探究三思维辨析随堂演练防范措施 在利用三角函数的定义解决问题时,如果终边上一点的坐标中含有参数,那么要注意对其进行分类讨论,以免丢解.探究一探究二探究三思维辨析随堂演练变式训练已知角α的终边在直线y=x上,则sin α=____.
解析:易知角α的终边在第一象限或第三象限,
当角α的终边在第一象限时,在角α的终边上取一点P(1,1),探究一探究二探究三思维辨析随堂演练答案:D 探究一探究二探究三思维辨析随堂演练答案:A 3.若tan θ·sin2θ<0,则角θ在( )
A.第一象限 B.第二象限
C.第二象限或第四象限 D.第二象限或第三象限
解析:因为tan θ·sin2θ<0,所以tan θ<0,于是角θ在第二象限或第四象限.
答案:C探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
