高中数学统编版第一册第五章三角函数5.3诱导公式(第1课时)诱导公式二、三、四课件(25张)
文档属性
| 名称 | 高中数学统编版第一册第五章三角函数5.3诱导公式(第1课时)诱导公式二、三、四课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 20:25:41 | ||
图片预览






文档简介
课件25张PPT。第1课时 诱导公式二、三、四一二三一、诱导公式二
1.观察单位圆,回答下列问题:
(1)角α与角π+α的终边有什么关系?
(2)角α与角π+α的终边与单位圆的交点P,P1有什么对称关系?
(3)在(2)中,点P,P1的坐标有什么关系?
提示:(1)在一条直线上,方向相反;(2)关于原点对称;(3)横、纵坐标都互为相反数.一二三2.填空
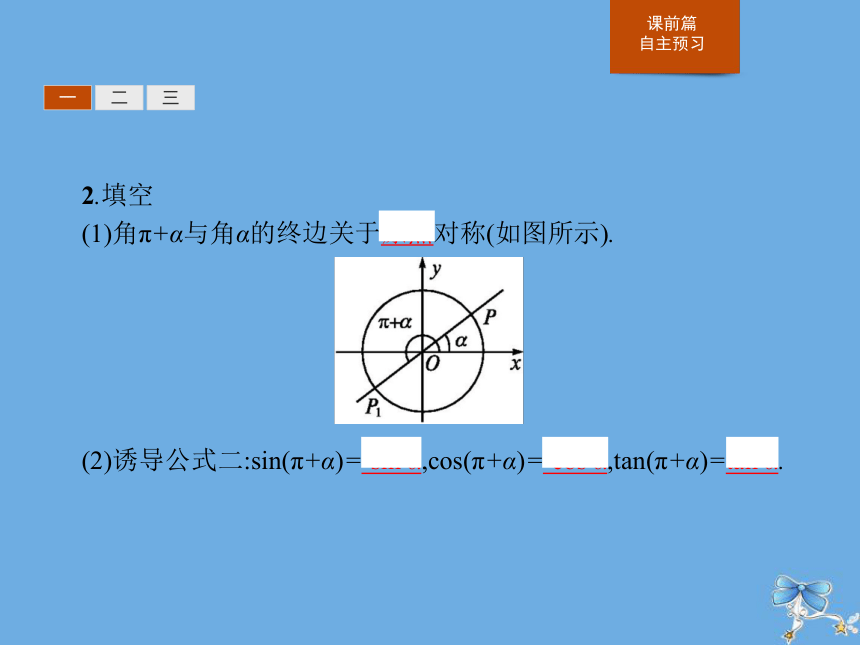
(1)角π+α与角α的终边关于原点对称(如图所示).
(2)诱导公式二:sin(π+α)=-sin α,cos(π+α)=-cos α,tan(π+α)=tan α.?一二三一二三二、诱导公式三
1.观察单位圆,回答下列问题:
(1)角α与角-α的终边有什么关系?
(2)角α与角-α的终边与单位圆的交点P,P1有什么对称关系?
(3)在(2)中,点P,P1的坐标有什么关系?
提示:(1)关于x轴对称;(2)关于x轴对称;(3)横坐标相等,纵坐标互为相反数.
2.填空
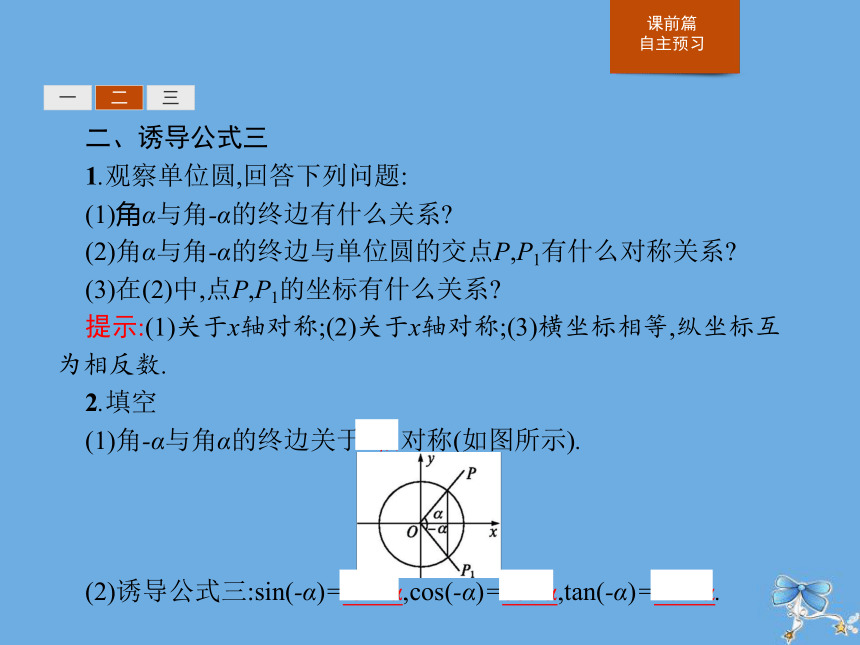
(1)角-α与角α的终边关于x轴对称(如图所示).
(2)诱导公式三:sin(-α)=-sin α,cos(-α)=cos α,tan(-α)=-tan α.?一二三一二三三、诱导公式四
1.观察单位圆,回答下列问题:
(1)角α与角π-α的终边有什么关系?
(2)角α与角π-α的终边与单位圆的交点P,P1有什么对称关系?
(3)在(2)中,点P,P1的坐标有什么关系?
提示:(1)关于y轴对称;(2)关于y轴对称;(3)横坐标互为相反数、纵坐标相等.一二三2.填空
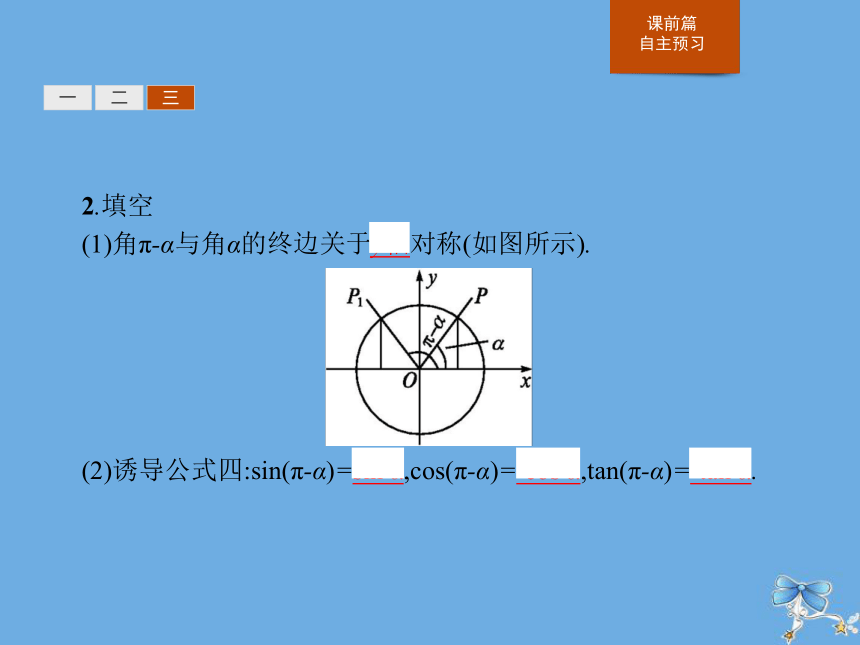
(1)角π-α与角α的终边关于y轴对称(如图所示).
(2)诱导公式四:sin(π-α)=sin α,cos(π-α)=-cos α,tan(π-α)=-tan α.?一二三探究一探究二探究三随堂演练利用诱导公式解决求值问题
例1(1)求sin 585°cos 1 290°+cos(-30°)sin 210°+tan 135°的值;
(2)已知cos(α-55°)=- ,且α为第四象限角,求sin(α+125°)的值.
分析:(1)利用诱导公式将负角化为正角,进而化为锐角进行求值;(2)寻求α-55°与α+125°之间的关系,利用诱导公式进行化简.探究一探究二探究三随堂演练解:(1)sin 585°cos 1 290°+cos(-30°)sin 210°+tan 135°
=sin(360°+225°)cos(3×360°+210°)+cos 30°sin 210°+tan(180°-45°)
=sin 225°cos 210°+cos 30°sin 210°-tan 45°
=sin(180°+45°)cos(180°+30°)+cos 30°·sin(180°+30°)-tan 45°
=sin 45°cos 30°-cos 30°sin 30°-tan 45°探究一探究二探究三随堂演练探究一探究二探究三随堂演练反思感悟 1.利用诱导公式解决给角求值问题的基本步骤:
2.利用诱导公式解决给值求值问题的策略:
(1)弄清楚已知条件与所求式中角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.探究一探究二探究三随堂演练延伸探究 本例(2)中,条件不变,如何求tan(595°-α)的值?探究一探究二探究三随堂演练利用诱导公式解决化简问题
分析:充分利用所学的四个诱导公式对角进行转化,并结合同角三角函数关系式进行化简.探究一探究二探究三随堂演练反思感悟 利用诱导公式一~四化简应注意的问题
(1)利用诱导公式主要是进行角的转化,从而达到统一角的目的.
(2)化简时函数名不发生改变,但一定要注意函数的符号有没有改变.
(3)同时有切(正切)与弦(正弦、余弦)的式子化简,一般采用切化弦,有时也将弦化切.探究一探究二探究三随堂演练探究一探究二探究三随堂演练利用诱导公式解决证明问题
分析:观察被证式两端,左繁右简,可以从左端入手,利用诱导公式进行化简,逐步地推向右边.探究一探究二探究三随堂演练反思感悟 关于三角恒等式的证明,常用方法:
(1)从一边开始,证得它等于另一边,一般由繁到简;
(2)左右归一法,即证明左右两边都等于同一个式子.无论用哪种方法都要针对题设与结论间的差异,有针对性地变形,以消除其差异.探究一探究二探究三随堂演练探究一探究二探究三随堂演练1.tan(-600°)的值等于( )
解析:tan(-600°)=-tan 600°=-tan(360°+240°)=-tan 240°=-tan(180°+60°)=-tan 60°=-
答案:B探究一探究二探究三随堂演练答案:C 探究一探究二探究三随堂演练答案:D 答案:-1 探究一探究二探究三随堂演练
1.观察单位圆,回答下列问题:
(1)角α与角π+α的终边有什么关系?
(2)角α与角π+α的终边与单位圆的交点P,P1有什么对称关系?
(3)在(2)中,点P,P1的坐标有什么关系?
提示:(1)在一条直线上,方向相反;(2)关于原点对称;(3)横、纵坐标都互为相反数.一二三2.填空
(1)角π+α与角α的终边关于原点对称(如图所示).
(2)诱导公式二:sin(π+α)=-sin α,cos(π+α)=-cos α,tan(π+α)=tan α.?一二三一二三二、诱导公式三
1.观察单位圆,回答下列问题:
(1)角α与角-α的终边有什么关系?
(2)角α与角-α的终边与单位圆的交点P,P1有什么对称关系?
(3)在(2)中,点P,P1的坐标有什么关系?
提示:(1)关于x轴对称;(2)关于x轴对称;(3)横坐标相等,纵坐标互为相反数.
2.填空
(1)角-α与角α的终边关于x轴对称(如图所示).
(2)诱导公式三:sin(-α)=-sin α,cos(-α)=cos α,tan(-α)=-tan α.?一二三一二三三、诱导公式四
1.观察单位圆,回答下列问题:
(1)角α与角π-α的终边有什么关系?
(2)角α与角π-α的终边与单位圆的交点P,P1有什么对称关系?
(3)在(2)中,点P,P1的坐标有什么关系?
提示:(1)关于y轴对称;(2)关于y轴对称;(3)横坐标互为相反数、纵坐标相等.一二三2.填空
(1)角π-α与角α的终边关于y轴对称(如图所示).
(2)诱导公式四:sin(π-α)=sin α,cos(π-α)=-cos α,tan(π-α)=-tan α.?一二三探究一探究二探究三随堂演练利用诱导公式解决求值问题
例1(1)求sin 585°cos 1 290°+cos(-30°)sin 210°+tan 135°的值;
(2)已知cos(α-55°)=- ,且α为第四象限角,求sin(α+125°)的值.
分析:(1)利用诱导公式将负角化为正角,进而化为锐角进行求值;(2)寻求α-55°与α+125°之间的关系,利用诱导公式进行化简.探究一探究二探究三随堂演练解:(1)sin 585°cos 1 290°+cos(-30°)sin 210°+tan 135°
=sin(360°+225°)cos(3×360°+210°)+cos 30°sin 210°+tan(180°-45°)
=sin 225°cos 210°+cos 30°sin 210°-tan 45°
=sin(180°+45°)cos(180°+30°)+cos 30°·sin(180°+30°)-tan 45°
=sin 45°cos 30°-cos 30°sin 30°-tan 45°探究一探究二探究三随堂演练探究一探究二探究三随堂演练反思感悟 1.利用诱导公式解决给角求值问题的基本步骤:
2.利用诱导公式解决给值求值问题的策略:
(1)弄清楚已知条件与所求式中角、函数名称及有关运算之间的差异及联系.
(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.探究一探究二探究三随堂演练延伸探究 本例(2)中,条件不变,如何求tan(595°-α)的值?探究一探究二探究三随堂演练利用诱导公式解决化简问题
分析:充分利用所学的四个诱导公式对角进行转化,并结合同角三角函数关系式进行化简.探究一探究二探究三随堂演练反思感悟 利用诱导公式一~四化简应注意的问题
(1)利用诱导公式主要是进行角的转化,从而达到统一角的目的.
(2)化简时函数名不发生改变,但一定要注意函数的符号有没有改变.
(3)同时有切(正切)与弦(正弦、余弦)的式子化简,一般采用切化弦,有时也将弦化切.探究一探究二探究三随堂演练探究一探究二探究三随堂演练利用诱导公式解决证明问题
分析:观察被证式两端,左繁右简,可以从左端入手,利用诱导公式进行化简,逐步地推向右边.探究一探究二探究三随堂演练反思感悟 关于三角恒等式的证明,常用方法:
(1)从一边开始,证得它等于另一边,一般由繁到简;
(2)左右归一法,即证明左右两边都等于同一个式子.无论用哪种方法都要针对题设与结论间的差异,有针对性地变形,以消除其差异.探究一探究二探究三随堂演练探究一探究二探究三随堂演练1.tan(-600°)的值等于( )
解析:tan(-600°)=-tan 600°=-tan(360°+240°)=-tan 240°=-tan(180°+60°)=-tan 60°=-
答案:B探究一探究二探究三随堂演练答案:C 探究一探究二探究三随堂演练答案:D 答案:-1 探究一探究二探究三随堂演练
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
