高中数学统编版第一册第五章三角函数5.6函数y=Asin(ωxφ)课件(39张)
文档属性
| 名称 | 高中数学统编版第一册第五章三角函数5.6函数y=Asin(ωxφ)课件(39张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 20:29:04 | ||
图片预览











文档简介
课件39张PPT。5.6 函数y=Asin(ωx+φ)一二三一、匀速圆周运动数学模型
1.填空
(1)三角函数数学模型在模拟一些周期现象时应用十分广泛,但一般都能概括为y=Asin(ωx+φ)+B或y=Acos(ωx+φ)+B的形式.
(2)三角函数作为描述现实世界中周期现象的一种数学模型,可以用来研究很多问题,在刻画周期规律、预测未来方面发挥着重要作用.一二三2.做一做
如图,点P是半径为r的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω(rad/s)做圆周运动,则点P的纵坐标y关于时间t的函数关系式为 .?
解析:当质点P从P0转到点P位置时,点P转过的角度为ωt,
则∠POx=ωt+φ,由任意角的三角函数定义知点P的纵坐标y=rsin(ωt+φ).
答案:y=rsin(ωt+φ)一二三3.判断正误
(1)三角函数是描述现实世界中周期变化现象的重要函数模型. ( )
(2)与周期有关的实际问题都必须用三角函数模型解决. ( )
答案:(1)√ (2)×一二三二、图象变换
1.φ对函数y=sin(x+φ),x∈R的图象的影响
提示:y=sin(x+φ)的图象可以由函数y=sin x的图象经过左右平移|φ|个单位得到.一二三(2)填空
如图,函数y=sin(x+φ)(φ≠0)的图象,可以看作是把y=sin x的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位长度得到的.一二三答案:B 一二三2.ω(ω>0)对函数y=sin(ωx+φ)的图象的影响
(1)在同一平面直角坐标系中,用“五点法”作出函数y=sin 2x与y=sin x的图象,从列表中变量的值以及画出的图象两个方面进行观察分析,y=sin(ωx+φ)的图象与y=sin(x+φ)的图象之间有什么关系?
提示:y=sin(ωx+φ)的图象可以由函数y=sin(x+φ)的图象经过左右伸缩变换得到.一二三(2)填空
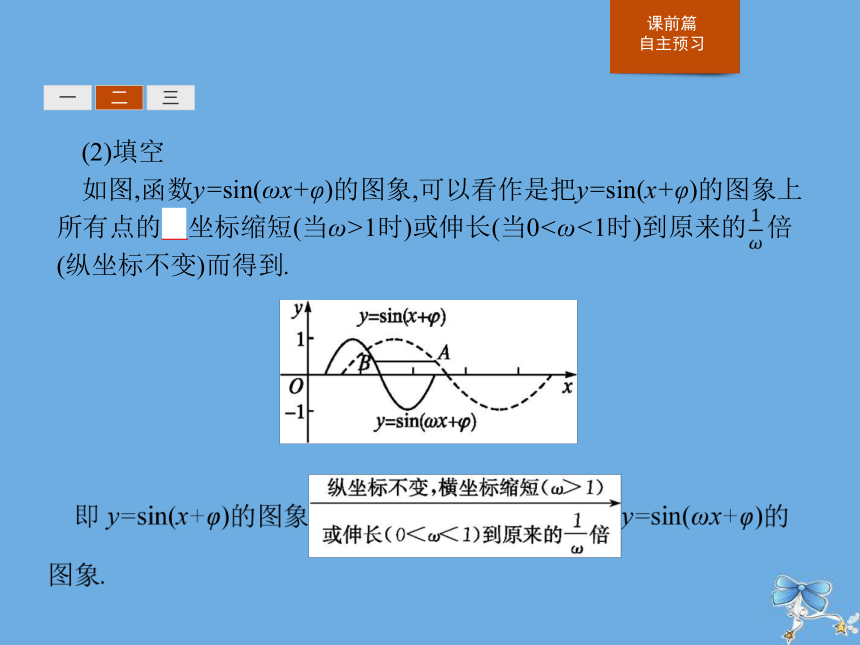
如图,函数y=sin(ωx+φ)的图象,可以看作是把y=sin(x+φ)的图象上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的 倍(纵坐标不变)而得到.一二三(3)做一做
函数y=sin 4x的图象可由函数y=sin x的图象经过怎样的变换得到( )
A.所有点的横坐标变为原来的4倍
解析:因为ω=4>1,所以可由y=sin x的图象上所有点的横坐标变为原来的 得到y=sin 4x的图象.
答案:B一二三3.A(A>0)对函数y=Asin(ωx+φ)的图象的影响
(1)在同一平面直角坐标系中,用“五点法”作出函数y=4sin x与y= sin x的图象,从列表中变量的值以及画出的图象两个方面进行观察分析,y=Asin(ωx+φ)的图象与y=sin(ωx+φ)的图象之间有什么关系?
提示:y=Asin(ωx+φ)的图象可以由函数y=sin(ωx+φ)的图象经过上下伸缩变换得到.一二三(2)填空
如图,函数y=Asin(ωx+φ)的图象,可以看作是把y=sin(ωx+φ)的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0(3)做一做
一二三三、函数y=Asin(ωx+φ)的图象的作法
1.作函数y=Asin(ωx+φ)的图象可有哪些方法?如果用图象变换法,那么是先平移后伸缩还是先伸缩后平移?
提示:作函数y=Asin(ωx+φ)的图象,可以用“五点法”,也可根据图象间的关系通过变换法得到;如果用图象变换法,那么既可以先平移后伸缩,也可以先伸缩后平移.
2.填空一二三(2)变换法:
由y=sin x的图象变换得到y=Asin(ωx+φ)的图象的方法如下:
①先平移后伸缩
②先伸缩后平移探究一探究二探究三思维辨析随堂演练匀速圆周运动的数学模型
例1一个大风车的半径为6 m,12 min旋转一周,它的最低点P0离地面2 m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间m(min)之间的函数关系式是( )
分析:由题意可设h(t)=Acos ωt+B,根据周期性 =12,由最大值与最小值分别为14,2,即可得出.探究一探究二探究三思维辨析随堂演练答案:D
反思感悟 匀速圆周运动的数学模型一般都归结为正弦型或余弦型函数形式.此类问题的切入点是初始位置及其半径、频率的值要明确,半径决定了振幅A,频率或周期能确定ω,初始位置不同对φ有影响.还要注意最大值与最小值与函数中参数的关系.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练答案:C 探究一探究二探究三思维辨析随堂演练用“五点法”作函数y=Asin(ωx+φ)的图象探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练反思感悟 1.“五点法”作图的实质
利用“五点法”作函数y=Asin(ωx+φ)的图象,实质是利用函数的三个零点及两个最值点画出函数在一个周期内的图象.
2.用“五点法”作函数y=Asin(ωx+φ)图象的步骤
第一步:列表.
第二步:在同一平面直角坐标系中描出各点.
第三步:用光滑曲线连接这些点,得到图象.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练函数y=Asin(ωx+φ)的图象变换
角度1 图象的变换方式
例3由函数y=sin x的图象经过怎样的变换,可以得到函数分析:本题考查三角函数的图象变换问题,可以从先“平移变换”或先“伸缩变换”两种不同变换顺序的角度去考虑,得到答案.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练角度2 求函数的解析式
例4把函数y=sin(ωx+φ)(ω>0,|φ|<π)的图象向左平移 个单位长度,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得图象的函数解析式为y=sin x,则( )
分析:确定逆向变换过程→由伸缩变换确定ω→由平移变换确定φ→确定函数解析式探究一探究二探究三思维辨析随堂演练答案:B 探究一探究二探究三思维辨析随堂演练反思感悟 1.对函数y=Asin(ωx+φ)+k(A>0,ω>0,φ≠0,k≠0),其图象的基本变换有:
①振幅变换(纵向伸缩变换):是由A的变化引起的,A>1时伸长,A<1时缩短.
②周期变换(横向伸缩变换):是由ω的变化引起的,ω>1时缩短,ω<1时伸长.
③相位变换(横向平移变换):是由φ引起的,φ>0时左移,φ<0时右移.
④上下平移(纵向平移变换):是由k引起的,k>0时上移,k<0时下移.
可以使用“先伸缩后平移”或“先平移后伸缩”两种方法来进行变换.
2.若相应变换的函数名不同时,先利用诱导公式将函数名化一致,再利用相应的变换得到结论.
3.由y=Asin(ωx+φ)+k(A>0,ω>0,φ≠0,k≠0)的图象得到y=sin x的图象,可采用逆向思维,将原变换反过来逆推得到.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练三角函数图象平移变换规则不清致误 探究一探究二探究三思维辨析随堂演练错解错在什么地方?你能发现吗?怎样避免这类错误呢?
提示:错解中有3个错误点:①审题不清,没有弄清楚哪一个函数图象移动变换得另一个函数图象.②平移方向上应该是“左加右减”,在错解中,由 的图象时应该向右平移.③平移的单位长度由于忽视了x的系数导致错误.
答案:C探究一探究二探究三思维辨析随堂演练防范措施 在解决三角函数图象的平移变换时,注意以下几点:
(1)平移之前应先将函数解析式化为同名的函数;
(2)弄清楚平移的方向,即平移哪个函数的图象,得到哪个函数的图象要清楚;
(3)平移的单位数是针对单一自变量x而言的,不是ωx+φ中的φ,而是 .探究一探究二探究三思维辨析随堂演练答案:B 探究一探究二探究三思维辨析随堂演练2.将函数y=sin 2x的图象向右平移 个单位长度,所得图象对应的函数是( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.非奇非偶函数
答案:A探究一探究二探究三思维辨析随堂演练3.将函数y=sin x的图象上所有点的横坐标缩短到原来的 (纵坐标不变)得 的图象.?
解析:依题意知,将y=sin x图象上所有点的横坐标缩短到原来的 后,可得y=sin 6x的图象.
答案:y=sin 6x探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练
1.填空
(1)三角函数数学模型在模拟一些周期现象时应用十分广泛,但一般都能概括为y=Asin(ωx+φ)+B或y=Acos(ωx+φ)+B的形式.
(2)三角函数作为描述现实世界中周期现象的一种数学模型,可以用来研究很多问题,在刻画周期规律、预测未来方面发挥着重要作用.一二三2.做一做
如图,点P是半径为r的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω(rad/s)做圆周运动,则点P的纵坐标y关于时间t的函数关系式为 .?
解析:当质点P从P0转到点P位置时,点P转过的角度为ωt,
则∠POx=ωt+φ,由任意角的三角函数定义知点P的纵坐标y=rsin(ωt+φ).
答案:y=rsin(ωt+φ)一二三3.判断正误
(1)三角函数是描述现实世界中周期变化现象的重要函数模型. ( )
(2)与周期有关的实际问题都必须用三角函数模型解决. ( )
答案:(1)√ (2)×一二三二、图象变换
1.φ对函数y=sin(x+φ),x∈R的图象的影响
提示:y=sin(x+φ)的图象可以由函数y=sin x的图象经过左右平移|φ|个单位得到.一二三(2)填空
如图,函数y=sin(x+φ)(φ≠0)的图象,可以看作是把y=sin x的图象上所有的点向左(当φ>0时)或向右(当φ<0时)平行移动|φ|个单位长度得到的.一二三答案:B 一二三2.ω(ω>0)对函数y=sin(ωx+φ)的图象的影响
(1)在同一平面直角坐标系中,用“五点法”作出函数y=sin 2x与y=sin x的图象,从列表中变量的值以及画出的图象两个方面进行观察分析,y=sin(ωx+φ)的图象与y=sin(x+φ)的图象之间有什么关系?
提示:y=sin(ωx+φ)的图象可以由函数y=sin(x+φ)的图象经过左右伸缩变换得到.一二三(2)填空
如图,函数y=sin(ωx+φ)的图象,可以看作是把y=sin(x+φ)的图象上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的 倍(纵坐标不变)而得到.一二三(3)做一做
函数y=sin 4x的图象可由函数y=sin x的图象经过怎样的变换得到( )
A.所有点的横坐标变为原来的4倍
解析:因为ω=4>1,所以可由y=sin x的图象上所有点的横坐标变为原来的 得到y=sin 4x的图象.
答案:B一二三3.A(A>0)对函数y=Asin(ωx+φ)的图象的影响
(1)在同一平面直角坐标系中,用“五点法”作出函数y=4sin x与y= sin x的图象,从列表中变量的值以及画出的图象两个方面进行观察分析,y=Asin(ωx+φ)的图象与y=sin(ωx+φ)的图象之间有什么关系?
提示:y=Asin(ωx+φ)的图象可以由函数y=sin(ωx+φ)的图象经过上下伸缩变换得到.一二三(2)填空
如图,函数y=Asin(ωx+φ)的图象,可以看作是把y=sin(ωx+φ)的图象上所有点的纵坐标伸长(当A>1时)或缩短(当0
一二三三、函数y=Asin(ωx+φ)的图象的作法
1.作函数y=Asin(ωx+φ)的图象可有哪些方法?如果用图象变换法,那么是先平移后伸缩还是先伸缩后平移?
提示:作函数y=Asin(ωx+φ)的图象,可以用“五点法”,也可根据图象间的关系通过变换法得到;如果用图象变换法,那么既可以先平移后伸缩,也可以先伸缩后平移.
2.填空一二三(2)变换法:
由y=sin x的图象变换得到y=Asin(ωx+φ)的图象的方法如下:
①先平移后伸缩
②先伸缩后平移探究一探究二探究三思维辨析随堂演练匀速圆周运动的数学模型
例1一个大风车的半径为6 m,12 min旋转一周,它的最低点P0离地面2 m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间m(min)之间的函数关系式是( )
分析:由题意可设h(t)=Acos ωt+B,根据周期性 =12,由最大值与最小值分别为14,2,即可得出.探究一探究二探究三思维辨析随堂演练答案:D
反思感悟 匀速圆周运动的数学模型一般都归结为正弦型或余弦型函数形式.此类问题的切入点是初始位置及其半径、频率的值要明确,半径决定了振幅A,频率或周期能确定ω,初始位置不同对φ有影响.还要注意最大值与最小值与函数中参数的关系.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练答案:C 探究一探究二探究三思维辨析随堂演练用“五点法”作函数y=Asin(ωx+φ)的图象探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练反思感悟 1.“五点法”作图的实质
利用“五点法”作函数y=Asin(ωx+φ)的图象,实质是利用函数的三个零点及两个最值点画出函数在一个周期内的图象.
2.用“五点法”作函数y=Asin(ωx+φ)图象的步骤
第一步:列表.
第二步:在同一平面直角坐标系中描出各点.
第三步:用光滑曲线连接这些点,得到图象.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练函数y=Asin(ωx+φ)的图象变换
角度1 图象的变换方式
例3由函数y=sin x的图象经过怎样的变换,可以得到函数分析:本题考查三角函数的图象变换问题,可以从先“平移变换”或先“伸缩变换”两种不同变换顺序的角度去考虑,得到答案.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练角度2 求函数的解析式
例4把函数y=sin(ωx+φ)(ω>0,|φ|<π)的图象向左平移 个单位长度,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得图象的函数解析式为y=sin x,则( )
分析:确定逆向变换过程→由伸缩变换确定ω→由平移变换确定φ→确定函数解析式探究一探究二探究三思维辨析随堂演练答案:B 探究一探究二探究三思维辨析随堂演练反思感悟 1.对函数y=Asin(ωx+φ)+k(A>0,ω>0,φ≠0,k≠0),其图象的基本变换有:
①振幅变换(纵向伸缩变换):是由A的变化引起的,A>1时伸长,A<1时缩短.
②周期变换(横向伸缩变换):是由ω的变化引起的,ω>1时缩短,ω<1时伸长.
③相位变换(横向平移变换):是由φ引起的,φ>0时左移,φ<0时右移.
④上下平移(纵向平移变换):是由k引起的,k>0时上移,k<0时下移.
可以使用“先伸缩后平移”或“先平移后伸缩”两种方法来进行变换.
2.若相应变换的函数名不同时,先利用诱导公式将函数名化一致,再利用相应的变换得到结论.
3.由y=Asin(ωx+φ)+k(A>0,ω>0,φ≠0,k≠0)的图象得到y=sin x的图象,可采用逆向思维,将原变换反过来逆推得到.探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练三角函数图象平移变换规则不清致误 探究一探究二探究三思维辨析随堂演练错解错在什么地方?你能发现吗?怎样避免这类错误呢?
提示:错解中有3个错误点:①审题不清,没有弄清楚哪一个函数图象移动变换得另一个函数图象.②平移方向上应该是“左加右减”,在错解中,由 的图象时应该向右平移.③平移的单位长度由于忽视了x的系数导致错误.
答案:C探究一探究二探究三思维辨析随堂演练防范措施 在解决三角函数图象的平移变换时,注意以下几点:
(1)平移之前应先将函数解析式化为同名的函数;
(2)弄清楚平移的方向,即平移哪个函数的图象,得到哪个函数的图象要清楚;
(3)平移的单位数是针对单一自变量x而言的,不是ωx+φ中的φ,而是 .探究一探究二探究三思维辨析随堂演练答案:B 探究一探究二探究三思维辨析随堂演练2.将函数y=sin 2x的图象向右平移 个单位长度,所得图象对应的函数是( )
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.非奇非偶函数
答案:A探究一探究二探究三思维辨析随堂演练3.将函数y=sin x的图象上所有点的横坐标缩短到原来的 (纵坐标不变)得 的图象.?
解析:依题意知,将y=sin x图象上所有点的横坐标缩短到原来的 后,可得y=sin 6x的图象.
答案:y=sin 6x探究一探究二探究三思维辨析随堂演练探究一探究二探究三思维辨析随堂演练
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
