高中数学统编版第一册第一章集合与常用逻辑用语1.4充分条件与必要条件课件(18张)
文档属性
| 名称 | 高中数学统编版第一册第一章集合与常用逻辑用语1.4充分条件与必要条件课件(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 355.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-25 20:31:39 | ||
图片预览






文档简介
课件18张PPT。1.4 充分条件与必要条件一二一、充分条件与必要条件
1.(1)已知“若p,则q”为真命题,说明p与q之间有什么关系?
提示:说明当p成立时,一定能得出q成立.即由p通过推理可以得出q.这时我们就说,由p可以推出q,记作p?q.
(2)类似地,如果“若p,则q”为假命题,说明p与q之间有什么关系?
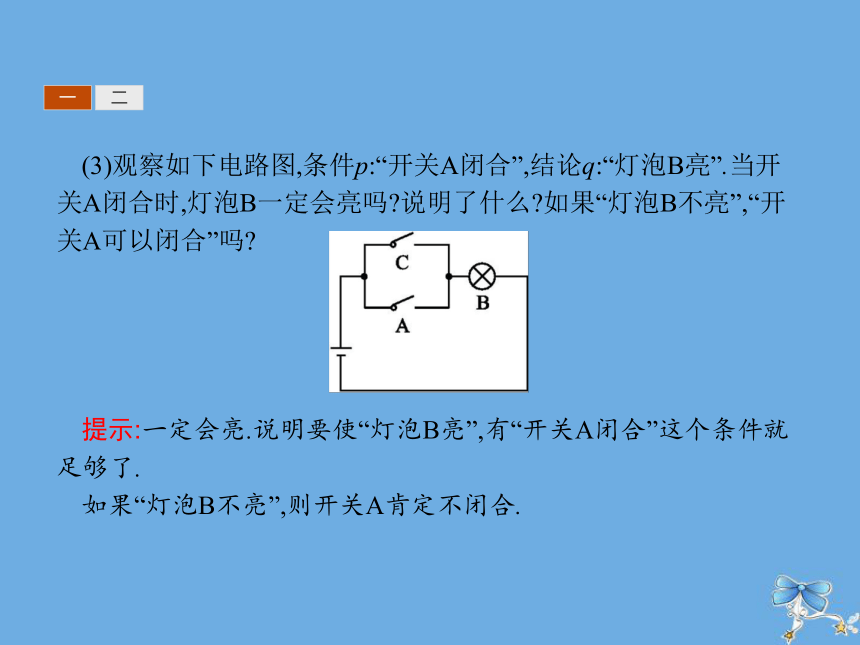
提示:说明由条件p不能推出结论q,记作p q.一二(3)观察如下电路图,条件p:“开关A闭合”,结论q:“灯泡B亮”.当开关A闭合时,灯泡B一定会亮吗?说明了什么?如果“灯泡B不亮”,“开关A可以闭合”吗?
提示:一定会亮.说明要使“灯泡B亮”,有“开关A闭合”这个条件就足够了.
如果“灯泡B不亮”,则开关A肯定不闭合.一二(4)下面电路中,条件p:“开关A闭合”成立,结论q:“灯泡B亮”成立吗?
提示:不成立.也就是说“若p,则q”为假命题.
2.填空
一般地,“若p则q”为真命题,就说p是q的充分条件,q是p的必要条件.
3.做一做
用“充分条件”和“必要条件”填空:
(1)若p:x=-3,q:x2=9,则p是q的 ,q是p的 .?
(2)若p:两个三角形面积相等,q:两个三角形全等,则p是q的 ,q是p的 .?
答案:(1)充分条件 必要条件 (2)必要条件 充分条件一二二、充要条件
1.(1)我们知道,当“x>1”成立时,能推出“x>0”.那么“x>0”的充分条件是否只能是“x>1”?
提示:不是.使结论“x>0”成立的条件并不唯一,如“x>1.2”,“3(2)由前面的知识,我们知道“x>0”是“x>1”的必要条件.那么“x>1”的必要条件是否只能是“x>0”?
提示:不是.例如“x>1”还能推出“x>-1”“x≥ ”等,这些都是“x>1”成立的必要条件.
(3)已知条件p:“三角形是等边三角形”,结论q:“三角形的三条边相等”,那么p是q的什么条件?q是p的什么条件?
提示:p?q,q?p.p是q的充分条件,q是p的充分条件,p是q的必要条件,q也是p的必要条件.一二(4)从命题“若p,则q”及其逆命题的真假角度,说一说p是q成立条件的所有情况.
提示:一二2.填空
如果“若p,则q”和它的逆命题“若q,则p”均是真命题,即既有p?q,又有q?p,就记作p?q.此时,p既是q的充分条件,也是q的必要条件,我们说p是q的充分必要条件,简称为充要条件.
3.做一做
实数a,b,c不全为0的一个充要条件是( )
A.实数a,b,c均不为0
B.实数a,b,c中至多有一个为0
C.实数a,b,c中至少有一个为0
D.实数a,b,c中至少有一个不为0
答案:D探究一探究二随堂演练探究一充分条件、必要条件及充要条件的判断
例1(1)对于任意的x,y∈R,“xy=0”是“x2+y2=0”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
(2)设四边形ABCD的两条对角线为AC,BD,则“四边形ABCD为菱形”是“AC⊥BD”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
(3)设A,B是两个集合,则“A∩B=A”是“A?B”的 ( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件探究一探究二随堂演练解析:(1)由x2+y2=0,得x=0且y=0,
由xy=0得x=0或y=0,即“xy=0” “x2+y2=0”.
(2)若“四边形ABCD为菱形”,显然对角线垂直;
但“AC⊥BD”推不出“四边形ABCD为菱形”,例如对角线垂直的等腰梯形.
所以“四边形ABCD为菱形”是“AC⊥BD”的充分不必要条件.
(3)∵A∩B=A?A?B,∴“A∩B=A”是“A?B”的充要条件.
答案:(1)A (2)A (3)C探究一探究二随堂演练延伸探究 例1(2)中,把原条件中的“四边形ABCD”改为“平行四边形ABCD”,其余不变,结论有变化吗?
解:若条件为平行四边形,则“ABCD为菱形”是“AC⊥BD”的充要条件.
变式训练1设A、B为两个互不相同的集合.命题p:x∈A∩B;命题q:x∈A或x∈B.则p是q的( )条件.
A.充分必要 B.充分不必要
C.必要不充分 D.既不充分又不必要
解析:若命题p:x∈A∩B成立,命题q:x∈A或x∈B一定成立;若命题q:x∈A或x∈B成立,但是x不一定是A∩B中的元素,所以p是q的充分不必要条件.
答案:B探究一探究二随堂演练探究二充要条件的证明
例2求证:关于x的一元二次不等式ax2-ax+1>0对于一切实数x都成立的充要条件是0分析:第一步,审题,分清条件与结论:“p是q的充要条件”中p是条件,q是结论;“p的充要条件是q”中,p是结论,q是条件.本题中条件是“00对一切实数x都成立”.
第二步,根据要求确定解题步骤.分别证明“充分性”与“必要性”,先证必要性:“结论?条件”;再证充分性:“条件?结论”.探究一探究二随堂演练探究一探究二随堂演练反思感悟 充要条件的证明
(1)充要条件的证明问题,关键是理清题意,认清条件与结论分别是什么.
(2)证明p是q的充要条件,既要证明“p?q”为真,又要证明“q?p”为真,前者证明的是充分性,后者证明的是必要性.
(3)证明p的充要条件是q,既要证明“p?q”为真,又要证明“q?p”为真,前者证明的是必要性,后者证明的是充分性.探究一探究二随堂演练变式训练2求证:方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0.
证明: (必要性)
∵关于x的方程ax2+bx+c=0有一个根为1,
∴x=1满足方程ax2+bx+c=0.
∴a×12+b×1+c=0,即a+b+c=0.
(充分性)
∵a+b+c=0,∴c=-a-b,代入方程ax2+bx+c=0中,可得ax2+bx-a-b=0,
即(x-1)(ax+a+b)=0.
因此,方程有一个根为x=1.故关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0.探究一探究二随堂演练1.“a=-3”是“|a|=3”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:A
2.“x>2”是“x>1”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:A探究一探究二随堂演练3.已知a,b是实数,则“a>0且b>0”是“a+b>0且ab>0”的 条件.?
解析:a>0且b>0?a+b>0且ab>0;a+b>0且ab>0?a>0且b>0,故为充要条件.
答案:充要探究一探究二随堂演练4.求证:一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
证明:充分性:
因为ac<0,
所以一元二次方程ax2+bx+c=0的判别式Δ=b2-4ac>0.
故一元二次方程一定有两个不相等实根,设为x1,x2,则x1x2= <0,
所以方程的两根异号.
即方程ax2+bx+c=0有一正根和一负根.
必要性:
一元二次方程有一正根和一负根,设为x1,x2,
则由根与系数的关系得x1x2= <0,即ac<0,
综上可知,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
1.(1)已知“若p,则q”为真命题,说明p与q之间有什么关系?
提示:说明当p成立时,一定能得出q成立.即由p通过推理可以得出q.这时我们就说,由p可以推出q,记作p?q.
(2)类似地,如果“若p,则q”为假命题,说明p与q之间有什么关系?
提示:说明由条件p不能推出结论q,记作p q.一二(3)观察如下电路图,条件p:“开关A闭合”,结论q:“灯泡B亮”.当开关A闭合时,灯泡B一定会亮吗?说明了什么?如果“灯泡B不亮”,“开关A可以闭合”吗?
提示:一定会亮.说明要使“灯泡B亮”,有“开关A闭合”这个条件就足够了.
如果“灯泡B不亮”,则开关A肯定不闭合.一二(4)下面电路中,条件p:“开关A闭合”成立,结论q:“灯泡B亮”成立吗?
提示:不成立.也就是说“若p,则q”为假命题.
2.填空
一般地,“若p则q”为真命题,就说p是q的充分条件,q是p的必要条件.
3.做一做
用“充分条件”和“必要条件”填空:
(1)若p:x=-3,q:x2=9,则p是q的 ,q是p的 .?
(2)若p:两个三角形面积相等,q:两个三角形全等,则p是q的 ,q是p的 .?
答案:(1)充分条件 必要条件 (2)必要条件 充分条件一二二、充要条件
1.(1)我们知道,当“x>1”成立时,能推出“x>0”.那么“x>0”的充分条件是否只能是“x>1”?
提示:不是.使结论“x>0”成立的条件并不唯一,如“x>1.2”,“3
提示:不是.例如“x>1”还能推出“x>-1”“x≥ ”等,这些都是“x>1”成立的必要条件.
(3)已知条件p:“三角形是等边三角形”,结论q:“三角形的三条边相等”,那么p是q的什么条件?q是p的什么条件?
提示:p?q,q?p.p是q的充分条件,q是p的充分条件,p是q的必要条件,q也是p的必要条件.一二(4)从命题“若p,则q”及其逆命题的真假角度,说一说p是q成立条件的所有情况.
提示:一二2.填空
如果“若p,则q”和它的逆命题“若q,则p”均是真命题,即既有p?q,又有q?p,就记作p?q.此时,p既是q的充分条件,也是q的必要条件,我们说p是q的充分必要条件,简称为充要条件.
3.做一做
实数a,b,c不全为0的一个充要条件是( )
A.实数a,b,c均不为0
B.实数a,b,c中至多有一个为0
C.实数a,b,c中至少有一个为0
D.实数a,b,c中至少有一个不为0
答案:D探究一探究二随堂演练探究一充分条件、必要条件及充要条件的判断
例1(1)对于任意的x,y∈R,“xy=0”是“x2+y2=0”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
(2)设四边形ABCD的两条对角线为AC,BD,则“四边形ABCD为菱形”是“AC⊥BD”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
(3)设A,B是两个集合,则“A∩B=A”是“A?B”的 ( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件探究一探究二随堂演练解析:(1)由x2+y2=0,得x=0且y=0,
由xy=0得x=0或y=0,即“xy=0” “x2+y2=0”.
(2)若“四边形ABCD为菱形”,显然对角线垂直;
但“AC⊥BD”推不出“四边形ABCD为菱形”,例如对角线垂直的等腰梯形.
所以“四边形ABCD为菱形”是“AC⊥BD”的充分不必要条件.
(3)∵A∩B=A?A?B,∴“A∩B=A”是“A?B”的充要条件.
答案:(1)A (2)A (3)C探究一探究二随堂演练延伸探究 例1(2)中,把原条件中的“四边形ABCD”改为“平行四边形ABCD”,其余不变,结论有变化吗?
解:若条件为平行四边形,则“ABCD为菱形”是“AC⊥BD”的充要条件.
变式训练1设A、B为两个互不相同的集合.命题p:x∈A∩B;命题q:x∈A或x∈B.则p是q的( )条件.
A.充分必要 B.充分不必要
C.必要不充分 D.既不充分又不必要
解析:若命题p:x∈A∩B成立,命题q:x∈A或x∈B一定成立;若命题q:x∈A或x∈B成立,但是x不一定是A∩B中的元素,所以p是q的充分不必要条件.
答案:B探究一探究二随堂演练探究二充要条件的证明
例2求证:关于x的一元二次不等式ax2-ax+1>0对于一切实数x都成立的充要条件是0
第二步,根据要求确定解题步骤.分别证明“充分性”与“必要性”,先证必要性:“结论?条件”;再证充分性:“条件?结论”.探究一探究二随堂演练探究一探究二随堂演练反思感悟 充要条件的证明
(1)充要条件的证明问题,关键是理清题意,认清条件与结论分别是什么.
(2)证明p是q的充要条件,既要证明“p?q”为真,又要证明“q?p”为真,前者证明的是充分性,后者证明的是必要性.
(3)证明p的充要条件是q,既要证明“p?q”为真,又要证明“q?p”为真,前者证明的是必要性,后者证明的是充分性.探究一探究二随堂演练变式训练2求证:方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0.
证明: (必要性)
∵关于x的方程ax2+bx+c=0有一个根为1,
∴x=1满足方程ax2+bx+c=0.
∴a×12+b×1+c=0,即a+b+c=0.
(充分性)
∵a+b+c=0,∴c=-a-b,代入方程ax2+bx+c=0中,可得ax2+bx-a-b=0,
即(x-1)(ax+a+b)=0.
因此,方程有一个根为x=1.故关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0.探究一探究二随堂演练1.“a=-3”是“|a|=3”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:A
2.“x>2”是“x>1”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:A探究一探究二随堂演练3.已知a,b是实数,则“a>0且b>0”是“a+b>0且ab>0”的 条件.?
解析:a>0且b>0?a+b>0且ab>0;a+b>0且ab>0?a>0且b>0,故为充要条件.
答案:充要探究一探究二随堂演练4.求证:一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
证明:充分性:
因为ac<0,
所以一元二次方程ax2+bx+c=0的判别式Δ=b2-4ac>0.
故一元二次方程一定有两个不相等实根,设为x1,x2,则x1x2= <0,
所以方程的两根异号.
即方程ax2+bx+c=0有一正根和一负根.
必要性:
一元二次方程有一正根和一负根,设为x1,x2,
则由根与系数的关系得x1x2= <0,即ac<0,
综上可知,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
