人教版数学初中七年级下册知识讲解,巩固练习(教学资料,补习资料):专题5.3 平行线的性质(含答案)
文档属性
| 名称 | 人教版数学初中七年级下册知识讲解,巩固练习(教学资料,补习资料):专题5.3 平行线的性质(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 402.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-26 12:10:56 | ||
图片预览




文档简介
第五章 相交线与平行线
5.3 平行线的性质
知识
1.平行线的性质
(1)两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角__________.
符号语言为:如果a∥b,那么∠1=∠2,示意图如图:
(2)两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角__________.
符号语言为:如果a∥b,那么∠2=∠4,示意图如图:
(3)两条平行线被第三条直线所截,同旁内角互补,简单说成:两直线平行,同旁内角__________.
符号语言为:如果a∥b,那么∠2+∠3=180°.示意图如图:
2.命题
(1)定义:判断一件事情的语句,叫做__________,如:对顶角相等.
(2)组成:命题由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,通常写成:“如果……那么……”的形式,这时“如果”后接的部分是题设,“那么”后接的部分是结论.
(3)真命题:如果题设成立,那么结论一定成立的命题.
(4)假命题:命题中题设成立时,不能保证结论一定成立的命题.
3.定理与证明
(1)定理:经过推理证实的真命题叫做__________,定理也可以作为继续推理的依据.
(2)证明:在很多情况下,一个命题的正确性需要经过推理才能作出判断,这个推理过程叫做_________.
知识参考答案:
1.(1)相等(2)相等(3)互补
2.(1)命题
3.(1)定理(2)证明
重点
重点
平行线的性质的探索及对性质的理解;掌握命题、定理的概念,了解证明的意义
难点
平行线性质的应用;分清命题的组成,说出一个命题是真命题还是假命题
易错
忽视两直线平行的条件;命题改写不正确
一、平行线的性质
只有在“两条平行线被第三条直线所截”的前提下才存在同位角相等、内错角相等、同旁内角互补的结论,这是平行线特有的性质.
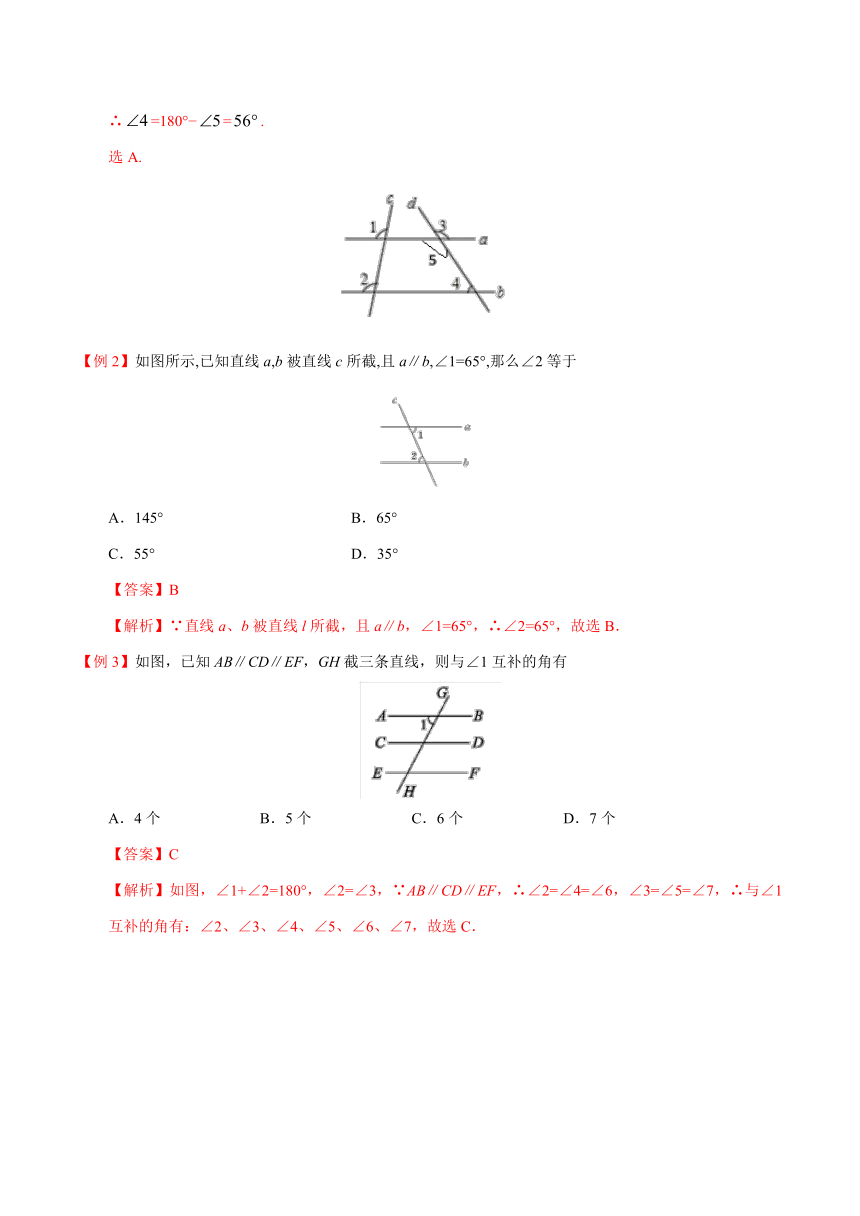
【例1】如图所示,直线、、、的位置如图所示,若,,,则的度数为
A. B.
C. D.
【答案】A
【解析】∵,
∴∥,
∵,∴,
∴=180°?=.
选A.
【例2】如图所示,已知直线a,b被直线c所截,且a∥b,∠1=65°,那么∠2等于
A.145° B.65°
C.55° D.35°
【答案】B
【解析】∵直线a、b被直线l所截,且a∥b,∠1=65°,∴∠2=65°,故选B.
【例3】如图,已知AB∥CD∥EF,GH截三条直线,则与∠1互补的角有
A.4个 B.5个 C.6个 D.7个
【答案】C
【解析】如图,∠1+∠2=180°,∠2=∠3,∵AB∥CD∥EF,∴∠2=∠4=∠6,∠3=∠5=∠7,∴与∠1互补的角有:∠2、∠3、∠4、∠5、∠6、∠7,故选C.
二、命题
判断一个命题是假命题,只需举出一个反例(符合命题的题设,不满足命题的结论)即可,而说明一个命题是真命题需要从已知出发,经过一步步推理,最后得出正确结论.
【例4】下列语句:①三角形的内角和是180°;②作一个角等于一个已知角;③两条直线被第三条直线所截,同位角相等;④延长线段AB到C,使BC=AB,其中是命题的有
A.①② B.②③ C.①④ D.①③
【答案】D
【解析】①三角形的内角和是180°,是命题;②作一个角等于一个已知角,不是命题;③两条直线被第三条直线所截,同位角相等,是命题;④延长线段AB到C,使BC=AB,不是命题,故选D.
【例5】下列语句中,假命题的是
A.一条直线有且只有一条垂线 B.不相等的两个角一定不是对顶角,
C.直角的补角必是直角 D.两直线平行,同旁内角互补
【答案】A
【解析】A、一条直线有且只有一条垂线是假命题;
B、不相等的两个角一定不是对顶角是真命题;
C、直角的补角必是直角是真命题;
D、两直线平行,同旁内角互补是真命题,
故选A.
【例6】下列命题中,是真命题的是
A.互补的角是邻补角 B.相等的角是对顶角
C.内错角相等 D.对顶角都相等
【答案】D
【解析】A、两直线平行时,同旁内角互补,此时这一对同旁内角不是邻补角,故本选项错误;
B、等腰三角形的两个底角相等,此时这两个底角不是对顶角,故本选项错误;
C、只有两直线平行时,内错角才相等,故本选项错误;? D、对顶角都相等,故本选项正确.?
故选D.
三、定理与证明
证明中的每一步推理都要有根据,不能“想当然”,这些根据,可以是已知条件,也可以是学过的定义、基本事实、定理等.
【例7】如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截.在下面三个条件中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.①AB⊥BC,CD⊥BC,②BE∥CF,③∠1=∠2.
【解析】已知:如图,AB⊥BC,CD⊥BC,BE∥CF.求证:∠1=∠2.
证明:∵AB⊥BC,CD⊥BC,
∴∠ABC=∠DCB,
又∵BE∥CF,
∴∠EBC=∠FCB,
∴∠ABC?∠EBC=∠DCB?∠FCB,
∴∠1=∠2.
四、平行线性质与判定的综合应用
平行线的性质描述的是“数量关系”,它的前提是两直线平行,然后得出角相等或互补的关系,是由“位置关系”到“数量关系”;平行线的判定是以角的相等或互补为前提,推导出两直线平行,是从“数量关系”到“位置关系”.
【例8】如图,∠1+∠2=180°,∠B=∠E,试猜想AB与CE之间有怎样的位置关系?并说明理由.
【解析】AB∥CE,理由如下:
∵∠1+∠2=180°,
∴DE∥BC(同旁内角互补,两直线平行),
∴∠ADF=∠B(两直线平行,同位角相等),
∵∠B=∠E,
∴∠ADF=∠E,
∴AB∥CE(内错角相等,两直线平行).
基础训练
1.如图,若,则下列结论一定成立的是
A. B.
C. D.
2.如图,将三角板的直角顶点放在直尺的一边上,若,则的度数为
A. B. C. D.
3.下列语句不是命题的是
A.明天有可能下雨 B.同位角相等
C.∠A是锐角 D.中国是世界上人口最多的国家
4.如图所示,AB⊥EF,CD⊥EF,∠1=∠F=40°,且A,C,F三点共线,那么与∠FCD相等的角有
A.1个 B.2个
C.3个 D.4个
5.如图,BE平分∠ABC,DE∥BC,图中相等的角共有
A.3对 B.4对
C.5对 D.6对
6.如图,AB∥CD,若∠2是∠1的4倍,则∠2的度数是
A.144° B.135° C.126° D.108°
7.如图,AB∥CD,直线l分别交AB、CD于E,F,∠1=56°,则∠2的度数是________°.
8.如图,a∥b,AC分别交直线a、b于点B、C,,若,则__________度.
9.如图,AB∥CD,∠B=115°,∠C=45°,则∠BEC=__________.
10.分别把下列命题写成“如果……,那么……”的形式.
(1)两点确定一条直线;
(2)等角的补角相等;
(3)内错角相等.
11.如图,于,交于点,交于点,,,试判断和的位置关系,并说明理由.
能力测试
12.如图,已知AB∥CD∥EF,则∠x、∠y、∠z三者之间的关系是
A. B.
C. D.
13.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是__________.
14.如图,一条公路两次转弯后又回到原来的方向.若第一次转弯时∠B=140°,则∠C的度数是______________.
15.如图,点E在AB上,CE,DE分别平分∠BCD,∠ADC,∠1+∠2=90°,∠B=75°,求∠A的度数.
真题练习
16.(2018·甘孜州)如图,已知DE∥BC,如果∠1=70°,那么∠B的度数为
A.70° B.100°
C.110° D.120°
17.(2018·赤峰市)已知,直线EF分别交AB、CD于点G、H,∠EGB=25°,将一个60°角的直角三角尺如图放置(60°角的顶点与H重合),则∠PHG等于
A.30° B.35°
C.40° D.45°
18.(2018·绵阳市)如图,有一块含有30°角的直角三角形板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是
A.14° B.15°
C.16° D.17°
19.(2018·海南)将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为
A.10° B.15°
C.20° D.25°
20.(2018·韶关市)如图,,则,,则的大小是
A. B.
C. D.
21.(2018·泸州市)如图,直线a∥b,直线分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=50°,则∠2的度数是
A.50° B.70°
C.80° D.110°
22.(2018·枣庄市)已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为
A.20° B.30°
C.45° D.50°
23.(2018·齐齐哈尔市)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为
A.10° B.15°
C.18° D.30°
24.(2018·南通市)如图,∠AOB=40°,OP平分∠AOB,点C为射线OP上一点,作CD⊥OA于点D,在∠POB的内部作CE∥OB,则∠DCE=___________度.
25.(2018·柳州市)如图,,若,则___________.
参考答案
1.【答案】D
【解析】因为∠1=∠3,所以AD∥BC,所以∠1+∠2=180°,故选D.
2.【答案】C
【解析】如图,因为AD∥BC,所以∠1=∠3=65°,因为∠2+∠3+90°=180°,所以∠2=90°-∠3=90°-65°=25°,故选C.
3.【答案】A
【解析】A、明天有可能下雨,不是判断语句,故不是命题,符合题意;
B、同位角相等是命题,故不符合题意;
C、∠A是锐角是命题,故不符合题意;
D、中国是世界上人口最多的国家是命题,故不符合题意,
故选A.
5.【答案】C
【解析】∵DE∥BC,∴∠DEB=∠EBC,∠ADE=∠ABC,∠AED=∠ACB,又∵BE平分∠ABC,∴∠ABE=∠EBC,即∠ABE=∠DEB,所以图中相等的角共有5对,故选C.
6.【答案】A
【解析】如图,∵AB∥CD,∴∠1+∠3=180°,∵∠2=∠3=4∠1,∴∠1+4∠1=180°,即∠1=36°,则∠2=
4∠1=144°,故选A.
7.【答案】124
【解析】∵∠1=56°, ∴∠3=180°?∠1=124°, ∵AB∥CD, ∴∠2=∠3=124°. 故答案为:124.
8.【答案】65
【解析】∵AC⊥DC,∴∠1+∠3=90°,∵∠1=25°,∴∠3=90°-∠1=90°-25°=65°,∵a∥b,∴∠2=∠1=65°,故答案为:65.
9.【答案】110°
【解析】如图,过点E作EF∥AB.因为AB∥CD,所以EF∥CD,所以∠B+∠BEF=180°,∠C=∠CEF.
因为∠B=115°,∠C=45°,所以∠BEF=180°-115°=65°,∠CEF=45°,所以∠BEC=∠BEF+∠CEF=65°+45°=
110°,故答案为:110°.
10.【解析】(1)如果有两个定点,那么过这两点有且只有一条直线.
(2)如果两个角分别是两个等角的补角,那么这两个角相等.
(3)如果两个角是内错角,那么这两个角相等.
11.【解析】如图,过点作.
∵,∴(两直线平行,同位角相等).
∵(已知),∴(等量代换).
∵(已知),∴(垂直的定义),
∴.
∵,∴,
∴(同旁内角互补,两直线平行),
∴(平行于同一条直线的两条直线互相平行).
14.【答案】140°
【解析】∵AB∥CD,∠B=140°, ∴∠C=∠B=140°. 故答案是:140°.
15.【答案】105°
【解析】∵∠1+∠2=90°,CE,DE分别平分∠BCD,∠ADC,
∴∠ADC+∠BCD=2(∠1+∠2)=180°,
∴AD∥BC,∴∠A+∠B=180°,
∵∠B=75°,
∴∠A=180°﹣75°=105°.
16.【答案】C
【解析】如图,∵DE∥BC,
∴∠2+∠B=180°,
∵∠2=∠1=70°,
∴∠B=180°?70°=110°,
故选C.
17.【答案】B
【解析】∵AB∥CD,∴∠EHD=∠EGB=25°.
又∵∠PHD=60°,∴∠PHG=60°﹣25°=35°.
故选B.
18.【答案】C
【解析】如图,
∵∠ABC=60°,∠2=44°,
∴∠EBC=16°,
∵BE∥CD,
∴∠1=∠EBC=16°,
故选C.
20.【答案】B
【解析】∵∠DEC=100°,∠C=40°,
∴∠D=180°?∠DEC?∠C=40°,
又∵AB∥CD,
∴∠B=∠D=40°,
故选B.
21.【答案】C
【解析】因为a∥b,
所以∠1=∠BAD=50°,
因为AD是∠BAC的平分线,
所以∠BAC=2∠BAD=100°,
所以∠2=180°?∠BAC=180°?100°=80°.
故选C.
22.【答案】D
【解析】因为m∥n,所以∠2=∠1+30°,所以∠2=30°+20°=50°,故选D.
23.【答案】B
【解析】由题意可得:∠EDF=45°,∠ABC=30°,
∵AB∥CF,
∴∠ABD=∠EDF=45°,
∴∠DBC=45°﹣30°=15°.
故选:B.
5.3 平行线的性质
知识
1.平行线的性质
(1)两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角__________.
符号语言为:如果a∥b,那么∠1=∠2,示意图如图:
(2)两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角__________.
符号语言为:如果a∥b,那么∠2=∠4,示意图如图:
(3)两条平行线被第三条直线所截,同旁内角互补,简单说成:两直线平行,同旁内角__________.
符号语言为:如果a∥b,那么∠2+∠3=180°.示意图如图:
2.命题
(1)定义:判断一件事情的语句,叫做__________,如:对顶角相等.
(2)组成:命题由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,通常写成:“如果……那么……”的形式,这时“如果”后接的部分是题设,“那么”后接的部分是结论.
(3)真命题:如果题设成立,那么结论一定成立的命题.
(4)假命题:命题中题设成立时,不能保证结论一定成立的命题.
3.定理与证明
(1)定理:经过推理证实的真命题叫做__________,定理也可以作为继续推理的依据.
(2)证明:在很多情况下,一个命题的正确性需要经过推理才能作出判断,这个推理过程叫做_________.
知识参考答案:
1.(1)相等(2)相等(3)互补
2.(1)命题
3.(1)定理(2)证明
重点
重点
平行线的性质的探索及对性质的理解;掌握命题、定理的概念,了解证明的意义
难点
平行线性质的应用;分清命题的组成,说出一个命题是真命题还是假命题
易错
忽视两直线平行的条件;命题改写不正确
一、平行线的性质
只有在“两条平行线被第三条直线所截”的前提下才存在同位角相等、内错角相等、同旁内角互补的结论,这是平行线特有的性质.
【例1】如图所示,直线、、、的位置如图所示,若,,,则的度数为
A. B.
C. D.
【答案】A
【解析】∵,
∴∥,
∵,∴,
∴=180°?=.
选A.
【例2】如图所示,已知直线a,b被直线c所截,且a∥b,∠1=65°,那么∠2等于
A.145° B.65°
C.55° D.35°
【答案】B
【解析】∵直线a、b被直线l所截,且a∥b,∠1=65°,∴∠2=65°,故选B.
【例3】如图,已知AB∥CD∥EF,GH截三条直线,则与∠1互补的角有
A.4个 B.5个 C.6个 D.7个
【答案】C
【解析】如图,∠1+∠2=180°,∠2=∠3,∵AB∥CD∥EF,∴∠2=∠4=∠6,∠3=∠5=∠7,∴与∠1互补的角有:∠2、∠3、∠4、∠5、∠6、∠7,故选C.
二、命题
判断一个命题是假命题,只需举出一个反例(符合命题的题设,不满足命题的结论)即可,而说明一个命题是真命题需要从已知出发,经过一步步推理,最后得出正确结论.
【例4】下列语句:①三角形的内角和是180°;②作一个角等于一个已知角;③两条直线被第三条直线所截,同位角相等;④延长线段AB到C,使BC=AB,其中是命题的有
A.①② B.②③ C.①④ D.①③
【答案】D
【解析】①三角形的内角和是180°,是命题;②作一个角等于一个已知角,不是命题;③两条直线被第三条直线所截,同位角相等,是命题;④延长线段AB到C,使BC=AB,不是命题,故选D.
【例5】下列语句中,假命题的是
A.一条直线有且只有一条垂线 B.不相等的两个角一定不是对顶角,
C.直角的补角必是直角 D.两直线平行,同旁内角互补
【答案】A
【解析】A、一条直线有且只有一条垂线是假命题;
B、不相等的两个角一定不是对顶角是真命题;
C、直角的补角必是直角是真命题;
D、两直线平行,同旁内角互补是真命题,
故选A.
【例6】下列命题中,是真命题的是
A.互补的角是邻补角 B.相等的角是对顶角
C.内错角相等 D.对顶角都相等
【答案】D
【解析】A、两直线平行时,同旁内角互补,此时这一对同旁内角不是邻补角,故本选项错误;
B、等腰三角形的两个底角相等,此时这两个底角不是对顶角,故本选项错误;
C、只有两直线平行时,内错角才相等,故本选项错误;? D、对顶角都相等,故本选项正确.?
故选D.
三、定理与证明
证明中的每一步推理都要有根据,不能“想当然”,这些根据,可以是已知条件,也可以是学过的定义、基本事实、定理等.
【例7】如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截.在下面三个条件中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.①AB⊥BC,CD⊥BC,②BE∥CF,③∠1=∠2.
【解析】已知:如图,AB⊥BC,CD⊥BC,BE∥CF.求证:∠1=∠2.
证明:∵AB⊥BC,CD⊥BC,
∴∠ABC=∠DCB,
又∵BE∥CF,
∴∠EBC=∠FCB,
∴∠ABC?∠EBC=∠DCB?∠FCB,
∴∠1=∠2.
四、平行线性质与判定的综合应用
平行线的性质描述的是“数量关系”,它的前提是两直线平行,然后得出角相等或互补的关系,是由“位置关系”到“数量关系”;平行线的判定是以角的相等或互补为前提,推导出两直线平行,是从“数量关系”到“位置关系”.
【例8】如图,∠1+∠2=180°,∠B=∠E,试猜想AB与CE之间有怎样的位置关系?并说明理由.
【解析】AB∥CE,理由如下:
∵∠1+∠2=180°,
∴DE∥BC(同旁内角互补,两直线平行),
∴∠ADF=∠B(两直线平行,同位角相等),
∵∠B=∠E,
∴∠ADF=∠E,
∴AB∥CE(内错角相等,两直线平行).
基础训练
1.如图,若,则下列结论一定成立的是
A. B.
C. D.
2.如图,将三角板的直角顶点放在直尺的一边上,若,则的度数为
A. B. C. D.
3.下列语句不是命题的是
A.明天有可能下雨 B.同位角相等
C.∠A是锐角 D.中国是世界上人口最多的国家
4.如图所示,AB⊥EF,CD⊥EF,∠1=∠F=40°,且A,C,F三点共线,那么与∠FCD相等的角有
A.1个 B.2个
C.3个 D.4个
5.如图,BE平分∠ABC,DE∥BC,图中相等的角共有
A.3对 B.4对
C.5对 D.6对
6.如图,AB∥CD,若∠2是∠1的4倍,则∠2的度数是
A.144° B.135° C.126° D.108°
7.如图,AB∥CD,直线l分别交AB、CD于E,F,∠1=56°,则∠2的度数是________°.
8.如图,a∥b,AC分别交直线a、b于点B、C,,若,则__________度.
9.如图,AB∥CD,∠B=115°,∠C=45°,则∠BEC=__________.
10.分别把下列命题写成“如果……,那么……”的形式.
(1)两点确定一条直线;
(2)等角的补角相等;
(3)内错角相等.
11.如图,于,交于点,交于点,,,试判断和的位置关系,并说明理由.
能力测试
12.如图,已知AB∥CD∥EF,则∠x、∠y、∠z三者之间的关系是
A. B.
C. D.
13.如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是__________.
14.如图,一条公路两次转弯后又回到原来的方向.若第一次转弯时∠B=140°,则∠C的度数是______________.
15.如图,点E在AB上,CE,DE分别平分∠BCD,∠ADC,∠1+∠2=90°,∠B=75°,求∠A的度数.
真题练习
16.(2018·甘孜州)如图,已知DE∥BC,如果∠1=70°,那么∠B的度数为
A.70° B.100°
C.110° D.120°
17.(2018·赤峰市)已知,直线EF分别交AB、CD于点G、H,∠EGB=25°,将一个60°角的直角三角尺如图放置(60°角的顶点与H重合),则∠PHG等于
A.30° B.35°
C.40° D.45°
18.(2018·绵阳市)如图,有一块含有30°角的直角三角形板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是
A.14° B.15°
C.16° D.17°
19.(2018·海南)将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为
A.10° B.15°
C.20° D.25°
20.(2018·韶关市)如图,,则,,则的大小是
A. B.
C. D.
21.(2018·泸州市)如图,直线a∥b,直线分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=50°,则∠2的度数是
A.50° B.70°
C.80° D.110°
22.(2018·枣庄市)已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为
A.20° B.30°
C.45° D.50°
23.(2018·齐齐哈尔市)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为
A.10° B.15°
C.18° D.30°
24.(2018·南通市)如图,∠AOB=40°,OP平分∠AOB,点C为射线OP上一点,作CD⊥OA于点D,在∠POB的内部作CE∥OB,则∠DCE=___________度.
25.(2018·柳州市)如图,,若,则___________.
参考答案
1.【答案】D
【解析】因为∠1=∠3,所以AD∥BC,所以∠1+∠2=180°,故选D.
2.【答案】C
【解析】如图,因为AD∥BC,所以∠1=∠3=65°,因为∠2+∠3+90°=180°,所以∠2=90°-∠3=90°-65°=25°,故选C.
3.【答案】A
【解析】A、明天有可能下雨,不是判断语句,故不是命题,符合题意;
B、同位角相等是命题,故不符合题意;
C、∠A是锐角是命题,故不符合题意;
D、中国是世界上人口最多的国家是命题,故不符合题意,
故选A.
5.【答案】C
【解析】∵DE∥BC,∴∠DEB=∠EBC,∠ADE=∠ABC,∠AED=∠ACB,又∵BE平分∠ABC,∴∠ABE=∠EBC,即∠ABE=∠DEB,所以图中相等的角共有5对,故选C.
6.【答案】A
【解析】如图,∵AB∥CD,∴∠1+∠3=180°,∵∠2=∠3=4∠1,∴∠1+4∠1=180°,即∠1=36°,则∠2=
4∠1=144°,故选A.
7.【答案】124
【解析】∵∠1=56°, ∴∠3=180°?∠1=124°, ∵AB∥CD, ∴∠2=∠3=124°. 故答案为:124.
8.【答案】65
【解析】∵AC⊥DC,∴∠1+∠3=90°,∵∠1=25°,∴∠3=90°-∠1=90°-25°=65°,∵a∥b,∴∠2=∠1=65°,故答案为:65.
9.【答案】110°
【解析】如图,过点E作EF∥AB.因为AB∥CD,所以EF∥CD,所以∠B+∠BEF=180°,∠C=∠CEF.
因为∠B=115°,∠C=45°,所以∠BEF=180°-115°=65°,∠CEF=45°,所以∠BEC=∠BEF+∠CEF=65°+45°=
110°,故答案为:110°.
10.【解析】(1)如果有两个定点,那么过这两点有且只有一条直线.
(2)如果两个角分别是两个等角的补角,那么这两个角相等.
(3)如果两个角是内错角,那么这两个角相等.
11.【解析】如图,过点作.
∵,∴(两直线平行,同位角相等).
∵(已知),∴(等量代换).
∵(已知),∴(垂直的定义),
∴.
∵,∴,
∴(同旁内角互补,两直线平行),
∴(平行于同一条直线的两条直线互相平行).
14.【答案】140°
【解析】∵AB∥CD,∠B=140°, ∴∠C=∠B=140°. 故答案是:140°.
15.【答案】105°
【解析】∵∠1+∠2=90°,CE,DE分别平分∠BCD,∠ADC,
∴∠ADC+∠BCD=2(∠1+∠2)=180°,
∴AD∥BC,∴∠A+∠B=180°,
∵∠B=75°,
∴∠A=180°﹣75°=105°.
16.【答案】C
【解析】如图,∵DE∥BC,
∴∠2+∠B=180°,
∵∠2=∠1=70°,
∴∠B=180°?70°=110°,
故选C.
17.【答案】B
【解析】∵AB∥CD,∴∠EHD=∠EGB=25°.
又∵∠PHD=60°,∴∠PHG=60°﹣25°=35°.
故选B.
18.【答案】C
【解析】如图,
∵∠ABC=60°,∠2=44°,
∴∠EBC=16°,
∵BE∥CD,
∴∠1=∠EBC=16°,
故选C.
20.【答案】B
【解析】∵∠DEC=100°,∠C=40°,
∴∠D=180°?∠DEC?∠C=40°,
又∵AB∥CD,
∴∠B=∠D=40°,
故选B.
21.【答案】C
【解析】因为a∥b,
所以∠1=∠BAD=50°,
因为AD是∠BAC的平分线,
所以∠BAC=2∠BAD=100°,
所以∠2=180°?∠BAC=180°?100°=80°.
故选C.
22.【答案】D
【解析】因为m∥n,所以∠2=∠1+30°,所以∠2=30°+20°=50°,故选D.
23.【答案】B
【解析】由题意可得:∠EDF=45°,∠ABC=30°,
∵AB∥CF,
∴∠ABD=∠EDF=45°,
∴∠DBC=45°﹣30°=15°.
故选:B.
