人教版数学初中七年级下册知识讲解,巩固练习(教学资料,补习资料):专题5.4 平移(含答案)
文档属性
| 名称 | 人教版数学初中七年级下册知识讲解,巩固练习(教学资料,补习资料):专题5.4 平移(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 369.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-26 12:12:35 | ||
图片预览


文档简介
第五章 相交线与平行线
5.4 平移
知识
1.平移的定义
(1)定义:把一个图形整体沿某一直线方向移动,会得到一个新的图形,图形的这种移动,叫做________.
(2)要素:一是平移的_________,二是平移的距离.
2.平移的性质
性质:平移后的新图形与原图形的形状和大小完全__________,即平移前后的两个图形的对应边__________(或在同一条直线上)且相等,对应角相等;连接各组对应点的线段平行(或在同一条直线上)且相等.
【注意】(1)连接对应点的线段的长度就是平移的距离.
(2)从原图形上一点到其对应点的方向即为平移的方向.
知识参考答案:
1.(1)平移(2)方向 2.相同,平行
重点
重点
平移的概念及其性质;利用平移作图
难点
探索平移的性质
易错
把握不准平移的方向和距离出错
一、平移的定义
把一个图形整体沿着某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
【例1】下列现象中,不属于平移的是
A.滑雪运动员在的平坦雪地上滑行 B.大楼上上下下地迎送来客的电梯
C.钟摆的摆动 D.火车在笔直的铁轨上飞驰而过
【答案】C
【解析】A.滑雪运动员在平坦的雪地上滑行,符合平移的定义,故不符合题意;
B.大楼电梯上上下下地迎送来客,是平移,故不符合题意;
C.钟摆的摆动不是平移,故符合题意;
D.火车在笔直的铁轨上飞驰而过,是平移,故不符合题意;
故答案为C.
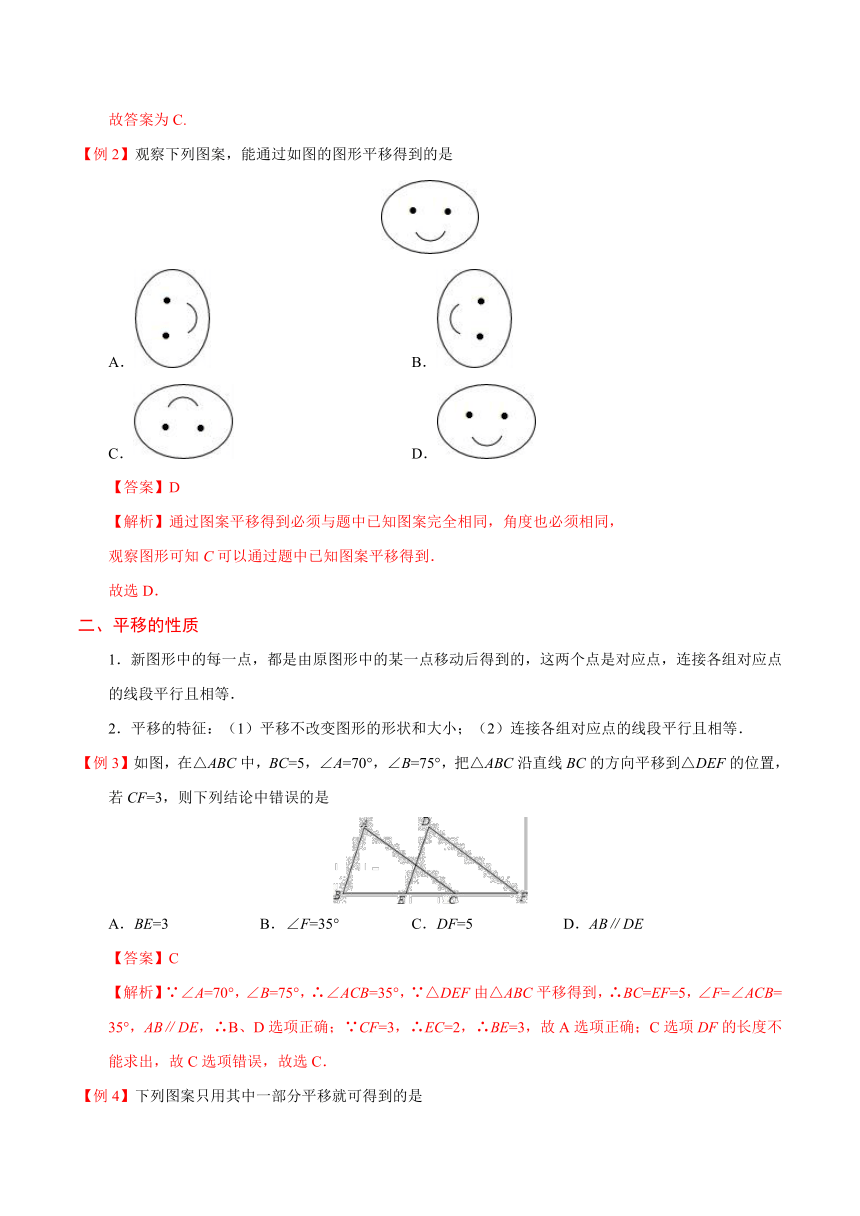
【例2】观察下列图案,能通过如图的图形平移得到的是
A. B.
C. D.
【答案】D
【解析】通过图案平移得到必须与题中已知图案完全相同,角度也必须相同,
观察图形可知C可以通过题中已知图案平移得到.
故选D.
二、平移的性质
1.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行且相等.
2.平移的特征:(1)平移不改变图形的形状和大小;(2)连接各组对应点的线段平行且相等.
【例3】如图,在△ABC中,BC=5,∠A=70°,∠B=75°,把△ABC沿直线BC的方向平移到△DEF的位置,若CF=3,则下列结论中错误的是
A.BE=3 B.∠F=35° C.DF=5 D.AB∥DE
【答案】C
【解析】∵∠A=70°,∠B=75°,∴∠ACB=35°,∵△DEF由△ABC平移得到,∴BC=EF=5,∠F=∠ACB=
35°,AB∥DE,∴B、D选项正确;∵CF=3,∴EC=2,∴BE=3,故A选项正确;C选项DF的长度不能求出,故C选项错误,故选C.
【例4】下列图案只用其中一部分平移就可得到的是
A. B.
C. D.
【答案】B
【解析】A、通过平移得不到,故错误;
B、图形的形状和大小不变,符合平移性质,故正确;
C、通过平移得不到,故错误;
D、最后一个形状不同,故错误.
故选B.
三、平移的应用
在解决面积问题时,如果图形是不规则图形或者是由几个图形组成的,可设法将图形转化为规则的图形求面积,平移可作为其中的一种手段.
【例5】若在运动会颁奖台上面及两侧铺上地毯(如图阴影部分),长为m,宽为n,高为h,(单位为:cm).
(1)用m,n,h表示需要地毯的面积;
(2)若m=160,n=60,h=80,求地毯的面积.
【答案】(1)mn+2nh;(2)19200 cm2
【解析】(1)地毯的面积为:(m+2h)n=mn+2nh.
(2)地毯总长:80×2+160=320(cm),
320×60=19200(cm2),
答:地毯的面积为19200 cm2.
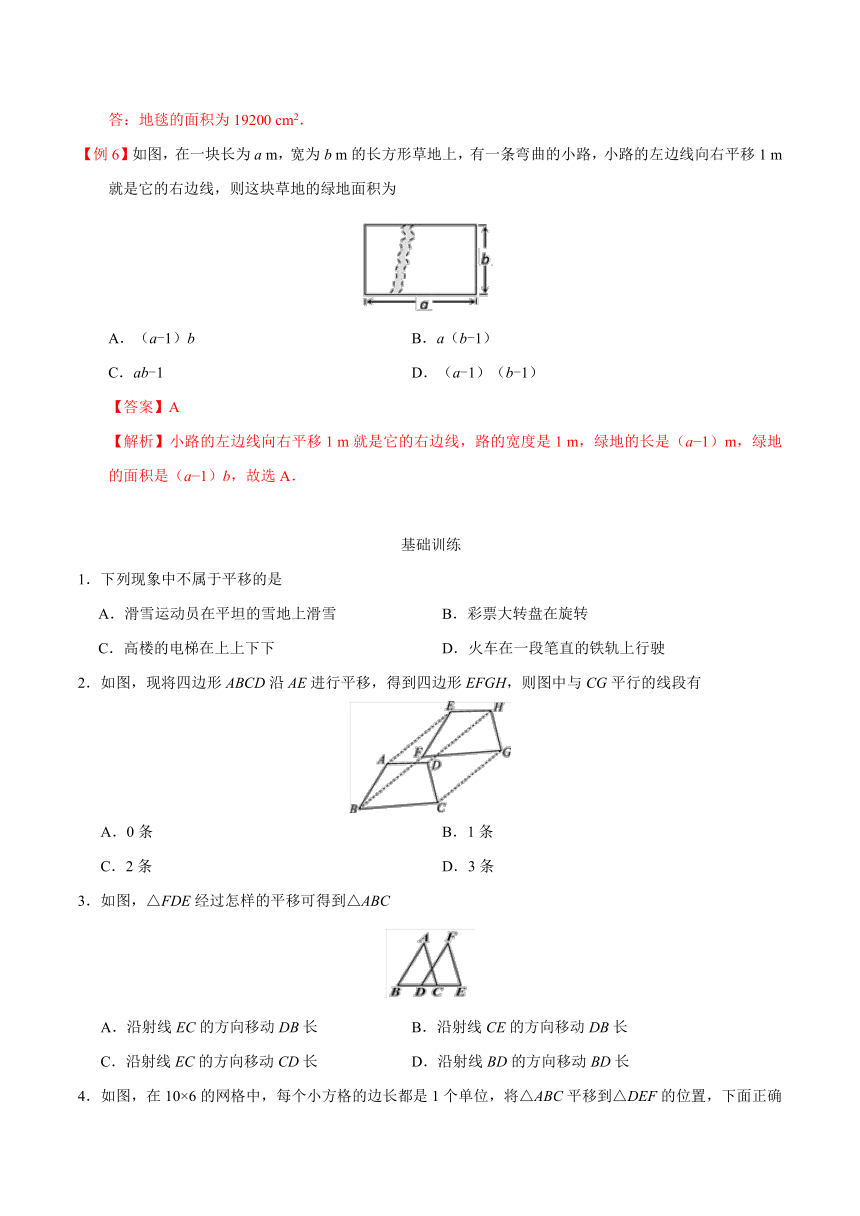
【例6】如图,在一块长为a m,宽为b m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1 m就是它的右边线,则这块草地的绿地面积为
A.(a-1)b B.a(b-1)
C.ab-1 D.(a-1)(b-1)
【答案】A
【解析】小路的左边线向右平移1 m就是它的右边线,路的宽度是1 m,绿地的长是(a?1)m,绿地的面积是(a?1)b,故选A.
基础训练
1.下列现象中不属于平移的是
A.滑雪运动员在平坦的雪地上滑雪 B.彩票大转盘在旋转
C.高楼的电梯在上上下下 D.火车在一段笔直的铁轨上行驶
2.如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有
A.0条 B.1条
C.2条 D.3条
3.如图,△FDE经过怎样的平移可得到△ABC
A.沿射线EC的方向移动DB长 B.沿射线CE的方向移动DB长
C.沿射线EC的方向移动CD长 D.沿射线BD的方向移动BD长
4.如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是
A.先向左平移5个单位,再向下平移2个单位
B.先向右平移5个单位,再向下平移2个单位
C.先向左平移5个单位,再向上平移2个单位
D.先向右平移5个单位,再向下平移2个单位
5.如图,将△ABE向右平移得到△DCF,与交于点,其中,,则
A. B. C. D.
6.如图,将△ABE向右平移2 cm得到△DCF,如果△ABE的周长是16 cm,那么四边形ABFD的周长是
A.16 cm B.18 cm C.20 cm D.21 cm
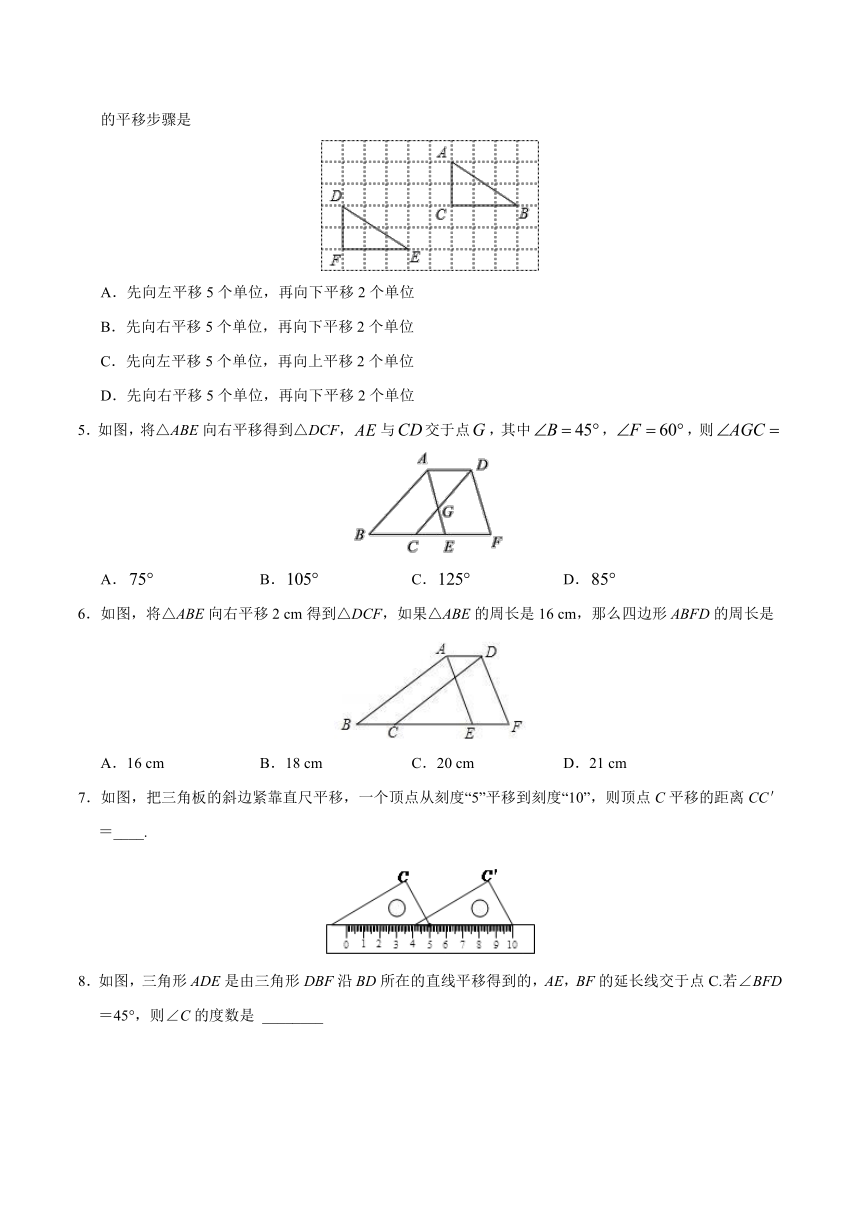
7.如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC'=____.
8.如图,三角形ADE是由三角形DBF沿BD所在的直线平移得到的,AE,BF的延长线交于点C.若∠BFD=45°,则∠C的度数是 ________
9.如图, 是ABC向右平移4 cm得到的,已知∠ACB=30°,B′C=3 cm,则∠C′=_________,B′C′=________cm.
10.要在台阶上铺设某种红地毯,已知这种红地毯每平方米的售价是40元,台阶宽为3米,侧面如图所示.购买这种红地毯至少需要__________元.
11.如图,△ABC沿直线BC向右移了3 cm,得△FDE,且BC=6 cm,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
12.如图,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F的位置,并作出△DEF.
13.如图,在三角形ABC中,已知AB=3cm,AC=4cm,BC=5cm.现将三角形ABC沿着垂直于BC的方向平移6cm,到三角形DEF的位置,求三角形ABC所扫过的面积.
能力测试
14.如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中已有的线段走,那么从A点到B点的最短距离的走法共有
A.1种 B.2种
C.3种 D.4种
15.多边形的相邻两边互相垂直,则这个多边形的周长为
A.a+b B.2a+b
C.2a+2b D.2b+a
16.如图,平移ABC可得到DEF,如果∠C=60°,AE=7cm,AB=4cm,那么∠F= ______ 度,DB= ______ cm.
17.如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种红色地毯的售价为每平方米32元,主楼梯宽为2 m,其侧面与正面如图所示,则购买地毯至少需要多少元?
18.如图,在四边形ABCD中,AD∥BC,且AD(1)指出平移的方向和平移的距离;
(2)试说明AD+BC=BF.
真题练习
19.(2018?铜仁)如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC,△PB′C′的面积分别为S1,S2,则下列关系正确的是
A.S1>S2 B.S1参考答案
1.【答案】B
【解析】A.滑雪运动员在平坦的雪地上滑雪, 属于平移,故本选项错误;
B.彩票大转盘在旋转,不属于平移,故本选项正确;
C. 高楼的电梯在上上下下, 属于平移, 故本选项错误;
D. 火车在一段笔直的铁轨上行驶, 属于平移,故本选项错误.
故选:B.
4.【答案】A
【解析】根据网格结构,观察对应点A,D,点A向左平移5个单位,再向下平移2个单位即可到达点D的位置,所以平移步骤是:先把△ABC向左平移5个单位,再向下平移2个单位,故选A.
5.【答案】B
【解析】∵△ABE向右平移得到△DCF,∴AB∥CD,AE∥DF,∴∠DCF=∠B=45°,∴∠CDF=180°-
45°-60°=75°,∴∠AGC=∠DGE=180°-75°=105°,故选B.
6.【答案】C
【解析】已知,△ABE向右平移2 cm得到△DCF,根据平移的性质得到EF=AD=2 cm,AE=DF,又因△ABE的周长为16 cm,所以AB+BE+AE=16 cm,则四边形ABFD的周长=AB+BC+CF+DF+AD=16+2+
2=20(cm),故选C.
7.【答案】5
【解析】∵把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,∴三角板向右平移了5个单位,∴顶点C平移的距离CC′=5.故答案为:5.
8.【答案】45°
【解析】∵△ADE是由△DBF沿BD所在的直线平移得到的, ∴DE∥BC,∠BFD=∠AED, ∴∠AED=∠C ∴∠C=∠BFD=45°. 故答案是:45°.
9.【答案】30°,7
【解析】∵ 是ABC向右平移4 cm得到的,
∴BB′=CC′=4 cm,∠C′=∠ACB=30°,
∵B′C=3 cm,
∴B′C′=4+3=7 cm.
故答案为:30°,7.
12.【解析】如图:
13.【解析】由题意可知,长方形BEFC的面积为5×6=30cm2,
直角三角形ABC的面积为3×4÷2=6cm2,
30+6=36cm2.
∴三角形ABC所扫过的面积为36cm2.
14.【答案】C
【解析】如图,由题意和“两点之间线段最短”及“平行四边形的对边相等”可知,由A到B的最短距离的走法有下面三种:(1)由A→C→D→B;(2)由A→F→E→B;(3)由A→F→D→B,故选C.
17.【解析】利用平移线段,把楼梯的横竖向上向左平移,构成一个长方形,长、宽分别为5米,3米,∴地毯的长度为5+3=8(米),
∴地毯的面积为8×2=16(平方米),
∴买地毯至少需要16×32=512(元).
18.【解析】(1)平移的方向是点A到点D的方向,平移的距离是线段AD的长度; (2)∵ABC平移到DEF的位置, ∴CF=AD, ∵CF+BC=BF, ∴AD+BC=BF.
19.【答案】C
【解析】∵△ABC沿着BC方向平移得到△A′B′C′,∴AA′∥BC′,∵点P是直线AA′上任意一点,∴△ABC,△PB′C′的高相等,∴S1=S2,故选C.
5.4 平移
知识
1.平移的定义
(1)定义:把一个图形整体沿某一直线方向移动,会得到一个新的图形,图形的这种移动,叫做________.
(2)要素:一是平移的_________,二是平移的距离.
2.平移的性质
性质:平移后的新图形与原图形的形状和大小完全__________,即平移前后的两个图形的对应边__________(或在同一条直线上)且相等,对应角相等;连接各组对应点的线段平行(或在同一条直线上)且相等.
【注意】(1)连接对应点的线段的长度就是平移的距离.
(2)从原图形上一点到其对应点的方向即为平移的方向.
知识参考答案:
1.(1)平移(2)方向 2.相同,平行
重点
重点
平移的概念及其性质;利用平移作图
难点
探索平移的性质
易错
把握不准平移的方向和距离出错
一、平移的定义
把一个图形整体沿着某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
【例1】下列现象中,不属于平移的是
A.滑雪运动员在的平坦雪地上滑行 B.大楼上上下下地迎送来客的电梯
C.钟摆的摆动 D.火车在笔直的铁轨上飞驰而过
【答案】C
【解析】A.滑雪运动员在平坦的雪地上滑行,符合平移的定义,故不符合题意;
B.大楼电梯上上下下地迎送来客,是平移,故不符合题意;
C.钟摆的摆动不是平移,故符合题意;
D.火车在笔直的铁轨上飞驰而过,是平移,故不符合题意;
故答案为C.
【例2】观察下列图案,能通过如图的图形平移得到的是
A. B.
C. D.
【答案】D
【解析】通过图案平移得到必须与题中已知图案完全相同,角度也必须相同,
观察图形可知C可以通过题中已知图案平移得到.
故选D.
二、平移的性质
1.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行且相等.
2.平移的特征:(1)平移不改变图形的形状和大小;(2)连接各组对应点的线段平行且相等.
【例3】如图,在△ABC中,BC=5,∠A=70°,∠B=75°,把△ABC沿直线BC的方向平移到△DEF的位置,若CF=3,则下列结论中错误的是
A.BE=3 B.∠F=35° C.DF=5 D.AB∥DE
【答案】C
【解析】∵∠A=70°,∠B=75°,∴∠ACB=35°,∵△DEF由△ABC平移得到,∴BC=EF=5,∠F=∠ACB=
35°,AB∥DE,∴B、D选项正确;∵CF=3,∴EC=2,∴BE=3,故A选项正确;C选项DF的长度不能求出,故C选项错误,故选C.
【例4】下列图案只用其中一部分平移就可得到的是
A. B.
C. D.
【答案】B
【解析】A、通过平移得不到,故错误;
B、图形的形状和大小不变,符合平移性质,故正确;
C、通过平移得不到,故错误;
D、最后一个形状不同,故错误.
故选B.
三、平移的应用
在解决面积问题时,如果图形是不规则图形或者是由几个图形组成的,可设法将图形转化为规则的图形求面积,平移可作为其中的一种手段.
【例5】若在运动会颁奖台上面及两侧铺上地毯(如图阴影部分),长为m,宽为n,高为h,(单位为:cm).
(1)用m,n,h表示需要地毯的面积;
(2)若m=160,n=60,h=80,求地毯的面积.
【答案】(1)mn+2nh;(2)19200 cm2
【解析】(1)地毯的面积为:(m+2h)n=mn+2nh.
(2)地毯总长:80×2+160=320(cm),
320×60=19200(cm2),
答:地毯的面积为19200 cm2.
【例6】如图,在一块长为a m,宽为b m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1 m就是它的右边线,则这块草地的绿地面积为
A.(a-1)b B.a(b-1)
C.ab-1 D.(a-1)(b-1)
【答案】A
【解析】小路的左边线向右平移1 m就是它的右边线,路的宽度是1 m,绿地的长是(a?1)m,绿地的面积是(a?1)b,故选A.
基础训练
1.下列现象中不属于平移的是
A.滑雪运动员在平坦的雪地上滑雪 B.彩票大转盘在旋转
C.高楼的电梯在上上下下 D.火车在一段笔直的铁轨上行驶
2.如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有
A.0条 B.1条
C.2条 D.3条
3.如图,△FDE经过怎样的平移可得到△ABC
A.沿射线EC的方向移动DB长 B.沿射线CE的方向移动DB长
C.沿射线EC的方向移动CD长 D.沿射线BD的方向移动BD长
4.如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是
A.先向左平移5个单位,再向下平移2个单位
B.先向右平移5个单位,再向下平移2个单位
C.先向左平移5个单位,再向上平移2个单位
D.先向右平移5个单位,再向下平移2个单位
5.如图,将△ABE向右平移得到△DCF,与交于点,其中,,则
A. B. C. D.
6.如图,将△ABE向右平移2 cm得到△DCF,如果△ABE的周长是16 cm,那么四边形ABFD的周长是
A.16 cm B.18 cm C.20 cm D.21 cm
7.如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC'=____.
8.如图,三角形ADE是由三角形DBF沿BD所在的直线平移得到的,AE,BF的延长线交于点C.若∠BFD=45°,则∠C的度数是 ________
9.如图, 是ABC向右平移4 cm得到的,已知∠ACB=30°,B′C=3 cm,则∠C′=_________,B′C′=________cm.
10.要在台阶上铺设某种红地毯,已知这种红地毯每平方米的售价是40元,台阶宽为3米,侧面如图所示.购买这种红地毯至少需要__________元.
11.如图,△ABC沿直线BC向右移了3 cm,得△FDE,且BC=6 cm,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
12.如图,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F的位置,并作出△DEF.
13.如图,在三角形ABC中,已知AB=3cm,AC=4cm,BC=5cm.现将三角形ABC沿着垂直于BC的方向平移6cm,到三角形DEF的位置,求三角形ABC所扫过的面积.
能力测试
14.如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中已有的线段走,那么从A点到B点的最短距离的走法共有
A.1种 B.2种
C.3种 D.4种
15.多边形的相邻两边互相垂直,则这个多边形的周长为
A.a+b B.2a+b
C.2a+2b D.2b+a
16.如图,平移ABC可得到DEF,如果∠C=60°,AE=7cm,AB=4cm,那么∠F= ______ 度,DB= ______ cm.
17.如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种红色地毯的售价为每平方米32元,主楼梯宽为2 m,其侧面与正面如图所示,则购买地毯至少需要多少元?
18.如图,在四边形ABCD中,AD∥BC,且AD
(2)试说明AD+BC=BF.
真题练习
19.(2018?铜仁)如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC,△PB′C′的面积分别为S1,S2,则下列关系正确的是
A.S1>S2 B.S1
1.【答案】B
【解析】A.滑雪运动员在平坦的雪地上滑雪, 属于平移,故本选项错误;
B.彩票大转盘在旋转,不属于平移,故本选项正确;
C. 高楼的电梯在上上下下, 属于平移, 故本选项错误;
D. 火车在一段笔直的铁轨上行驶, 属于平移,故本选项错误.
故选:B.
4.【答案】A
【解析】根据网格结构,观察对应点A,D,点A向左平移5个单位,再向下平移2个单位即可到达点D的位置,所以平移步骤是:先把△ABC向左平移5个单位,再向下平移2个单位,故选A.
5.【答案】B
【解析】∵△ABE向右平移得到△DCF,∴AB∥CD,AE∥DF,∴∠DCF=∠B=45°,∴∠CDF=180°-
45°-60°=75°,∴∠AGC=∠DGE=180°-75°=105°,故选B.
6.【答案】C
【解析】已知,△ABE向右平移2 cm得到△DCF,根据平移的性质得到EF=AD=2 cm,AE=DF,又因△ABE的周长为16 cm,所以AB+BE+AE=16 cm,则四边形ABFD的周长=AB+BC+CF+DF+AD=16+2+
2=20(cm),故选C.
7.【答案】5
【解析】∵把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,∴三角板向右平移了5个单位,∴顶点C平移的距离CC′=5.故答案为:5.
8.【答案】45°
【解析】∵△ADE是由△DBF沿BD所在的直线平移得到的, ∴DE∥BC,∠BFD=∠AED, ∴∠AED=∠C ∴∠C=∠BFD=45°. 故答案是:45°.
9.【答案】30°,7
【解析】∵ 是ABC向右平移4 cm得到的,
∴BB′=CC′=4 cm,∠C′=∠ACB=30°,
∵B′C=3 cm,
∴B′C′=4+3=7 cm.
故答案为:30°,7.
12.【解析】如图:
13.【解析】由题意可知,长方形BEFC的面积为5×6=30cm2,
直角三角形ABC的面积为3×4÷2=6cm2,
30+6=36cm2.
∴三角形ABC所扫过的面积为36cm2.
14.【答案】C
【解析】如图,由题意和“两点之间线段最短”及“平行四边形的对边相等”可知,由A到B的最短距离的走法有下面三种:(1)由A→C→D→B;(2)由A→F→E→B;(3)由A→F→D→B,故选C.
17.【解析】利用平移线段,把楼梯的横竖向上向左平移,构成一个长方形,长、宽分别为5米,3米,∴地毯的长度为5+3=8(米),
∴地毯的面积为8×2=16(平方米),
∴买地毯至少需要16×32=512(元).
18.【解析】(1)平移的方向是点A到点D的方向,平移的距离是线段AD的长度; (2)∵ABC平移到DEF的位置, ∴CF=AD, ∵CF+BC=BF, ∴AD+BC=BF.
19.【答案】C
【解析】∵△ABC沿着BC方向平移得到△A′B′C′,∴AA′∥BC′,∵点P是直线AA′上任意一点,∴△ABC,△PB′C′的高相等,∴S1=S2,故选C.
