人教版七年级数学下册7.1 平面直角坐标系教案(知识讲解+巩固练习)
文档属性
| 名称 | 人教版七年级数学下册7.1 平面直角坐标系教案(知识讲解+巩固练习) |

|
|
| 格式 | zip | ||
| 文件大小 | 447.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-26 22:56:44 | ||
图片预览




文档简介
第七章 平面直角坐标系
7.1 平面直角坐标系
知识
1.有序数对
(1)定义:有顺序的两个数a与b组成的数对叫做__________.记作:(a,b).
注意:(1)两数中间有“,”两边有括号;(2)数对(a,b)与(b,a)不同.
(2)有序数对的作用:利用有序数对可以在平面内准确表示一个位置.
2.平面直角坐标系
(1)定义:满足一下条件的两条数轴叫做平面直角坐标系:①原点重合;②互相垂直;③习惯上取向__________、向__________为正方向,单位长度一般取相同.
(2)由点找坐标的方法
过点作x轴的垂线,垂足在x轴上对应的数a就是点的横坐标;
过点作y轴的垂线,垂足在y轴上对应的数b就是点的纵坐标.
有序数对(a,b)就是点的坐标.
(3)由坐标找点的方法
先找到表示横坐标与纵坐标的点,然后过这两点分别作x轴与y轴的垂线,垂线的交点就是该坐标对应的点.
3.点的坐标特征
4.特殊位置点的坐标
(1)平行于坐标轴的点的坐标
平行于横轴的直线上的点的纵坐标相同;平行于纵轴的直线上的点的横坐标相同.
(2)象限角平分线上的点的坐标
知识参考答案:
1.(1)有序数对(2)右,上
重点
重点
理解有序数对的意义和作用,平面直角坐标系和点的坐标
难点
用有序数对表示点的位置,根据点的位置写出点的坐标,根据点的坐标描出点的位置
易错
确定点的坐标时误判横、纵坐标,确定所在象限时漏解
一、有序数对
1.理解有序数对的概念有两个要点:一是“有序”,二是“数对”,“数对”是指有两个数.
2.有序数对一般用来表示位置,如用“排”“列”表示教师内座位的位置,用经纬度表示地球上的地点等.
【例1】王东坐在教室的第3列第2行,用(3,2)表示,李军坐在王东正后方的第一个位置上,李军的位置是
A.(4,3) B.(3,4) C.(1,3) D.(3,3)
【答案】D
【解析】王东坐在教室的第3列第2行,用(3,2)表示,王军坐在王东正后方的第一个位置上,则说明王军与王东在同一列,王军是在第2+1=3(行),所以王军的位置是(3,3),故选D.
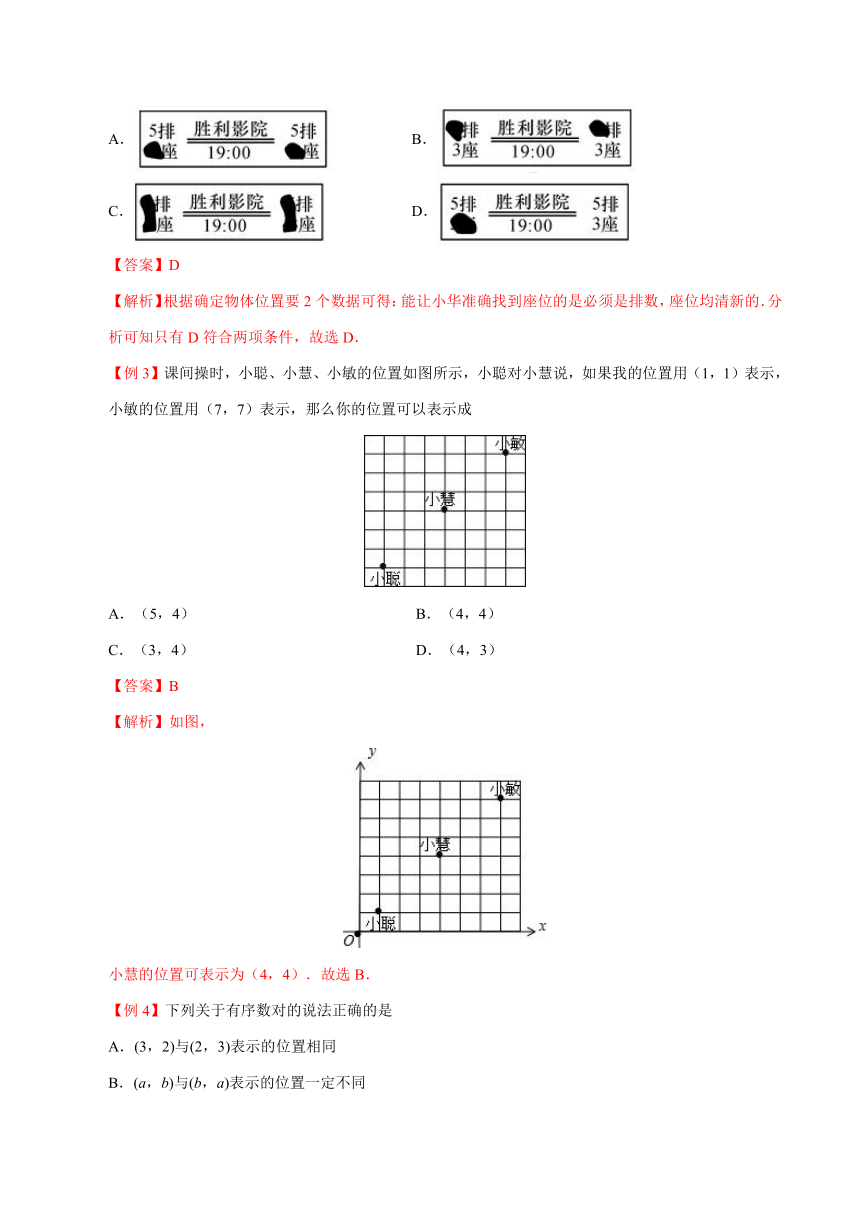
【例2】下列有污迹的电影票中能让小华准确找到座位的是
A. B.
C. D.
【答案】D
【解析】根据确定物体位置要2个数据可得:能让小华准确找到座位的是必须是排数,座位均清新的.分析可知只有D符合两项条件,故选D.
【例3】课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成
A.(5,4) B.(4,4)
C.(3,4) D.(4,3)
【答案】B
【解析】如图,
小慧的位置可表示为(4,4).故选B.
【例4】下列关于有序数对的说法正确的是
A.(3,2)与(2,3)表示的位置相同
B.(a,b)与(b,a)表示的位置一定不同
C.(3,–2)与(–2,3)是表示不同位置的两个有序数对
D.(4,4)与(4,4)表示两个不同的位置
【答案】C
【解析】(3,2)与(2,3)表示的位置不相同,A选项错误;
当a=b时,(a,b)与(b,a)表示的位置相同,B选项错误;
(3,–2)与(–2,3)是表示不同位置的两个有序数对,C选项正确;
(4,4)与(4,4)表示两个相同的位置,D选项错误.
故选C.
【例5】下列关于有序数对的说法正确的是
A.(3,2)与(2,3)表示的位置相同
B.(a,b)与(b,a)表示的位置一定不同
C.(3,-2)与(-2,3)是表示不同位置的两个有序数对
D.(4,4)与(4,4)表示两个不同的位置
【例6】如果将一张“13排10号”的电影票记为(13,10),那么“3排8号”的电影票应记为__________,(10,13)表示的电影票是__________.
【答案】(3,8);10排13号
【解析】∵“13排10号”的电影票记为(13,10),∴“3排8号”的电影票应记为(3,8),(10,13)的电影票表示为10排13号,故答案为:(3,8);10排13号.
二、平面直角坐标系
1.在建立平面直角坐标系时要适当,一般建立时能使表示的点的坐标越简单、越容易表示就越适当.
2.在建立平面直角坐标系时要首先规定谁是x轴、谁是y轴,谁是原点、正方向,并规定了适当的单位长度,然后再用坐标确定点的位置.
3.在写点的坐标时,必须先写横坐标,再写纵坐标,中间用逗号隔开.平面上的任意一点都有唯一的一对有序数对(即这个点的坐标)与之对应,反过来,对于任意一对有序数对,平面上都有唯一的一个点与之对应.
【例7】在平面直角坐标系中,点A(2,-3)在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【解析】因为点A(2,-3)的横坐标是正数,纵坐标是负数,所以点A在平面直角坐标系的第四象限
故选D.
【例8】在平面直角坐标系中,点P在x轴的下方,y轴右侧,且到x轴的距离为5,到y轴距离为1,则点P的坐标为
A.(1,–5) B.(5,1)
C.(–1,5) D.(5,–1)
【答案】A
【解析】∵点P在x轴下方,y轴的右侧,∴点P在第四象限.
∵点P到x轴的距离为5,到y轴的距离为1,∴点P的横坐标为1,纵坐标为–5,
∴点P的坐标为(1,–5).故选A.
【例9】如图,小手盖住的点的坐标可能为
A.(5,2) B.(–6,3)
C.(–4,–6) D.(3,–4)
【答案】C
【解析】根据图示,小手盖住的点在第三象限,第三象限的点坐标特点是:横负纵负;
分析选项可得只有C符合.故选C.
【例10】已知点P(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是
A.(3,3) B.(6,-6)
C.(3,-3) D.(3,3)或(6,-6)
【答案】D
【解析】因为点P(2-a,3a+6)到两坐标轴的距离相等,所以|2-a|=|3a+6|,所以2-a=3a+6或2-a=
-(3a+6),解得a=-1或a=-4.当a=-1时,2-a=2-(-1)=2+1=3;当a=-4时,2-a=2-(-4)=2+4=6,所以点P的坐标为(3,3)或(6,-6),故选D.
【例11】象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“马”和“车”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为
A.(3,2) B.(1,3)
C.(0,3) D.(-3,3)
【答案】B
【解析】表示棋子“马”的点的坐标分别为(4,3),向左平移3个单位长度,得表示棋子“炮”的点的坐标为(1,3),故选B.
【例12】在如图所示的直角坐标系中描出下列各点:A(-2,0),B(2,5),C(-,-3).
【解析】如图所示:
【名师点睛】本题考查了点的坐标,熟练掌握平面直角坐标系中点的表示方法是解题的关键.
【例13】如图,建立适当的直角坐标系,并写出这个四角星的八个顶点的坐标.
【解析】建立如图所示的平面直角坐标系:
八个顶点的坐标分别是:(6,0),(2,2),(0,6),(-2,2),(-6,0)(-2,-2),(0,-6),(2,-2).
基础训练
1.确定平面直角坐标系内点的位置是
A.一个实数 B.一个整数
C.一对实数 D.有序实数对
2.下列描述,能够确定一个点的位置的是
A.国家大剧院第三排 B.北偏东
C.东经,北纬 D.北京市西南
3.在坐标平面内,下列各点中到x轴的距离最近的点是
A.(2,5) B.(–4,1)
C.(3,–4) D.(6,2)
4.下列有污迹的电影票中能让小华准确找到座位的是
A. B.
C. D.
5.若点P(m,1–2m)的横坐标与纵坐标互为相反数,则点P一定在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
6.若点A(–2,n)在x轴上,则点B(n–2,n+1)在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.已知M(1,–2),N(–3,–2),则直线MN与x轴,y轴的位置关系分别为
A.相交,相交 B.平行,平行
C.垂直,平行 D.平行,垂直
8.电影院里的座位按“×排×号”编排,小明的座位简记为(12,6),小菲的位置简记为(12,12),则小明与小菲坐的位置为
A.同一排 B.前后同一条直线上
C.中间隔六个人 D.前后隔六排
9.在平面直角坐标系xOy中,若A点坐标为(–3,3),B点坐标为(2,0),则三角形ABO的面积为
A.15 B.7.5
C.6 D.3
10.在平面直角坐标系中,点(-4,4)在第__________象限.
11.若点A的坐标是(-3,5),则它到x轴的距离是__________,到y轴的距离是__________.
12.已知点A(-3,2),点B(1,4).
(1)若CA平行于x轴,BC平行于y轴,则点C的坐标是__________;
(2)若CA平行于y轴,BC平行于x轴,则点C的坐标是__________.
13.如下图所示,A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格?
14.如图中标明了小英家附近的一些地方,以小英家为坐标原点建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2)→(3,-1)→(0,-1)→(-1,-2)→(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
能力测试
15.如图,正方形ABCD的点A和点C的坐标分别为(-2,3)和(3,-2),则点B和点D的坐标分别为
A.(2,2)和(3,3) B.(-2,-2)和(3,3)
C.(-2,-2)和(-3,-3) D.(2,2)和(-3,-3)
16.若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在象限是
A.第一象限或第三象限 B.第二象限或第四象限
C.第一象限或第二象限 D.不能确定
17.已知点A(2a-6,-4)在二、四象限的角平分线上,则a=__________.
真题练习
18.(2018?大连)在平面直角坐标系中,点(–3,2)所在的象限是
A.第一象限 B.第二象限
C.第三象限 D.第四象限
19.(2018?扬州)在平面直角坐标系的第二象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是
A.(3,–4) B.(4,–3)
C.(–4,3) D.(–3,4)
20.(2018?临安区)P(3,–4)到x轴的距离是__________.
21.(2018?柳州)如图,在平面直角坐标系中,点A的坐标是__________.
22.(2018?鄂尔多斯)在平面直角坐标系中,对于点P(a,b),我们把Q(–b+1,a+1)叫做点P的伴随点,已知A1的伴随点为A2,A2的伴随点为A3,…,这样依次下去得到A1,A2,A3,…,An,若A1的坐标为(3,1),则A2018的坐标为__________.
参考答案
1.【答案】D
【解析】两个实数组成的有序数对,故选D.
2.【答案】C
【解析】A、国家大剧院第三排,不能够确定一个点的位置,故本选项错误; B、北偏东,不能够确定一个点的位置,故本选项错误; C、东经,北纬能够确定一个点的位置,故本选项正确; D、北京市西南,不能够确定一个点的位置,故本选项错误. 故选C.
3.【答案】B
【解析】A选项中的点到x轴的距离是|5|=5,B选项中的点到x轴的距离是|1|=1,C选项中的点到x轴的距离为|–4|=4,D选项中的点到x轴的距离是|2|=2.故选B.
4.【答案】D
【解析】根据确定物体位置要2个数据可得:能让小华准确找到座位的必须是排数,座位均清晰的.分析可知只有D符合两项条件,故选D.
8.【答案】A
【解析】∵(12,6)表示12排6号,(12,12)表示12排12号,∴小明(12,6)与小菲(12,12)应坐的位置在同一排,中间隔5人.故选A.
9.【答案】D
【解析】易知点A到x轴的距离为3,OB=2,∴,故选D.
10.【答案】二
【解析】在平面直角坐标系中,点(-4,4)在第二象限,故答案为:二.
11.【答案】5;3
【解析】根据平面直角坐标系的特点,点到x轴的距离是|y|=5,点到y轴的距离为|x|=3,
故答案为:5;3.
12.【答案】(1,2);(-3,4)
【解析】(1)若平行于轴,平行于轴,则点的横坐标等于点的横坐标,点的纵坐标等于点的纵坐标,点的坐标为:(1,2);(2)若平行于轴,平行于轴,则点的横坐标等于点的横坐标,点的纵坐标等于点的纵坐标,点的坐标为:(-3,4),故答案为:(1,2); (-3,4).
13.【解析】如下图所示,可知小明与小刚相距3个格.
14.【解析】(1)汽车站(1,1),消防站(2,-2).
(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
17.【答案】5
【解析】由题意得2a-6=4,解得a=5,故答案为:5.
18.【答案】B
【解析】点(–3,2)所在的象限在第二象限.故选B.
19.【答案】C
【解析】由题意,得x=–4,y=3,即M点的坐标是(–4,3),故选C.
20.【答案】4
【解析】根据点在坐标系中坐标的几何意义可知,P(3,–4)到x轴的距离是|–4|=4.故答案为:4.
21.【答案】(–2,3)
【解析】由坐标系可得:点A的坐标是(–2,3).故答案为:(–2,3).
7.1 平面直角坐标系
知识
1.有序数对
(1)定义:有顺序的两个数a与b组成的数对叫做__________.记作:(a,b).
注意:(1)两数中间有“,”两边有括号;(2)数对(a,b)与(b,a)不同.
(2)有序数对的作用:利用有序数对可以在平面内准确表示一个位置.
2.平面直角坐标系
(1)定义:满足一下条件的两条数轴叫做平面直角坐标系:①原点重合;②互相垂直;③习惯上取向__________、向__________为正方向,单位长度一般取相同.
(2)由点找坐标的方法
过点作x轴的垂线,垂足在x轴上对应的数a就是点的横坐标;
过点作y轴的垂线,垂足在y轴上对应的数b就是点的纵坐标.
有序数对(a,b)就是点的坐标.
(3)由坐标找点的方法
先找到表示横坐标与纵坐标的点,然后过这两点分别作x轴与y轴的垂线,垂线的交点就是该坐标对应的点.
3.点的坐标特征
4.特殊位置点的坐标
(1)平行于坐标轴的点的坐标
平行于横轴的直线上的点的纵坐标相同;平行于纵轴的直线上的点的横坐标相同.
(2)象限角平分线上的点的坐标
知识参考答案:
1.(1)有序数对(2)右,上
重点
重点
理解有序数对的意义和作用,平面直角坐标系和点的坐标
难点
用有序数对表示点的位置,根据点的位置写出点的坐标,根据点的坐标描出点的位置
易错
确定点的坐标时误判横、纵坐标,确定所在象限时漏解
一、有序数对
1.理解有序数对的概念有两个要点:一是“有序”,二是“数对”,“数对”是指有两个数.
2.有序数对一般用来表示位置,如用“排”“列”表示教师内座位的位置,用经纬度表示地球上的地点等.
【例1】王东坐在教室的第3列第2行,用(3,2)表示,李军坐在王东正后方的第一个位置上,李军的位置是
A.(4,3) B.(3,4) C.(1,3) D.(3,3)
【答案】D
【解析】王东坐在教室的第3列第2行,用(3,2)表示,王军坐在王东正后方的第一个位置上,则说明王军与王东在同一列,王军是在第2+1=3(行),所以王军的位置是(3,3),故选D.
【例2】下列有污迹的电影票中能让小华准确找到座位的是
A. B.
C. D.
【答案】D
【解析】根据确定物体位置要2个数据可得:能让小华准确找到座位的是必须是排数,座位均清新的.分析可知只有D符合两项条件,故选D.
【例3】课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成
A.(5,4) B.(4,4)
C.(3,4) D.(4,3)
【答案】B
【解析】如图,
小慧的位置可表示为(4,4).故选B.
【例4】下列关于有序数对的说法正确的是
A.(3,2)与(2,3)表示的位置相同
B.(a,b)与(b,a)表示的位置一定不同
C.(3,–2)与(–2,3)是表示不同位置的两个有序数对
D.(4,4)与(4,4)表示两个不同的位置
【答案】C
【解析】(3,2)与(2,3)表示的位置不相同,A选项错误;
当a=b时,(a,b)与(b,a)表示的位置相同,B选项错误;
(3,–2)与(–2,3)是表示不同位置的两个有序数对,C选项正确;
(4,4)与(4,4)表示两个相同的位置,D选项错误.
故选C.
【例5】下列关于有序数对的说法正确的是
A.(3,2)与(2,3)表示的位置相同
B.(a,b)与(b,a)表示的位置一定不同
C.(3,-2)与(-2,3)是表示不同位置的两个有序数对
D.(4,4)与(4,4)表示两个不同的位置
【例6】如果将一张“13排10号”的电影票记为(13,10),那么“3排8号”的电影票应记为__________,(10,13)表示的电影票是__________.
【答案】(3,8);10排13号
【解析】∵“13排10号”的电影票记为(13,10),∴“3排8号”的电影票应记为(3,8),(10,13)的电影票表示为10排13号,故答案为:(3,8);10排13号.
二、平面直角坐标系
1.在建立平面直角坐标系时要适当,一般建立时能使表示的点的坐标越简单、越容易表示就越适当.
2.在建立平面直角坐标系时要首先规定谁是x轴、谁是y轴,谁是原点、正方向,并规定了适当的单位长度,然后再用坐标确定点的位置.
3.在写点的坐标时,必须先写横坐标,再写纵坐标,中间用逗号隔开.平面上的任意一点都有唯一的一对有序数对(即这个点的坐标)与之对应,反过来,对于任意一对有序数对,平面上都有唯一的一个点与之对应.
【例7】在平面直角坐标系中,点A(2,-3)在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【解析】因为点A(2,-3)的横坐标是正数,纵坐标是负数,所以点A在平面直角坐标系的第四象限
故选D.
【例8】在平面直角坐标系中,点P在x轴的下方,y轴右侧,且到x轴的距离为5,到y轴距离为1,则点P的坐标为
A.(1,–5) B.(5,1)
C.(–1,5) D.(5,–1)
【答案】A
【解析】∵点P在x轴下方,y轴的右侧,∴点P在第四象限.
∵点P到x轴的距离为5,到y轴的距离为1,∴点P的横坐标为1,纵坐标为–5,
∴点P的坐标为(1,–5).故选A.
【例9】如图,小手盖住的点的坐标可能为
A.(5,2) B.(–6,3)
C.(–4,–6) D.(3,–4)
【答案】C
【解析】根据图示,小手盖住的点在第三象限,第三象限的点坐标特点是:横负纵负;
分析选项可得只有C符合.故选C.
【例10】已知点P(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是
A.(3,3) B.(6,-6)
C.(3,-3) D.(3,3)或(6,-6)
【答案】D
【解析】因为点P(2-a,3a+6)到两坐标轴的距离相等,所以|2-a|=|3a+6|,所以2-a=3a+6或2-a=
-(3a+6),解得a=-1或a=-4.当a=-1时,2-a=2-(-1)=2+1=3;当a=-4时,2-a=2-(-4)=2+4=6,所以点P的坐标为(3,3)或(6,-6),故选D.
【例11】象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“马”和“车”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为
A.(3,2) B.(1,3)
C.(0,3) D.(-3,3)
【答案】B
【解析】表示棋子“马”的点的坐标分别为(4,3),向左平移3个单位长度,得表示棋子“炮”的点的坐标为(1,3),故选B.
【例12】在如图所示的直角坐标系中描出下列各点:A(-2,0),B(2,5),C(-,-3).
【解析】如图所示:
【名师点睛】本题考查了点的坐标,熟练掌握平面直角坐标系中点的表示方法是解题的关键.
【例13】如图,建立适当的直角坐标系,并写出这个四角星的八个顶点的坐标.
【解析】建立如图所示的平面直角坐标系:
八个顶点的坐标分别是:(6,0),(2,2),(0,6),(-2,2),(-6,0)(-2,-2),(0,-6),(2,-2).
基础训练
1.确定平面直角坐标系内点的位置是
A.一个实数 B.一个整数
C.一对实数 D.有序实数对
2.下列描述,能够确定一个点的位置的是
A.国家大剧院第三排 B.北偏东
C.东经,北纬 D.北京市西南
3.在坐标平面内,下列各点中到x轴的距离最近的点是
A.(2,5) B.(–4,1)
C.(3,–4) D.(6,2)
4.下列有污迹的电影票中能让小华准确找到座位的是
A. B.
C. D.
5.若点P(m,1–2m)的横坐标与纵坐标互为相反数,则点P一定在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
6.若点A(–2,n)在x轴上,则点B(n–2,n+1)在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.已知M(1,–2),N(–3,–2),则直线MN与x轴,y轴的位置关系分别为
A.相交,相交 B.平行,平行
C.垂直,平行 D.平行,垂直
8.电影院里的座位按“×排×号”编排,小明的座位简记为(12,6),小菲的位置简记为(12,12),则小明与小菲坐的位置为
A.同一排 B.前后同一条直线上
C.中间隔六个人 D.前后隔六排
9.在平面直角坐标系xOy中,若A点坐标为(–3,3),B点坐标为(2,0),则三角形ABO的面积为
A.15 B.7.5
C.6 D.3
10.在平面直角坐标系中,点(-4,4)在第__________象限.
11.若点A的坐标是(-3,5),则它到x轴的距离是__________,到y轴的距离是__________.
12.已知点A(-3,2),点B(1,4).
(1)若CA平行于x轴,BC平行于y轴,则点C的坐标是__________;
(2)若CA平行于y轴,BC平行于x轴,则点C的坐标是__________.
13.如下图所示,A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格?
14.如图中标明了小英家附近的一些地方,以小英家为坐标原点建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2)→(3,-1)→(0,-1)→(-1,-2)→(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
能力测试
15.如图,正方形ABCD的点A和点C的坐标分别为(-2,3)和(3,-2),则点B和点D的坐标分别为
A.(2,2)和(3,3) B.(-2,-2)和(3,3)
C.(-2,-2)和(-3,-3) D.(2,2)和(-3,-3)
16.若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在象限是
A.第一象限或第三象限 B.第二象限或第四象限
C.第一象限或第二象限 D.不能确定
17.已知点A(2a-6,-4)在二、四象限的角平分线上,则a=__________.
真题练习
18.(2018?大连)在平面直角坐标系中,点(–3,2)所在的象限是
A.第一象限 B.第二象限
C.第三象限 D.第四象限
19.(2018?扬州)在平面直角坐标系的第二象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是
A.(3,–4) B.(4,–3)
C.(–4,3) D.(–3,4)
20.(2018?临安区)P(3,–4)到x轴的距离是__________.
21.(2018?柳州)如图,在平面直角坐标系中,点A的坐标是__________.
22.(2018?鄂尔多斯)在平面直角坐标系中,对于点P(a,b),我们把Q(–b+1,a+1)叫做点P的伴随点,已知A1的伴随点为A2,A2的伴随点为A3,…,这样依次下去得到A1,A2,A3,…,An,若A1的坐标为(3,1),则A2018的坐标为__________.
参考答案
1.【答案】D
【解析】两个实数组成的有序数对,故选D.
2.【答案】C
【解析】A、国家大剧院第三排,不能够确定一个点的位置,故本选项错误; B、北偏东,不能够确定一个点的位置,故本选项错误; C、东经,北纬能够确定一个点的位置,故本选项正确; D、北京市西南,不能够确定一个点的位置,故本选项错误. 故选C.
3.【答案】B
【解析】A选项中的点到x轴的距离是|5|=5,B选项中的点到x轴的距离是|1|=1,C选项中的点到x轴的距离为|–4|=4,D选项中的点到x轴的距离是|2|=2.故选B.
4.【答案】D
【解析】根据确定物体位置要2个数据可得:能让小华准确找到座位的必须是排数,座位均清晰的.分析可知只有D符合两项条件,故选D.
8.【答案】A
【解析】∵(12,6)表示12排6号,(12,12)表示12排12号,∴小明(12,6)与小菲(12,12)应坐的位置在同一排,中间隔5人.故选A.
9.【答案】D
【解析】易知点A到x轴的距离为3,OB=2,∴,故选D.
10.【答案】二
【解析】在平面直角坐标系中,点(-4,4)在第二象限,故答案为:二.
11.【答案】5;3
【解析】根据平面直角坐标系的特点,点到x轴的距离是|y|=5,点到y轴的距离为|x|=3,
故答案为:5;3.
12.【答案】(1,2);(-3,4)
【解析】(1)若平行于轴,平行于轴,则点的横坐标等于点的横坐标,点的纵坐标等于点的纵坐标,点的坐标为:(1,2);(2)若平行于轴,平行于轴,则点的横坐标等于点的横坐标,点的纵坐标等于点的纵坐标,点的坐标为:(-3,4),故答案为:(1,2); (-3,4).
13.【解析】如下图所示,可知小明与小刚相距3个格.
14.【解析】(1)汽车站(1,1),消防站(2,-2).
(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
17.【答案】5
【解析】由题意得2a-6=4,解得a=5,故答案为:5.
18.【答案】B
【解析】点(–3,2)所在的象限在第二象限.故选B.
19.【答案】C
【解析】由题意,得x=–4,y=3,即M点的坐标是(–4,3),故选C.
20.【答案】4
【解析】根据点在坐标系中坐标的几何意义可知,P(3,–4)到x轴的距离是|–4|=4.故答案为:4.
21.【答案】(–2,3)
【解析】由坐标系可得:点A的坐标是(–2,3).故答案为:(–2,3).
