人教版七年级数学下册7.2 坐标方法的简单应用教案(知识讲解+巩固练习)
文档属性
| 名称 | 人教版七年级数学下册7.2 坐标方法的简单应用教案(知识讲解+巩固练习) |

|
|
| 格式 | zip | ||
| 文件大小 | 678.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-26 00:00:00 | ||
图片预览



文档简介
第七章 平面直角坐标系
7.2 坐标方法的简单应用
知识
1.用坐标表示地理位置
用坐标表示地理位置的过程和方法
(1)建立坐标系,选择一个__________参照点为原点,确定__________的__________.参照点不同,地理位置的坐标也不同.
(2)根据具体问题确定__________.
(3)在坐标平面内画出这些点,并写出各点的__________和各个地点的__________.
2.用坐标表示平移
在平面直角坐标系中,
(1)将点(x,y)向右平移a个单位长度,对应点的横坐标__________a,而纵坐标不变,即坐标变为__________.
(2)将点(x,y)向左平移a个单位长度,对应点的横坐标__________a,而纵坐标不变,即坐标变为__________.
(3)将点(x,y)向下平移a个单位长度,对应点的纵坐标__________a,而横坐标不变,即坐标变为__________.
(4)将点(x,y)向上平移a个单位长度,对应点的纵坐标__________a,而横坐标不变,即坐标变为__________.
3.图形上点的坐标变化与图形平移间的关系
(1)横坐标变化,纵坐标不变:
原图形上的点(x,y)向右平移a个单位
原图形上的点(x,y)向左平移a个单位
(2)横坐标不变,纵坐标变化:
原图形上的点(x,y)向上平移b个单位
原图形上的点(x,y)向下平移b个单位
(3)横坐标、纵坐标都变化:
原图形上的点(x,y)向右平移a个单位,向上平移b个单位
原图形上的点(x,y)向右平移a个单位,向下平移b个单位
原图形上的点(x,y)向左平移a个单位,向上平移b个单位
原图形上的点(x,y)向左平移a个单位,向下平移b个单位
知识参考答案:
1.(1)适当的,x轴和y轴,正方向(2)单位长度(3)坐标,名称2.(1)加上,(x+a,y)(2)减去,(x-a,y)(3)减去,(x,y-a)(4)加上,(x,y+a)
重点
重点
建立适当的平面直角坐标系表示地理位置,掌握坐标变化与图形平移的关系,利用坐标变化与图形平移的关系解决实际问题
难点
建立适当的平面直角坐标系,平面直角坐标系中,点的平移与图形的平移的关系
易错
混淆点的坐标的平移规律
一、用坐标表示地理位置
1.确定坐标原点
用坐标表示地理位置时,要注意选择适当的位置为坐标原点,这里所说的适当,通常要么是比较有名的地点,要么是所要绘制的区域内较居中的位置.不同的原点产生的地理位置的坐标也不同.原点不同,地理位置的坐标也不同.用适当的位置表示原点,可以降低计算的难度.
2.如何确定x轴与y轴的方向
坐标轴的方向通常是选择以水平线为x轴,以向右为正方向(正东),以竖直线为y轴,以向上为正方向(正北),这样可以使东西南北的方向与地理位置的方向保持一致.
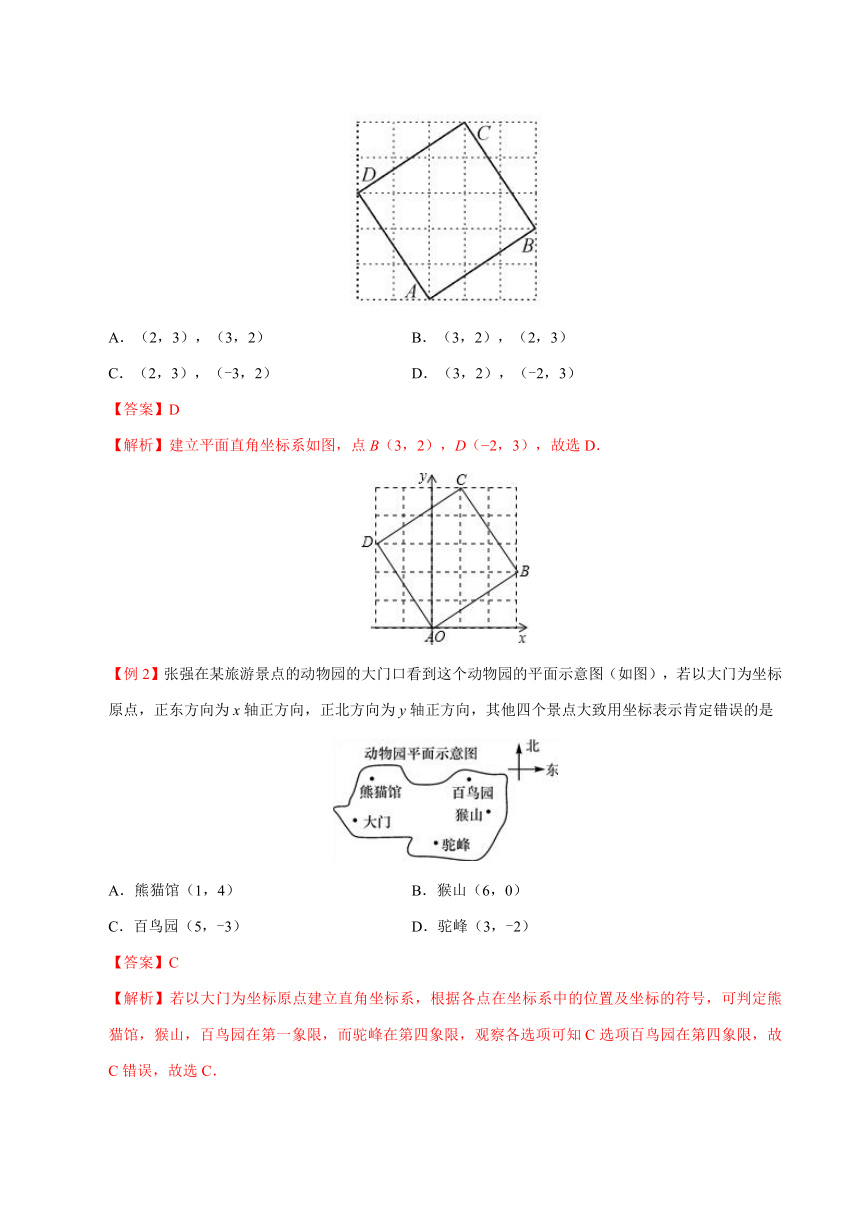
【例1】如图,是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为
A.(2,3),(3,2) B.(3,2),(2,3)
C.(2,3),(-3,2) D.(3,2),(-2,3)
【答案】D
【解析】建立平面直角坐标系如图,点B(3,2),D(?2,3),故选D.
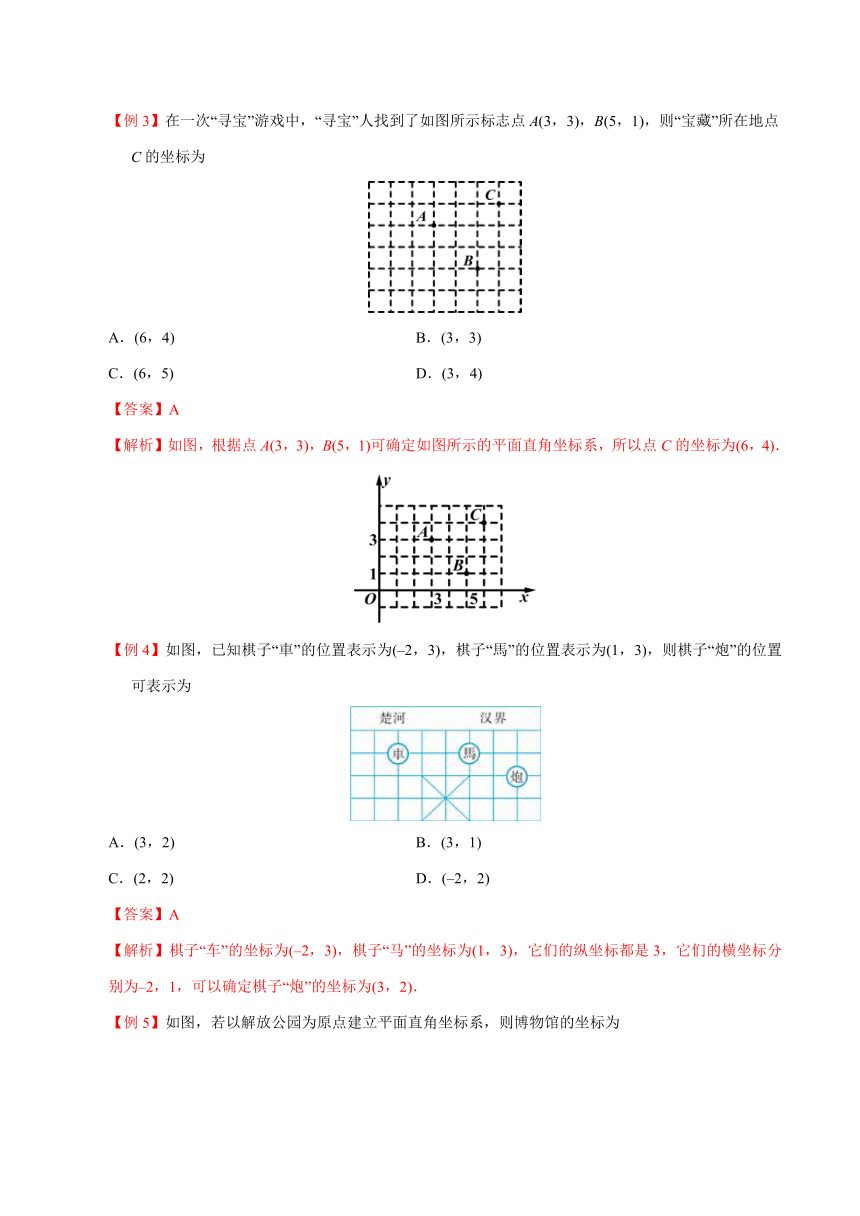
【例2】张强在某旅游景点的动物园的大门口看到这个动物园的平面示意图(如图),若以大门为坐标原点,正东方向为x轴正方向,正北方向为y轴正方向,其他四个景点大致用坐标表示肯定错误的是
A.熊猫馆(1,4) B.猴山(6,0)
C.百鸟园(5,-3) D.驼峰(3,-2)
【答案】C
【解析】若以大门为坐标原点建立直角坐标系,根据各点在坐标系中的位置及坐标的符号,可判定熊猫馆,猴山,百鸟园在第一象限,而驼峰在第四象限,观察各选项可知C选项百鸟园在第四象限,故C错误,故选C.
【例3】在一次“寻宝”游戏中,“寻宝”人找到了如图所示标志点A(3,3),B(5,1),则“宝藏”所在地点C的坐标为
A.(6,4) B.(3,3)
C.(6,5) D.(3,4)
【答案】A
【解析】如图,根据点A(3,3),B(5,1)可确定如图所示的平面直角坐标系,所以点C的坐标为(6,4).
【例4】如图,已知棋子“車”的位置表示为(–2,3),棋子“馬”的位置表示为(1,3),则棋子“炮”的位置可表示为
A.(3,2) B.(3,1)
C.(2,2) D.(–2,2)
【答案】A
【解析】棋子“车”的坐标为(–2,3),棋子“马”的坐标为(1,3),它们的纵坐标都是3,它们的横坐标分别为–2,1,可以确定棋子“炮”的坐标为(3,2).
【例5】如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为
A.(2,3) B.(0,3)
C.(3,2) D.(2,2)
【答案】D
【解析】若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为(2,2).故选D.
【例6】如图是某学校的平面示意图.A,B,C,D,E,F分别表示学校的第1,2,3,4,5,6号楼.
(1)写出A,B,C,D,E的坐标;
(2)位于原点北偏东45°的是哪座楼,它的坐标是多少?
【解析】(1)根据平面直角坐标系得:
A(2,3),B(5,2),C(3,9),D(7,5),E(6,11).
(2)位于原点北偏东45°的点是点F,其坐标为(12,12).
二、用坐标表示平移
1.一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到.
2.对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
3.在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度.
如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或下)平移a个单位长度.
【例7】如图所示,将点A行向右平移3个单位长度,再向下平移5个单位长度,得到;将点B先向下平移5个单位长度,再向右平移3个单位长度,得到;则与相距
A.4个单位长度 B.5个单位长度
C.6个单位长度 D.7个单位长度
【答案】A
【例8】如图所示,点G(–2,–2),将点G先向右平移6个单位长度,再向上平移5个单位长度,得到G′,则G′的坐标为
A.(6,5) B.(4,5)
C.(6,3) D.(4,3)
【答案】D
【解析】本题主要考查了用坐标表示平移.注意左右移动改变点的横坐标,左减右加;上下移动改变点的纵坐标,下减上加.将点G先向右平移6个单位长度,即G′的横坐标为–2+6=4,再向上平移5个单位长度,即G′的纵坐标为–2+5=3,所以G′的坐标为(4,3),故选D.
【例9】将线段AB在坐标系中作平行移动,已知A(-1,2),B(1,1),将线段AB平移后,其两个端点的坐标变为A(-2,1),B(0,0),则它平移的情况是
A.向上平移了1个单位长度,向左平移了1个单位长度
B.向下平移了1个单位长度,向左平移了1个单位长度
C.向下平移了1个单位长度,向右平移了1个单位长度
D.向上平移了1个单位长度,向右平移了1个单位长度
【答案】B
【解析】由点A,B的平移规律可知,此题规律是(x–1,y–1),照此规律可知线段AB向下平移了1个单位长度,向左平移了1个单位长度.故选B.
【名师点睛】本题考查了平移变换,根据左右平移,横坐标变化,纵坐标不变,上下平移,横坐标不变,纵坐标变化,熟记“左减右加,下减上加”是解题关键.
【例10】在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图.
则A20(__________);点A4n的坐标为(__________)(n是正整数).
【答案】10,0;2n,0.
【解析】观察发现,第4次跳动至点的坐标是(2,0),第8次跳动至点的坐标是(4,0),第12次跳动至点的坐标是(6,0),则第4n次跳动至点的坐标是(2n,0),故A20(10,0),故答案为:(10,0);(2n,0).
【例11】将△ABC向右平移4个单位长度,再向下平移5个单位长度,
(1)作出平移后的△A′B′C′;
(2)分别写出A′,B′,C′的坐标.
【解析】(1)如图:
(2)A′(2,0),B′(-1,-7),C′(7,-2).
基础训练
1.下面图形中,射线OP是表示北偏西60°方向的是
A. B.
C. D.
2.将直角坐标系中的点(–1,–3)向上平移4个单位,再向右平移2个单位后的点的坐标为
A.(3,–1) B.(–5,–1)
C.(–3,1) D.(1,1)
3.点 P(–2,–3)向右平移 2 个单位,再向上平移 4 个单位,则所得到的点的坐标为
A.(–2,0) B.(0,–2)
C.(1,0) D.(0,1)
4.课间操时,小明、小丽、小亮的位置如图所示,小明对小亮说:如果我的位置用(0,0)表示,小丽的位置用(2,1)表示,那么你的位置可以表示成
A.(5,4) B.(4,5)
C.(3,4) D.(4,3)
5.如图是小明、小刚、小红做课间操时的位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,那么小红的位置可表示为
A.(1,3) B.(﹣2,3)
C.(–1,3) D.(0,2)
6.中国象棋是中华民族的文化瑰宝,它源远流长,趣味性强,成为极其广泛的棋艺活动.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(–1,–2),“马”位于点(3,–2),则“兵”位于点
A.(–1,1) B.(–2,﹣1)
C.(–3,1) D.(–2,1)
7.火车票上的车次号有两个意义,一是数字越小表示车速越快,1~98次为特快列车,101~198次为直快列车,301~398次为普快列车,401~498次为普客列车;二是单数与双数表示不同的行驶方向,其中单数表示从北京开出,双数表示开往北京,根据以上规定,从武汉开往北京的某一直快列车的车次号可能是
A.200 B.119
C.120 D.319
8.如图,在三角形ABC中,将三角形ABC沿射线BC方向移动,使点B移动到点C,得到三角形DCF,连接AF,若三角形ABC的面积为4,则三角形ACF的面积为
A.2 B.4
C.8 D.16
9.在直角坐标系中,某三角形三个顶点的横坐标不变,纵坐标都增加2个单位长度,则所得三角形与原三角形相比
A.形状不变,面积扩大2倍
B.形状不变,位置向上平移2个单位长度
C.形状不变,位置向右平移2个单位长度
D.以上都不对
10.如图所示的围棋盘放置在某个平面直角坐标系内,如果棋子②的坐标为(-7,-4),棋子④的坐标为(-6,-8),那么棋子①的坐标应该是__________.
11.如图,一艘船在A处遇险后向相距50海里位于B处的救生船报警,用方向和距离描述遇险船相对于救生船的位置__________.
12.已知点A(a,5),B(2,2-b),C(4,2),且AB平行于x轴,AC平行于y轴,则a+b=__________.
13.在平面直角坐标系中,△A′B′C′是由△ABC平移后得到的,△ABC中任意一点P(x0,y0)经过平移后对应点为P′(x0+7,y0+2),若A′的坐标为(5,3),则它的对应的点A的坐标为__________.
14.某飞行监控中心发现某飞机从某个飞机场起飞后沿正南方向飞行100千米,然后向正西方向飞行300千米,又测得该机场的位置位于监控中心的西100千米,北300千米的地方,若以监控中心为坐标原点,以正东、正北方向为x轴、y轴的正方向,请指出该飞机现在的位置__________.(用坐标表示)
15.如图是某中学的平面结构示意图.(图中每个小正方形的边长均为1个单位长度)
(1)在图①中,请以大门为坐标原点,以水平向右为x轴的正方向,以竖直向上为y轴的正方向,用坐标表示下列位置:
实验楼__________、教学楼__________、食堂__________;
(2)在图②中,不以大门为坐标原点,请你建立适当的平面直角坐标系,并写出宿舍楼、实验楼和大门的坐标.
16.在直角坐标系中,△ABC的三个顶点的位置如图所示.
(1)请画出将△ABC先向右平移3个单位,再向上平移1个单位后得△A′B′C′,请在网格纸中画出△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′、B′、C′三点的坐标:A′_____,B′______,C′______.
能力测试
17.如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有
A.2个 B.3个 C.4个 D.5个
18.在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A-…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),D点坐标为(1,3),当蚂蚁爬了2018个单位长度时,它所处位置的坐标为__________.
真题训练
19.(2018?抚顺)已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(–2,1),则点B的对应点的坐标为
A.(5,3) B.(–1,–2)
C.(–1,–1) D.(0,–1)
20.(2018?海南)如图,在平面直角坐标系中,三角形ABC位于第一象限,点A的坐标是(4,3),把三角形ABC向左平移6个单位长度,得到三角形A1B1C1,则点B1的坐标是
A.(–2,3) B.(3,–1)
C.(–3,1) D.(–5,2)
21.(2018?黄石)如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是
A.(–1,6) B.(–9,6)
C.(–1,2) D.(–9,2)
22.(2018?长沙)在平面直角坐标系中,将点A(–2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是__________.
23.(2018?绵阳)如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,–1)和(–3,1),那么“卒”的坐标为__________.
参考答案
1.【答案】A
【解析】根据方向角的定义,射线OP是表示北偏西60°方向可表示为如图,
故选A.
4.【答案】C
【解析】如果小明的位置用(0,0)表示,小丽的位置用(2,1)表示,
如图所示就是以小明为原点的平面直角坐标系,
所以小亮的位置为(3,4).故选C.
5.【答案】C
【解析】根据小明与小刚的位置坐标可建立如图所示直角坐标系,
由图知小红的位置可表示为(–1,3),故选C.
6.【答案】D
【解析】如图所示,根据题意可建立如图所示平面直角坐标系,
则“兵”位于点(–2,1),故选D.
9.【答案】B
【解析】∵三角形三个顶点的横坐标不变,纵坐标都增加2个单位,
∴三角形与原三角形相比,向上平移2个单位,
∴形状不变,位置向上平移2个单位.故选B.
10.【答案】(-3,-7)
【解析】根据棋子②或棋子④的坐标确定坐标原点,从而得出棋子①的坐标.故答案为:(-3,-7).
11.【答案】南偏西15°,50海里
【解析】如图,内错角相等,所以A位于B,南偏西15°,50海里,故答案为:南偏西15°,50海里.
12.【答案】1
【解析】因为AC平行于y轴,所以A,C两点的横坐标相同,即a=4.又AB平行于x轴,所以A,B两点的纵坐标相同,即2-b=5,所以b=-3.所以a+b=1,故答案为:1.
13.【答案】(-2,1)
【解析】根据题意,可得△ABC的平移规律为:向右平移7个单位,向上平移2个单位,∵A′的坐标
为(5,3),∴它对应的点A的坐标为(?2,1),故答案为:(?2,1).
14.【答案】(-400,200)
【解析】该机场的位置位于监控中心的西100千米,北300千米的地方,若以监控中心为坐标原点,则机场的坐标为(-100,300),沿正南方向飞行100千米,然后向正西方向飞行300千米,则飞机现在的位置(-400,200),故答案:(-400,200).
15.【解析】(1)如图1,以大门为坐标原点,以水平向右为x轴的正方向,以竖直向上为y轴的正方向,
实验楼坐标为(2,3)、教学楼的坐标为(4,1)、食堂的坐标为(5,6),故答案为:(2,3)、(4,1)、(5,6).
(2)如图2,以实验楼为坐标原点建立坐标系,
宿舍楼的坐标为(?1,3)、实验楼的坐标为(0,0)、大门的坐标为(?2,?3).
16.【解析】(1)如图所示,△A′B′C′即为所求.
(2)A′(1,4),B′(0,2),C′(4,-1).
17.【答案】B
【解析】由图可知,AB∥x轴,且AB=3,设点C到AB的距离为h,则△ABC的面积=×3h=3,解得h=2,∵点C在第四象限,∴点C的位置如图所示,共有3个,故选B.
18.【答案】(-1,-1)
19.【答案】C
【解析】∵A(1,3)的对应点的坐标为(–2,1),
∴平移规律为横坐标减3,纵坐标减2,
∵点B(2,1)的对应点的坐标为(–1,–1).
故选C.
20.【答案】C
【解析】∵点B的坐标为(3,1),∴向左平移6个单位后,点B1的坐标(–3,1),故选C.
21.【答案】C
【解析】由题意P(–5,4),向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是(–1,2),故选C.
22.【答案】(1,1)
【解析】∵将点A′(–2,3)向右平移3个单位长度,∴得到(1,3),
∵再向下平移2个单位长度,∴平移后对应的点A′的坐标是:(1,1).故答案为:(1,1).
23.【答案】(–2,–2)
【解析】“卒”的坐标为(–2,–2),故答案为:(–2,–2).
7.2 坐标方法的简单应用
知识
1.用坐标表示地理位置
用坐标表示地理位置的过程和方法
(1)建立坐标系,选择一个__________参照点为原点,确定__________的__________.参照点不同,地理位置的坐标也不同.
(2)根据具体问题确定__________.
(3)在坐标平面内画出这些点,并写出各点的__________和各个地点的__________.
2.用坐标表示平移
在平面直角坐标系中,
(1)将点(x,y)向右平移a个单位长度,对应点的横坐标__________a,而纵坐标不变,即坐标变为__________.
(2)将点(x,y)向左平移a个单位长度,对应点的横坐标__________a,而纵坐标不变,即坐标变为__________.
(3)将点(x,y)向下平移a个单位长度,对应点的纵坐标__________a,而横坐标不变,即坐标变为__________.
(4)将点(x,y)向上平移a个单位长度,对应点的纵坐标__________a,而横坐标不变,即坐标变为__________.
3.图形上点的坐标变化与图形平移间的关系
(1)横坐标变化,纵坐标不变:
原图形上的点(x,y)向右平移a个单位
原图形上的点(x,y)向左平移a个单位
(2)横坐标不变,纵坐标变化:
原图形上的点(x,y)向上平移b个单位
原图形上的点(x,y)向下平移b个单位
(3)横坐标、纵坐标都变化:
原图形上的点(x,y)向右平移a个单位,向上平移b个单位
原图形上的点(x,y)向右平移a个单位,向下平移b个单位
原图形上的点(x,y)向左平移a个单位,向上平移b个单位
原图形上的点(x,y)向左平移a个单位,向下平移b个单位
知识参考答案:
1.(1)适当的,x轴和y轴,正方向(2)单位长度(3)坐标,名称2.(1)加上,(x+a,y)(2)减去,(x-a,y)(3)减去,(x,y-a)(4)加上,(x,y+a)
重点
重点
建立适当的平面直角坐标系表示地理位置,掌握坐标变化与图形平移的关系,利用坐标变化与图形平移的关系解决实际问题
难点
建立适当的平面直角坐标系,平面直角坐标系中,点的平移与图形的平移的关系
易错
混淆点的坐标的平移规律
一、用坐标表示地理位置
1.确定坐标原点
用坐标表示地理位置时,要注意选择适当的位置为坐标原点,这里所说的适当,通常要么是比较有名的地点,要么是所要绘制的区域内较居中的位置.不同的原点产生的地理位置的坐标也不同.原点不同,地理位置的坐标也不同.用适当的位置表示原点,可以降低计算的难度.
2.如何确定x轴与y轴的方向
坐标轴的方向通常是选择以水平线为x轴,以向右为正方向(正东),以竖直线为y轴,以向上为正方向(正北),这样可以使东西南北的方向与地理位置的方向保持一致.
【例1】如图,是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为
A.(2,3),(3,2) B.(3,2),(2,3)
C.(2,3),(-3,2) D.(3,2),(-2,3)
【答案】D
【解析】建立平面直角坐标系如图,点B(3,2),D(?2,3),故选D.
【例2】张强在某旅游景点的动物园的大门口看到这个动物园的平面示意图(如图),若以大门为坐标原点,正东方向为x轴正方向,正北方向为y轴正方向,其他四个景点大致用坐标表示肯定错误的是
A.熊猫馆(1,4) B.猴山(6,0)
C.百鸟园(5,-3) D.驼峰(3,-2)
【答案】C
【解析】若以大门为坐标原点建立直角坐标系,根据各点在坐标系中的位置及坐标的符号,可判定熊猫馆,猴山,百鸟园在第一象限,而驼峰在第四象限,观察各选项可知C选项百鸟园在第四象限,故C错误,故选C.
【例3】在一次“寻宝”游戏中,“寻宝”人找到了如图所示标志点A(3,3),B(5,1),则“宝藏”所在地点C的坐标为
A.(6,4) B.(3,3)
C.(6,5) D.(3,4)
【答案】A
【解析】如图,根据点A(3,3),B(5,1)可确定如图所示的平面直角坐标系,所以点C的坐标为(6,4).
【例4】如图,已知棋子“車”的位置表示为(–2,3),棋子“馬”的位置表示为(1,3),则棋子“炮”的位置可表示为
A.(3,2) B.(3,1)
C.(2,2) D.(–2,2)
【答案】A
【解析】棋子“车”的坐标为(–2,3),棋子“马”的坐标为(1,3),它们的纵坐标都是3,它们的横坐标分别为–2,1,可以确定棋子“炮”的坐标为(3,2).
【例5】如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为
A.(2,3) B.(0,3)
C.(3,2) D.(2,2)
【答案】D
【解析】若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为(2,2).故选D.
【例6】如图是某学校的平面示意图.A,B,C,D,E,F分别表示学校的第1,2,3,4,5,6号楼.
(1)写出A,B,C,D,E的坐标;
(2)位于原点北偏东45°的是哪座楼,它的坐标是多少?
【解析】(1)根据平面直角坐标系得:
A(2,3),B(5,2),C(3,9),D(7,5),E(6,11).
(2)位于原点北偏东45°的点是点F,其坐标为(12,12).
二、用坐标表示平移
1.一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到.
2.对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
3.在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度.
如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或下)平移a个单位长度.
【例7】如图所示,将点A行向右平移3个单位长度,再向下平移5个单位长度,得到;将点B先向下平移5个单位长度,再向右平移3个单位长度,得到;则与相距
A.4个单位长度 B.5个单位长度
C.6个单位长度 D.7个单位长度
【答案】A
【例8】如图所示,点G(–2,–2),将点G先向右平移6个单位长度,再向上平移5个单位长度,得到G′,则G′的坐标为
A.(6,5) B.(4,5)
C.(6,3) D.(4,3)
【答案】D
【解析】本题主要考查了用坐标表示平移.注意左右移动改变点的横坐标,左减右加;上下移动改变点的纵坐标,下减上加.将点G先向右平移6个单位长度,即G′的横坐标为–2+6=4,再向上平移5个单位长度,即G′的纵坐标为–2+5=3,所以G′的坐标为(4,3),故选D.
【例9】将线段AB在坐标系中作平行移动,已知A(-1,2),B(1,1),将线段AB平移后,其两个端点的坐标变为A(-2,1),B(0,0),则它平移的情况是
A.向上平移了1个单位长度,向左平移了1个单位长度
B.向下平移了1个单位长度,向左平移了1个单位长度
C.向下平移了1个单位长度,向右平移了1个单位长度
D.向上平移了1个单位长度,向右平移了1个单位长度
【答案】B
【解析】由点A,B的平移规律可知,此题规律是(x–1,y–1),照此规律可知线段AB向下平移了1个单位长度,向左平移了1个单位长度.故选B.
【名师点睛】本题考查了平移变换,根据左右平移,横坐标变化,纵坐标不变,上下平移,横坐标不变,纵坐标变化,熟记“左减右加,下减上加”是解题关键.
【例10】在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图.
则A20(__________);点A4n的坐标为(__________)(n是正整数).
【答案】10,0;2n,0.
【解析】观察发现,第4次跳动至点的坐标是(2,0),第8次跳动至点的坐标是(4,0),第12次跳动至点的坐标是(6,0),则第4n次跳动至点的坐标是(2n,0),故A20(10,0),故答案为:(10,0);(2n,0).
【例11】将△ABC向右平移4个单位长度,再向下平移5个单位长度,
(1)作出平移后的△A′B′C′;
(2)分别写出A′,B′,C′的坐标.
【解析】(1)如图:
(2)A′(2,0),B′(-1,-7),C′(7,-2).
基础训练
1.下面图形中,射线OP是表示北偏西60°方向的是
A. B.
C. D.
2.将直角坐标系中的点(–1,–3)向上平移4个单位,再向右平移2个单位后的点的坐标为
A.(3,–1) B.(–5,–1)
C.(–3,1) D.(1,1)
3.点 P(–2,–3)向右平移 2 个单位,再向上平移 4 个单位,则所得到的点的坐标为
A.(–2,0) B.(0,–2)
C.(1,0) D.(0,1)
4.课间操时,小明、小丽、小亮的位置如图所示,小明对小亮说:如果我的位置用(0,0)表示,小丽的位置用(2,1)表示,那么你的位置可以表示成
A.(5,4) B.(4,5)
C.(3,4) D.(4,3)
5.如图是小明、小刚、小红做课间操时的位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,那么小红的位置可表示为
A.(1,3) B.(﹣2,3)
C.(–1,3) D.(0,2)
6.中国象棋是中华民族的文化瑰宝,它源远流长,趣味性强,成为极其广泛的棋艺活动.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(–1,–2),“马”位于点(3,–2),则“兵”位于点
A.(–1,1) B.(–2,﹣1)
C.(–3,1) D.(–2,1)
7.火车票上的车次号有两个意义,一是数字越小表示车速越快,1~98次为特快列车,101~198次为直快列车,301~398次为普快列车,401~498次为普客列车;二是单数与双数表示不同的行驶方向,其中单数表示从北京开出,双数表示开往北京,根据以上规定,从武汉开往北京的某一直快列车的车次号可能是
A.200 B.119
C.120 D.319
8.如图,在三角形ABC中,将三角形ABC沿射线BC方向移动,使点B移动到点C,得到三角形DCF,连接AF,若三角形ABC的面积为4,则三角形ACF的面积为
A.2 B.4
C.8 D.16
9.在直角坐标系中,某三角形三个顶点的横坐标不变,纵坐标都增加2个单位长度,则所得三角形与原三角形相比
A.形状不变,面积扩大2倍
B.形状不变,位置向上平移2个单位长度
C.形状不变,位置向右平移2个单位长度
D.以上都不对
10.如图所示的围棋盘放置在某个平面直角坐标系内,如果棋子②的坐标为(-7,-4),棋子④的坐标为(-6,-8),那么棋子①的坐标应该是__________.
11.如图,一艘船在A处遇险后向相距50海里位于B处的救生船报警,用方向和距离描述遇险船相对于救生船的位置__________.
12.已知点A(a,5),B(2,2-b),C(4,2),且AB平行于x轴,AC平行于y轴,则a+b=__________.
13.在平面直角坐标系中,△A′B′C′是由△ABC平移后得到的,△ABC中任意一点P(x0,y0)经过平移后对应点为P′(x0+7,y0+2),若A′的坐标为(5,3),则它的对应的点A的坐标为__________.
14.某飞行监控中心发现某飞机从某个飞机场起飞后沿正南方向飞行100千米,然后向正西方向飞行300千米,又测得该机场的位置位于监控中心的西100千米,北300千米的地方,若以监控中心为坐标原点,以正东、正北方向为x轴、y轴的正方向,请指出该飞机现在的位置__________.(用坐标表示)
15.如图是某中学的平面结构示意图.(图中每个小正方形的边长均为1个单位长度)
(1)在图①中,请以大门为坐标原点,以水平向右为x轴的正方向,以竖直向上为y轴的正方向,用坐标表示下列位置:
实验楼__________、教学楼__________、食堂__________;
(2)在图②中,不以大门为坐标原点,请你建立适当的平面直角坐标系,并写出宿舍楼、实验楼和大门的坐标.
16.在直角坐标系中,△ABC的三个顶点的位置如图所示.
(1)请画出将△ABC先向右平移3个单位,再向上平移1个单位后得△A′B′C′,请在网格纸中画出△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′、B′、C′三点的坐标:A′_____,B′______,C′______.
能力测试
17.如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有
A.2个 B.3个 C.4个 D.5个
18.在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A-…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),D点坐标为(1,3),当蚂蚁爬了2018个单位长度时,它所处位置的坐标为__________.
真题训练
19.(2018?抚顺)已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(–2,1),则点B的对应点的坐标为
A.(5,3) B.(–1,–2)
C.(–1,–1) D.(0,–1)
20.(2018?海南)如图,在平面直角坐标系中,三角形ABC位于第一象限,点A的坐标是(4,3),把三角形ABC向左平移6个单位长度,得到三角形A1B1C1,则点B1的坐标是
A.(–2,3) B.(3,–1)
C.(–3,1) D.(–5,2)
21.(2018?黄石)如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是
A.(–1,6) B.(–9,6)
C.(–1,2) D.(–9,2)
22.(2018?长沙)在平面直角坐标系中,将点A(–2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是__________.
23.(2018?绵阳)如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,–1)和(–3,1),那么“卒”的坐标为__________.
参考答案
1.【答案】A
【解析】根据方向角的定义,射线OP是表示北偏西60°方向可表示为如图,
故选A.
4.【答案】C
【解析】如果小明的位置用(0,0)表示,小丽的位置用(2,1)表示,
如图所示就是以小明为原点的平面直角坐标系,
所以小亮的位置为(3,4).故选C.
5.【答案】C
【解析】根据小明与小刚的位置坐标可建立如图所示直角坐标系,
由图知小红的位置可表示为(–1,3),故选C.
6.【答案】D
【解析】如图所示,根据题意可建立如图所示平面直角坐标系,
则“兵”位于点(–2,1),故选D.
9.【答案】B
【解析】∵三角形三个顶点的横坐标不变,纵坐标都增加2个单位,
∴三角形与原三角形相比,向上平移2个单位,
∴形状不变,位置向上平移2个单位.故选B.
10.【答案】(-3,-7)
【解析】根据棋子②或棋子④的坐标确定坐标原点,从而得出棋子①的坐标.故答案为:(-3,-7).
11.【答案】南偏西15°,50海里
【解析】如图,内错角相等,所以A位于B,南偏西15°,50海里,故答案为:南偏西15°,50海里.
12.【答案】1
【解析】因为AC平行于y轴,所以A,C两点的横坐标相同,即a=4.又AB平行于x轴,所以A,B两点的纵坐标相同,即2-b=5,所以b=-3.所以a+b=1,故答案为:1.
13.【答案】(-2,1)
【解析】根据题意,可得△ABC的平移规律为:向右平移7个单位,向上平移2个单位,∵A′的坐标
为(5,3),∴它对应的点A的坐标为(?2,1),故答案为:(?2,1).
14.【答案】(-400,200)
【解析】该机场的位置位于监控中心的西100千米,北300千米的地方,若以监控中心为坐标原点,则机场的坐标为(-100,300),沿正南方向飞行100千米,然后向正西方向飞行300千米,则飞机现在的位置(-400,200),故答案:(-400,200).
15.【解析】(1)如图1,以大门为坐标原点,以水平向右为x轴的正方向,以竖直向上为y轴的正方向,
实验楼坐标为(2,3)、教学楼的坐标为(4,1)、食堂的坐标为(5,6),故答案为:(2,3)、(4,1)、(5,6).
(2)如图2,以实验楼为坐标原点建立坐标系,
宿舍楼的坐标为(?1,3)、实验楼的坐标为(0,0)、大门的坐标为(?2,?3).
16.【解析】(1)如图所示,△A′B′C′即为所求.
(2)A′(1,4),B′(0,2),C′(4,-1).
17.【答案】B
【解析】由图可知,AB∥x轴,且AB=3,设点C到AB的距离为h,则△ABC的面积=×3h=3,解得h=2,∵点C在第四象限,∴点C的位置如图所示,共有3个,故选B.
18.【答案】(-1,-1)
19.【答案】C
【解析】∵A(1,3)的对应点的坐标为(–2,1),
∴平移规律为横坐标减3,纵坐标减2,
∵点B(2,1)的对应点的坐标为(–1,–1).
故选C.
20.【答案】C
【解析】∵点B的坐标为(3,1),∴向左平移6个单位后,点B1的坐标(–3,1),故选C.
21.【答案】C
【解析】由题意P(–5,4),向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是(–1,2),故选C.
22.【答案】(1,1)
【解析】∵将点A′(–2,3)向右平移3个单位长度,∴得到(1,3),
∵再向下平移2个单位长度,∴平移后对应的点A′的坐标是:(1,1).故答案为:(1,1).
23.【答案】(–2,–2)
【解析】“卒”的坐标为(–2,–2),故答案为:(–2,–2).
