11.1.2 三角形的高、中线与角平分线(解析版)同步练习
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线(解析版)同步练习 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-26 00:00:00 | ||
图片预览


文档简介
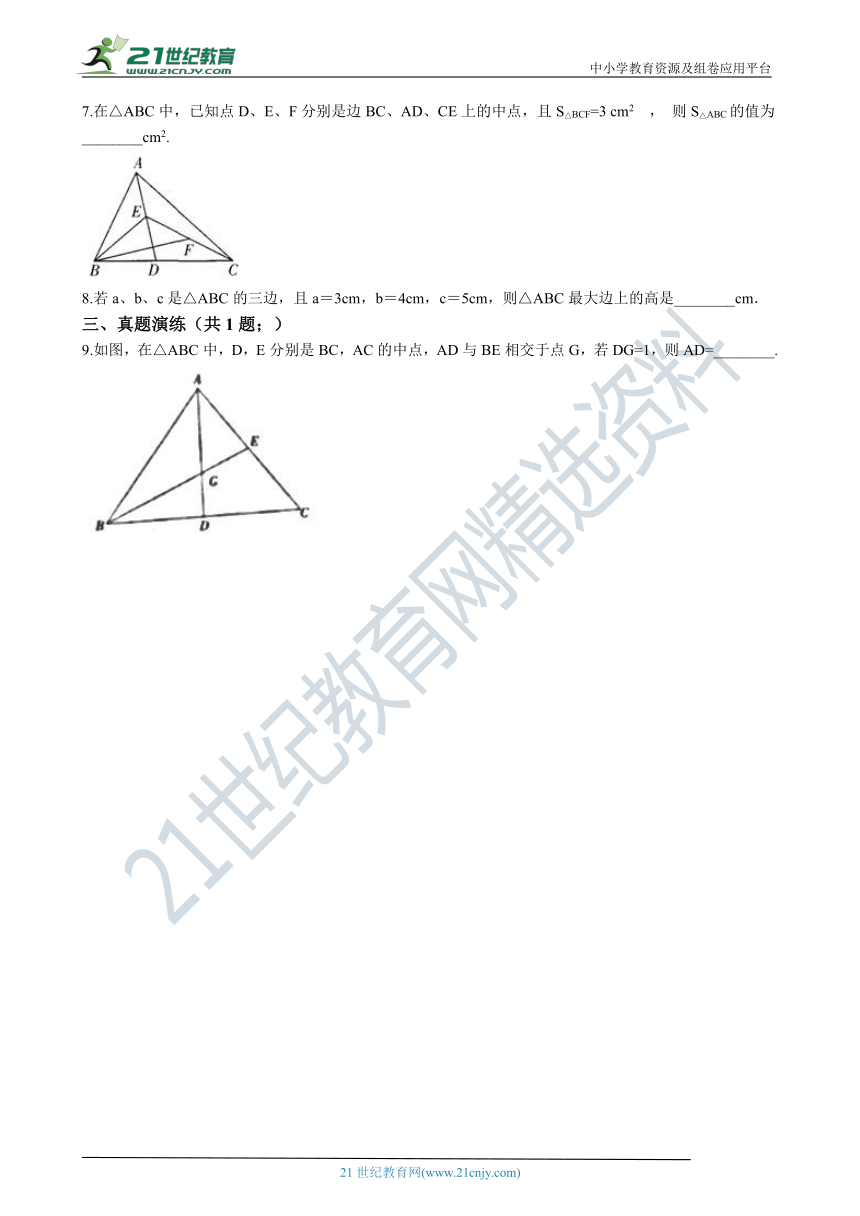
初中数学八年级上学期第十一章11.1.2 三角形的高、中线与角平分线
一、基础巩固(共4题;)
1.三角形一边上的中线把原三角形一定分成两个( ??)
A.?形状相同的三角形????????????B.?面积相等的三角形????????????C.?直角三角形????????????D.?周长相等的三角形
2.画△ABC中AC边上的高,下列四个画法中正确的是(? ? )
A.?????????B.?????????C.?????????D.?
3.用三角板作△ABC 边 BC 上的高,下列三角板的摆放位置正确的是(???????? ).
A.??????????B.? C.????? ?D.?.
4.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′. 21教育网
①在给定方格纸中画出平移后的△A′B′C′;
②画出AB边上的中线CD
③画出BC边上的高线AE________
④点 F为方格纸上的格点(异于点B ),若 ,则图中的格点F 共有________个.
二、强化提升(共4题;)
5.G为△ABC的重心,△ABC的三边长满足AB>BC>CA,记△GAB,△GBC,△GCA的面积分别为S1、S2、S3 , 则有(?? ) 21cnjy.com
A.?S1>S2>S3??????????? ??B.?S1=S2=S3????????? ????C.?S1<S2<S3????? ????????D.?S1、S2、S3的大小关系不确定
6.如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE.若BD=3,CE=2,则△ABC的面积为(? ? ) 21·cn·jy·com
A.?4??????????????????????????????????????????B.?8??????????????????????????????????????????C.?12??????????????????????????????????????????D.?16
7.在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△BCF=3 cm2 , 则S△ABC的值为________cm2. www.21-cn-jy.com
8.若a、b、c是△ABC的三边,且a=3cm,b=4cm,c=5cm,则△ABC最大边上的高是________cm.
三、真题演练(共1题;)
9.如图,在△ABC中,D,E分别是BC,AC的中点,AD与BE相交于点G,若DG=1,则AD=________.
答案解析部分
一、基础巩固
1. B
解:三角形一边上的中线把原三角形一定分成两个面积相等的三角形. 故答案为:B. 【分析】根据等底同高的两个三角形的面积相等可求解。
2. C
解:A选项根据图形可知做的BC边上的高,不符合题意;
B选项做三角形的高必须过其中一个顶点向对边引垂线,不符合题意;
C选项,钝角三角形,延长CA,过点B向CA的延长线引垂线即为高,符合题意;
D选项根据图形可知做的AB边上的高,不符合题意。
故答案为:C
【分析】根据三角形高的定义:从三角形的一个顶点向它的对边所在的直线做垂线,顶点到垂足之间的线段叫做三角形的高线;要作△ABC中AC边上的高,就是过点B作AC边的垂线段,可得出正确的选项。
3. A
解:A、 作法符合题意,故A符合题意,
B 、没有过BC边所对的顶点,作法不符合题意,故B不符合题意.
C 、没有垂直BC , 不符合题意,故C不符合题意.
D、 是作AC的高,不是作BC的高,不符合题意,故D不符合题意.
故答案为:A. 【分析】根据三角形上作高的定义,从三角形一个顶点向它的对边作一条垂线,垂线顶点和垂足之间的线段称三角形这条边上的高,进行判断即可。·c·n·j·y
4. 解:如图,△A′B′C′、线段CD、线段AE即为所求;
;7
【分析】(1)观察B与B'两点的位置得出平移方向和距离:将点B向左平移7个单位,向下平移一个单位,利用方格纸的特点及平移的性质,将点A,C也作相同的平移即可得出其对应点A',C'再顺次连接即可得出所求的△ A′B′C′; (2)利用方格纸的特点,把AB看成一个长为6,宽为4的矩形的对角线,根据矩形的对角线互相平分即可找出AB的中点D,再连接CD, 线段CD 就是所求的 AB边上的中线 ; (3)利用方格纸的特点及三角形高线的定义,过点A的水平线与BC所在的竖直线相交于点E, 线段AE就是 BC边上的高线 ; (4)根据同底等高的三角形的三角形的面积相等,故点F只要在过点B且与AC平行的直线上即可,利用方格纸的特点即可得出答案。21·世纪*教育网
二、强化提升
5. B
解:如图,延长CG交AB于点D
则△ACD的面积=△BCD的面积,△AGD的面积=△BGD的面积
∴S2=S3同理可证明S1=S2
∴S1=S2=S3
故答案为:B. 【分析】如图,延长CG交AB于点D,根据等底同高的两个三角形的面积相等,得三角形的任意一条中线将三角形分成两个面积相等的三角形,故△ACD的面积=△BCD的面积,△AGD的面积=△BGD的面积,根据等式的性质得出S2=S3,同理可证明S1=S2,故S1=S2=S3。【来源:21·世纪·教育·网】
6. A
解:∵BD,CE分别为AC,AB边上的中线,
∴点O是△ABC的重心,
∴OC= =
∴S△BDC= =2
∵BD为AC边上的中线
∴△ABC的面积=2S△BDC=4,
故答案为:A. 【分析】由三角形重心的定义可知点O是△ABC的重心,由三角形的重心的性质可得OC= , 再根据三角形的面积公式和已知条件可求得S△BDC= BD.OC,所以S△ABC=2S△BDC可求解。
7. 12
解:∵点E是AD的中点,
∴S△ABE= S△ABD , S△ACE= S△ADC ,
∴S△ABE+S△ACE= S△ABC ,
∴S△BCE= S△ABC ,
∵点F是CE的中点,
∴S△BEF= S△BCE= S△ABC ,
又∵S△BCF=3cm2 ,
∴S△ABC=4S△BEF=12 cm2.
故答案是:12. 【分析】三角形的中线把三角形分成面积相等的两部分,据此解答即可.
8. 2.4cm
解:∵a=3cm,b=4cm,c=5cm,
∴△ABC是直角三角形,
∵S△ABC=3×4÷2=6cm2 ,
∴S△ABC=5×最大边上的高=12,
∴△ABC最大边上的高是2.4cm.
故答案为:2.4 cm 【分析】根据三角形的三边关系可得,该三角形为直角三角形,根据三角形的面积公式,求出高即可。-y
三、真题演练
9. 3
解:∵D、E是BC、AC的中点 ∴G点为△ABC的重心
可得出AG=2DG=2, 所以AD=AG+DG=2+1=3 【分析】利用三角形的重心的性质,可得出AG,求得AD的长。www-2-1-cnjy-com
一、基础巩固(共4题;)
1.三角形一边上的中线把原三角形一定分成两个( ??)
A.?形状相同的三角形????????????B.?面积相等的三角形????????????C.?直角三角形????????????D.?周长相等的三角形
2.画△ABC中AC边上的高,下列四个画法中正确的是(? ? )
A.?????????B.?????????C.?????????D.?
3.用三角板作△ABC 边 BC 上的高,下列三角板的摆放位置正确的是(???????? ).
A.??????????B.? C.????? ?D.?.
4.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′. 21教育网
①在给定方格纸中画出平移后的△A′B′C′;
②画出AB边上的中线CD
③画出BC边上的高线AE________
④点 F为方格纸上的格点(异于点B ),若 ,则图中的格点F 共有________个.
二、强化提升(共4题;)
5.G为△ABC的重心,△ABC的三边长满足AB>BC>CA,记△GAB,△GBC,△GCA的面积分别为S1、S2、S3 , 则有(?? ) 21cnjy.com
A.?S1>S2>S3??????????? ??B.?S1=S2=S3????????? ????C.?S1<S2<S3????? ????????D.?S1、S2、S3的大小关系不确定
6.如图,在△ABC中,BD,CE分别为AC,AB边上的中线,BD⊥CE.若BD=3,CE=2,则△ABC的面积为(? ? ) 21·cn·jy·com
A.?4??????????????????????????????????????????B.?8??????????????????????????????????????????C.?12??????????????????????????????????????????D.?16
7.在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△BCF=3 cm2 , 则S△ABC的值为________cm2. www.21-cn-jy.com
8.若a、b、c是△ABC的三边,且a=3cm,b=4cm,c=5cm,则△ABC最大边上的高是________cm.
三、真题演练(共1题;)
9.如图,在△ABC中,D,E分别是BC,AC的中点,AD与BE相交于点G,若DG=1,则AD=________.
答案解析部分
一、基础巩固
1. B
解:三角形一边上的中线把原三角形一定分成两个面积相等的三角形. 故答案为:B. 【分析】根据等底同高的两个三角形的面积相等可求解。
2. C
解:A选项根据图形可知做的BC边上的高,不符合题意;
B选项做三角形的高必须过其中一个顶点向对边引垂线,不符合题意;
C选项,钝角三角形,延长CA,过点B向CA的延长线引垂线即为高,符合题意;
D选项根据图形可知做的AB边上的高,不符合题意。
故答案为:C
【分析】根据三角形高的定义:从三角形的一个顶点向它的对边所在的直线做垂线,顶点到垂足之间的线段叫做三角形的高线;要作△ABC中AC边上的高,就是过点B作AC边的垂线段,可得出正确的选项。
3. A
解:A、 作法符合题意,故A符合题意,
B 、没有过BC边所对的顶点,作法不符合题意,故B不符合题意.
C 、没有垂直BC , 不符合题意,故C不符合题意.
D、 是作AC的高,不是作BC的高,不符合题意,故D不符合题意.
故答案为:A. 【分析】根据三角形上作高的定义,从三角形一个顶点向它的对边作一条垂线,垂线顶点和垂足之间的线段称三角形这条边上的高,进行判断即可。·c·n·j·y
4. 解:如图,△A′B′C′、线段CD、线段AE即为所求;
;7
【分析】(1)观察B与B'两点的位置得出平移方向和距离:将点B向左平移7个单位,向下平移一个单位,利用方格纸的特点及平移的性质,将点A,C也作相同的平移即可得出其对应点A',C'再顺次连接即可得出所求的△ A′B′C′; (2)利用方格纸的特点,把AB看成一个长为6,宽为4的矩形的对角线,根据矩形的对角线互相平分即可找出AB的中点D,再连接CD, 线段CD 就是所求的 AB边上的中线 ; (3)利用方格纸的特点及三角形高线的定义,过点A的水平线与BC所在的竖直线相交于点E, 线段AE就是 BC边上的高线 ; (4)根据同底等高的三角形的三角形的面积相等,故点F只要在过点B且与AC平行的直线上即可,利用方格纸的特点即可得出答案。21·世纪*教育网
二、强化提升
5. B
解:如图,延长CG交AB于点D
则△ACD的面积=△BCD的面积,△AGD的面积=△BGD的面积
∴S2=S3同理可证明S1=S2
∴S1=S2=S3
故答案为:B. 【分析】如图,延长CG交AB于点D,根据等底同高的两个三角形的面积相等,得三角形的任意一条中线将三角形分成两个面积相等的三角形,故△ACD的面积=△BCD的面积,△AGD的面积=△BGD的面积,根据等式的性质得出S2=S3,同理可证明S1=S2,故S1=S2=S3。【来源:21·世纪·教育·网】
6. A
解:∵BD,CE分别为AC,AB边上的中线,
∴点O是△ABC的重心,
∴OC= =
∴S△BDC= =2
∵BD为AC边上的中线
∴△ABC的面积=2S△BDC=4,
故答案为:A. 【分析】由三角形重心的定义可知点O是△ABC的重心,由三角形的重心的性质可得OC= , 再根据三角形的面积公式和已知条件可求得S△BDC= BD.OC,所以S△ABC=2S△BDC可求解。
7. 12
解:∵点E是AD的中点,
∴S△ABE= S△ABD , S△ACE= S△ADC ,
∴S△ABE+S△ACE= S△ABC ,
∴S△BCE= S△ABC ,
∵点F是CE的中点,
∴S△BEF= S△BCE= S△ABC ,
又∵S△BCF=3cm2 ,
∴S△ABC=4S△BEF=12 cm2.
故答案是:12. 【分析】三角形的中线把三角形分成面积相等的两部分,据此解答即可.
8. 2.4cm
解:∵a=3cm,b=4cm,c=5cm,
∴△ABC是直角三角形,
∵S△ABC=3×4÷2=6cm2 ,
∴S△ABC=5×最大边上的高=12,
∴△ABC最大边上的高是2.4cm.
故答案为:2.4 cm 【分析】根据三角形的三边关系可得,该三角形为直角三角形,根据三角形的面积公式,求出高即可。-y
三、真题演练
9. 3
解:∵D、E是BC、AC的中点 ∴G点为△ABC的重心
可得出AG=2DG=2, 所以AD=AG+DG=2+1=3 【分析】利用三角形的重心的性质,可得出AG,求得AD的长。www-2-1-cnjy-com
