11.2.1 三角形的内角(解析版)同步练习
文档属性
| 名称 | 11.2.1 三角形的内角(解析版)同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-26 00:00:00 | ||
图片预览



文档简介
初中数学人教版八年级上学期 第十一章 11.2.1 三角形的内角
一、基础巩固(共3题;)
1.己知钝角△ABC中,∠A=30°,则下列结论正确的是( ??)
A.?0°<∠B<60°???????????B.?90°<∠B<150°???????????C.?0°<∠B<60°或90°<∠B<150°???????????D.?以上都不对
2.适合条件∠A= =∠B= =∠C的△ABC是(? ? )
A.?锐角三角形???????????????????????B.?直角三角形???????????????????????C.?钝角三角形???????????????????????D.?等边三角形
3.将一把直尺与一块含30°和60°角的三角板ABC按如图所示的位置放置,直尺的一边恰好经过点A,如果∠CDE=50°,那么∠BAF的度数为( ??) 2-1-c-n-j-y
A.?15°???????????????????????????????????????B.?20°???????????????????????????????????????C.?30°???????????????????????????????????????D.?40°
二、强化提升(共6题;)
4.如图,直线 ,若 , ,则 的大小为(??? )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
5.如图,公园A在公园B的北偏东50°方向,公园C在公园B的北偏西25°方向,若A,B两公园到公园C的两直线的夹角∠C为35°,那么公园C在公园A的( ??) 21*cnjy*com
A.?西北方向??????????????????B.?北偏西60°方向??????????????????C.?北偏西70°方向??????????????????D.?南偏东75°方向
6.已知三角形ABC的三个内角满足关系∠B+∠C=3∠A,则此三角形(?? ?).
A.?一定有一个内角为45°?????B.?一定有一个内角为60°?????C.?一定是直角三角形?????D.?一定是钝角三角形
7.如图,在△ABC中,OB,OC分别为∠ABC和∠ACB的平分线,且∠A=70°,则∠BOC=________.
8.如图,AB∥CD,过直线EF上的点G作GH⊥AB,若∠1=50°,则∠2=________°。
第7题图 第8题图
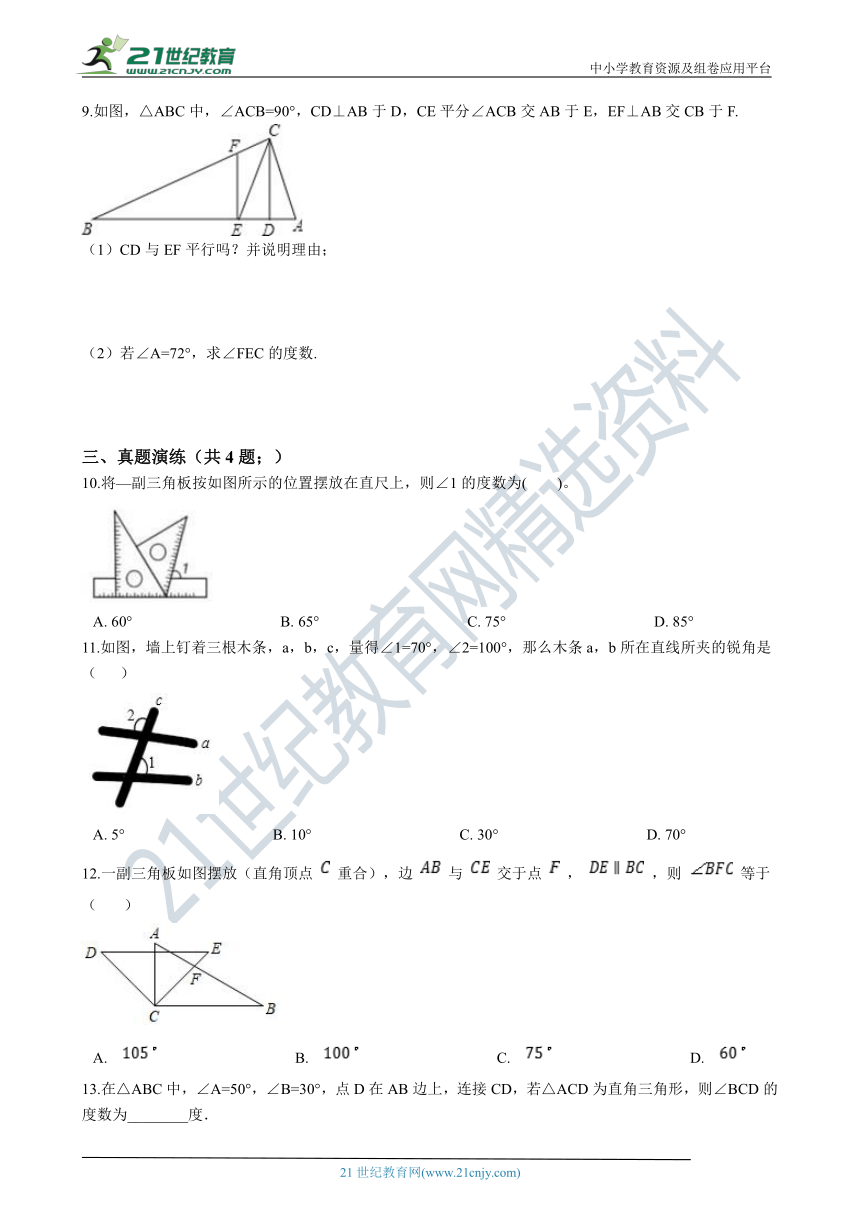
9.如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
(1)CD与EF平行吗?并说明理由;
(2)若∠A=72°,求∠FEC的度数.
三、真题演练(共4题;)
10.将—副三角板按如图所示的位置摆放在直尺上,则∠1的度数为(?? ?? )。
A.?60°???????????????????????????????????????B.?65°???????????????????????????????????????C.?75°???????????????????????????????????????D.?85°
11.如图,墙上钉着三根木条,a,b,c,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角是( ??) 21·cn·jy·com
A.?5°???????????????????????????????????????B.?10°???????????????????????????????????????C.?30°???????????????????????????????????????D.?70°
12.一副三角板如图摆放(直角顶点 重合),边 与 交于点 , ,则 等于(?? ? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
13.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为________度. 【来源:21cnj*y.co*m】
答案解析部分
一、基础巩固
1. C
解:∵∠A+∠B+∠C=180°,∠B=30° ∴∠B+∠C=150° ∵△ABC是钝角三角形 ∴ 0°<∠B<60°或90°<∠B<150° , 故答案为:C 【分析】根据三角形内角和定理,就可求出∠B+∠C的值,再根据钝角三角形的定义,就可求出∠B的度数的取值范围。21cnjy.com
2. B
解:∵∠A= ∠B= ∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180 ?,即6∠A=180 ?,
∴∠A=30 ? ,
∴∠B=60 ? ,∠C=90 ? ,
∴△ABC为直角三角形.
故答案为:B. 【分析】由已知条件可得∠B=2∠A,∠C=3∠A,再根据三角形的内角和定理可得关于∠A的方程,解方程可求得各角的度数,由角的度数即可判断三角形的形状。www-2-1-cnjy-com
3. B
解:由图可得,∠CDE=50°,∠C=90°,
∴∠CED=40°,
又∵DE∥AF,
∴∠CAF=40°,
∵∠BAC=60°,
∴∠BAF=60°﹣40°=20°,
故答案为:B.
【分析】根据三角形的内角和定理可求出∠CED的度数,根据两直线平行,同位角相等可求出∠CAF的度数,利用角的和差关系求出∠BAF的度数.www.21-cn-jy.com
二、强化提升
4. C
解:如图,
∵l1∥l2 ,
∴∠1=∠4=72°,
∵∠2+∠3+∠4=180°,
∴∠2=180°-∠3-∠4=180°-50°-72°=58°,
故答案为:C. 【分析】根据两直线平行内错角相等,可得∠1=∠4=72°,利用三角形内角和定理可求出∠2的度数.
5. B
解:如图, 由题意得BD∥EF,∠CBA=50°+25°=75°, ∴∠BAE=∠DBA=50°, 在△ABC中,∠CAB=180°-∠C-∠CBA=70°, ∴∠CAF=180°-∠CAB-∠BAE=60°, ∴ 公园C在公园A的北偏西60°方向. 21世纪教育网版权所有
故答案为:B.
【分析】根据两直线平行内错角相等,可得∠BAE=∠DBA=50°,利用三角形内角和定理求出∠CAB的度数,利用平角的定义可求出∠CAF的度数,从而可求出结论.1教育网
6. A
解:∵∠A+∠B+∠C=180°,
∴∠B+∠C=180°-∠A,
又∵∠B+∠C=3∠A,
∴3∠A=180°-∠A,
∴∠A=45°.
故答案为:A.
【分析】根据三角形的内角和定理得出∠B+∠C=180°-∠A,又 ∠B+∠C=3∠A 从而列出方程求出∠A的度数,即可得出答案。2·1·c·n·j·y
7. 125°
解:∵∠A=70°,∠A+∠ABC+∠ACB=180°
∴∠ABC+∠ACB=110°
∵OB、OC分别平分∠ABC和∠ACB
∴∠OBC= ∠ABC,∠OCB= ∠ACB,
∴∠OBC+∠OCB= (∠ABC+∠ACB)=55°
∵∠BPC+∠PBC+∠PCB=180°
∴∠BPC=125°
故答案为:125°
【分析】利用三角形内角和定理求出∠ABC+∠ACB的值,再利用角平分线的定义求出∠OBC+∠OCB的值,然后利用三角形内角和定理,在△BOC中求出∠BOC的度数。【来源:21·世纪·教育·网】
8. 40
解: ∵ ∠1=50°?,∴∠3=50°, AB∥CD,∴∠4=∠3=50°, GH⊥AB,∠GHA=90°, ∠2=90°-50°=40°。【出处:21教育名师】
【分析】由两直线平行可知同位角相等,再根据直角三角形中两锐角互余即可。
9. (1)解:∵? CD⊥AB,EF⊥AB,
∴ ∠CDB=∠FEB=90°,
∴? EF∥CD; (2)解:∵∠ ACB=90°,CE平分∠ACB交AB于E,
∴ ∠ACE=45°,
∵ ∠A=72°,
∴ ∠ACD=90°﹣72°=18°,
∴ ∠ECD=∠ACE﹣∠ACD=27°,
∵? EF∥CD,
∴ ∠FEC=∠ECD=27°.
【分析】(1)根据垂直的定义可得 ∠CDB=∠FEB=90°, 然后根据同位角相等两直线平行即可求解; (2)根据角平分线的定义可得 ∠ACE=45°, 再根据三角形的内角和等于180°可得 ∠ACD=18°,?进而求出 ?∠ECD=∠ACE﹣∠ACD=27°, 然后根据两直线平行内错角相等即可求解.21*cnjy*com
三、真题演练
10. C
解:如图 ∵∠BCA=60°,∠DCE=45° ∴∠2=180°-60°-45°=75° ∵FH∥BC ∴∠1=∠2=75° 故答案为:C 【分析】由已知可得∠BCA=60°,∠DCE=45°,再根据平角的定义求出∠2的度数,然后利用平行线的性质,可求出∠1的度数。21·世纪*教育网
11. B
解:如图,
∵∠2=∠3=100°,∠1=70°
∴a、b两直线所夹的锐角为:180°-∠1-∠3=180°-70°-100°=10°
故答案为:B
【分析】根据对顶角相等,可求出∠3的度数,再利用三角形内角和定理就可求出a、b两直线所夹的锐角的度数。【版权所有:21教育】
12. A
解:由题意知 , ,
∵ ,
∴ ,
在 中,
,
故答案为:A.
【分析】根据二直线平行,内错角相等得出 ,然后根据三角形的内角和,
,即可算出答案。
13. 60或10
解:∵ △ABC中,∠A=50°,∠B=30°, ∴∠ACB=180°-∠A-∠B=180°-50°-30°=100° ∵ 点D在AB边上, △ACD为直角三角形 当∠ACD=90°,∠BCD=∠ACB-∠ACD=100°-90°=10°; 当∠ADC=90°时,∠ACD=90°-∠A=90°-50°=40° ∴∠BCD=∠ACB-∠ACD=100°-40°=60°; 故答案为:60或10 【分析】利用三角形内角和定理求出∠ACB的度数,再由已知点D在AB边上, △ACD为直角三角形,分两种情况讨论:当∠ACD=90°时,当∠ADC=90°时,分别求出∠BCD的度数。21教育名师原创作品
一、基础巩固(共3题;)
1.己知钝角△ABC中,∠A=30°,则下列结论正确的是( ??)
A.?0°<∠B<60°???????????B.?90°<∠B<150°???????????C.?0°<∠B<60°或90°<∠B<150°???????????D.?以上都不对
2.适合条件∠A= =∠B= =∠C的△ABC是(? ? )
A.?锐角三角形???????????????????????B.?直角三角形???????????????????????C.?钝角三角形???????????????????????D.?等边三角形
3.将一把直尺与一块含30°和60°角的三角板ABC按如图所示的位置放置,直尺的一边恰好经过点A,如果∠CDE=50°,那么∠BAF的度数为( ??) 2-1-c-n-j-y
A.?15°???????????????????????????????????????B.?20°???????????????????????????????????????C.?30°???????????????????????????????????????D.?40°
二、强化提升(共6题;)
4.如图,直线 ,若 , ,则 的大小为(??? )
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
5.如图,公园A在公园B的北偏东50°方向,公园C在公园B的北偏西25°方向,若A,B两公园到公园C的两直线的夹角∠C为35°,那么公园C在公园A的( ??) 21*cnjy*com
A.?西北方向??????????????????B.?北偏西60°方向??????????????????C.?北偏西70°方向??????????????????D.?南偏东75°方向
6.已知三角形ABC的三个内角满足关系∠B+∠C=3∠A,则此三角形(?? ?).
A.?一定有一个内角为45°?????B.?一定有一个内角为60°?????C.?一定是直角三角形?????D.?一定是钝角三角形
7.如图,在△ABC中,OB,OC分别为∠ABC和∠ACB的平分线,且∠A=70°,则∠BOC=________.
8.如图,AB∥CD,过直线EF上的点G作GH⊥AB,若∠1=50°,则∠2=________°。
第7题图 第8题图
9.如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
(1)CD与EF平行吗?并说明理由;
(2)若∠A=72°,求∠FEC的度数.
三、真题演练(共4题;)
10.将—副三角板按如图所示的位置摆放在直尺上,则∠1的度数为(?? ?? )。
A.?60°???????????????????????????????????????B.?65°???????????????????????????????????????C.?75°???????????????????????????????????????D.?85°
11.如图,墙上钉着三根木条,a,b,c,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角是( ??) 21·cn·jy·com
A.?5°???????????????????????????????????????B.?10°???????????????????????????????????????C.?30°???????????????????????????????????????D.?70°
12.一副三角板如图摆放(直角顶点 重合),边 与 交于点 , ,则 等于(?? ? )
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
13.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为________度. 【来源:21cnj*y.co*m】
答案解析部分
一、基础巩固
1. C
解:∵∠A+∠B+∠C=180°,∠B=30° ∴∠B+∠C=150° ∵△ABC是钝角三角形 ∴ 0°<∠B<60°或90°<∠B<150° , 故答案为:C 【分析】根据三角形内角和定理,就可求出∠B+∠C的值,再根据钝角三角形的定义,就可求出∠B的度数的取值范围。21cnjy.com
2. B
解:∵∠A= ∠B= ∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180 ?,即6∠A=180 ?,
∴∠A=30 ? ,
∴∠B=60 ? ,∠C=90 ? ,
∴△ABC为直角三角形.
故答案为:B. 【分析】由已知条件可得∠B=2∠A,∠C=3∠A,再根据三角形的内角和定理可得关于∠A的方程,解方程可求得各角的度数,由角的度数即可判断三角形的形状。www-2-1-cnjy-com
3. B
解:由图可得,∠CDE=50°,∠C=90°,
∴∠CED=40°,
又∵DE∥AF,
∴∠CAF=40°,
∵∠BAC=60°,
∴∠BAF=60°﹣40°=20°,
故答案为:B.
【分析】根据三角形的内角和定理可求出∠CED的度数,根据两直线平行,同位角相等可求出∠CAF的度数,利用角的和差关系求出∠BAF的度数.www.21-cn-jy.com
二、强化提升
4. C
解:如图,
∵l1∥l2 ,
∴∠1=∠4=72°,
∵∠2+∠3+∠4=180°,
∴∠2=180°-∠3-∠4=180°-50°-72°=58°,
故答案为:C. 【分析】根据两直线平行内错角相等,可得∠1=∠4=72°,利用三角形内角和定理可求出∠2的度数.
5. B
解:如图, 由题意得BD∥EF,∠CBA=50°+25°=75°, ∴∠BAE=∠DBA=50°, 在△ABC中,∠CAB=180°-∠C-∠CBA=70°, ∴∠CAF=180°-∠CAB-∠BAE=60°, ∴ 公园C在公园A的北偏西60°方向. 21世纪教育网版权所有
故答案为:B.
【分析】根据两直线平行内错角相等,可得∠BAE=∠DBA=50°,利用三角形内角和定理求出∠CAB的度数,利用平角的定义可求出∠CAF的度数,从而可求出结论.1教育网
6. A
解:∵∠A+∠B+∠C=180°,
∴∠B+∠C=180°-∠A,
又∵∠B+∠C=3∠A,
∴3∠A=180°-∠A,
∴∠A=45°.
故答案为:A.
【分析】根据三角形的内角和定理得出∠B+∠C=180°-∠A,又 ∠B+∠C=3∠A 从而列出方程求出∠A的度数,即可得出答案。2·1·c·n·j·y
7. 125°
解:∵∠A=70°,∠A+∠ABC+∠ACB=180°
∴∠ABC+∠ACB=110°
∵OB、OC分别平分∠ABC和∠ACB
∴∠OBC= ∠ABC,∠OCB= ∠ACB,
∴∠OBC+∠OCB= (∠ABC+∠ACB)=55°
∵∠BPC+∠PBC+∠PCB=180°
∴∠BPC=125°
故答案为:125°
【分析】利用三角形内角和定理求出∠ABC+∠ACB的值,再利用角平分线的定义求出∠OBC+∠OCB的值,然后利用三角形内角和定理,在△BOC中求出∠BOC的度数。【来源:21·世纪·教育·网】
8. 40
解: ∵ ∠1=50°?,∴∠3=50°, AB∥CD,∴∠4=∠3=50°, GH⊥AB,∠GHA=90°, ∠2=90°-50°=40°。【出处:21教育名师】
【分析】由两直线平行可知同位角相等,再根据直角三角形中两锐角互余即可。
9. (1)解:∵? CD⊥AB,EF⊥AB,
∴ ∠CDB=∠FEB=90°,
∴? EF∥CD; (2)解:∵∠ ACB=90°,CE平分∠ACB交AB于E,
∴ ∠ACE=45°,
∵ ∠A=72°,
∴ ∠ACD=90°﹣72°=18°,
∴ ∠ECD=∠ACE﹣∠ACD=27°,
∵? EF∥CD,
∴ ∠FEC=∠ECD=27°.
【分析】(1)根据垂直的定义可得 ∠CDB=∠FEB=90°, 然后根据同位角相等两直线平行即可求解; (2)根据角平分线的定义可得 ∠ACE=45°, 再根据三角形的内角和等于180°可得 ∠ACD=18°,?进而求出 ?∠ECD=∠ACE﹣∠ACD=27°, 然后根据两直线平行内错角相等即可求解.21*cnjy*com
三、真题演练
10. C
解:如图 ∵∠BCA=60°,∠DCE=45° ∴∠2=180°-60°-45°=75° ∵FH∥BC ∴∠1=∠2=75° 故答案为:C 【分析】由已知可得∠BCA=60°,∠DCE=45°,再根据平角的定义求出∠2的度数,然后利用平行线的性质,可求出∠1的度数。21·世纪*教育网
11. B
解:如图,
∵∠2=∠3=100°,∠1=70°
∴a、b两直线所夹的锐角为:180°-∠1-∠3=180°-70°-100°=10°
故答案为:B
【分析】根据对顶角相等,可求出∠3的度数,再利用三角形内角和定理就可求出a、b两直线所夹的锐角的度数。【版权所有:21教育】
12. A
解:由题意知 , ,
∵ ,
∴ ,
在 中,
,
故答案为:A.
【分析】根据二直线平行,内错角相等得出 ,然后根据三角形的内角和,
,即可算出答案。
13. 60或10
解:∵ △ABC中,∠A=50°,∠B=30°, ∴∠ACB=180°-∠A-∠B=180°-50°-30°=100° ∵ 点D在AB边上, △ACD为直角三角形 当∠ACD=90°,∠BCD=∠ACB-∠ACD=100°-90°=10°; 当∠ADC=90°时,∠ACD=90°-∠A=90°-50°=40° ∴∠BCD=∠ACB-∠ACD=100°-40°=60°; 故答案为:60或10 【分析】利用三角形内角和定理求出∠ACB的度数,再由已知点D在AB边上, △ACD为直角三角形,分两种情况讨论:当∠ACD=90°时,当∠ADC=90°时,分别求出∠BCD的度数。21教育名师原创作品
