11.2.2 三角形的外角(解析版)同步练习
文档属性
| 名称 | 11.2.2 三角形的外角(解析版)同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-26 00:00:00 | ||
图片预览


文档简介
初中数学人教版八年级上学期 第十一章 11.2.2 三角形的外角
一、基础巩固(共3题;)
1.如图, , , ,求 .
2.如图,一副三角板的三个内角分别是90,45°,45°和90°,60°,30°,按如图所示叠放在一起(点A,D,B在同一直线上).若固定△ABC,将△BDE绕着公共顶点B顺时针旋转a度(0
3.已知:直线l1∥l2 , 一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于________?.
二、真题演练(共3题;)
4.“三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=75°,则∠CDE的度数是( ??) 2·1·c·n·j·y
A.?60°???????????????????????????????????????B.?65°???????????????????????????????????????C.?75°???????????????????????????????????????D.?80°
5.将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则 的度数是(?? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
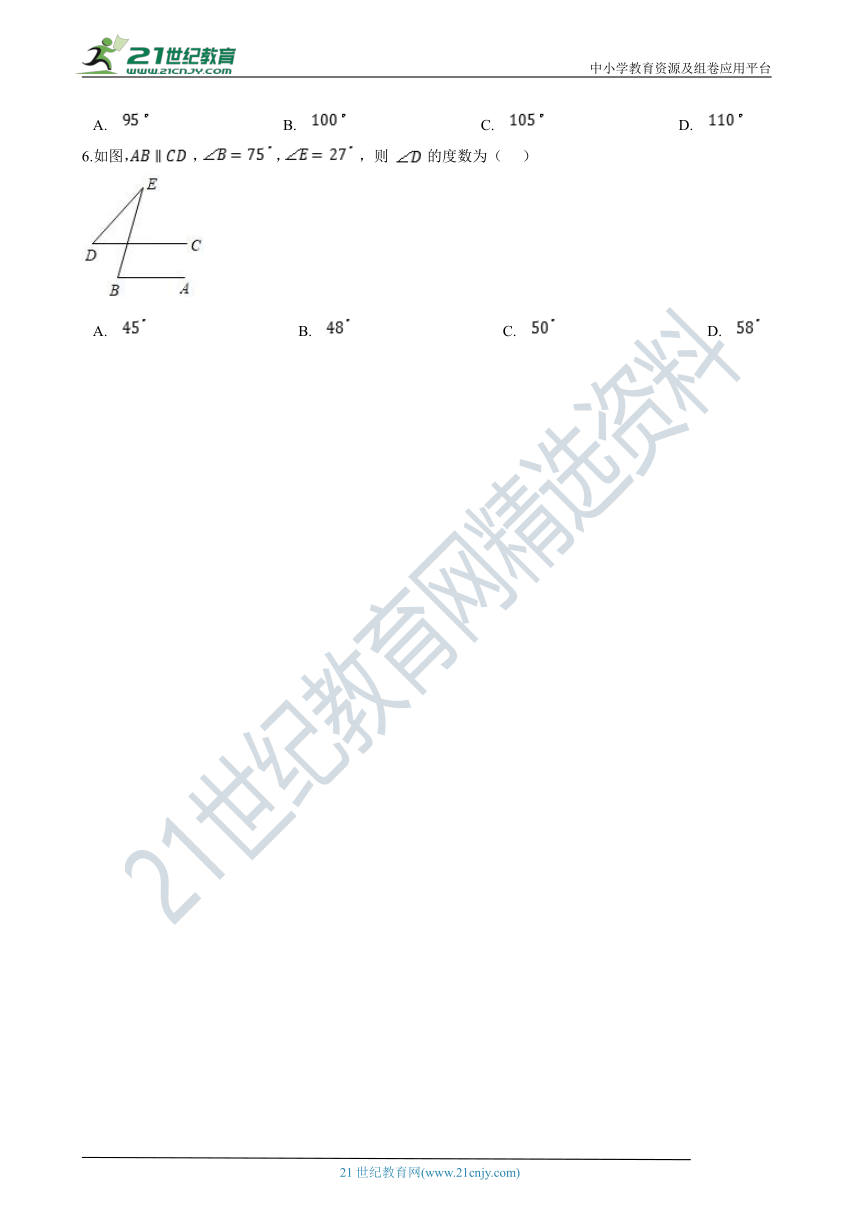
6.如图, , , ,则 的度数为(??? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
答案解析部分
一、基础巩固
1.∵AB∥CD,∠A=60°,
∴∠DOE=∠A=60°,
又∵∠C=∠E,∠DOE=∠C+∠E,
∴∠E= ∠DOE=30°
【分析】根据二直线平行,内错角相等得出 ∠DOE=∠A=60°, 然后根据三角形的一个外角等于与它不相邻的两个内角的和即可得出 ∠DOE=∠C+∠E, 又 ∠C=∠E, 从而代入即可算出答案。
2. 45°,75°,165°
解:如图,当DE∥AB即D1E1∥AB时
∵△DBE和△D1BE1是等腰直角三角形, ∴∠E1=∠DBE1=45°, ∴ 旋转角a=45°; 当DE∥CB即D2E2∥CB时,如图 ∴∠E2=∠E2BC=45° ∵∠ABC=30° ∴∠DBE2=∠ABC+∠E2BC=30°+45°=75° ∴旋转角a=75°; 当DE∥CB即D3E3∥CB时,延长AB交D3E3于点F,如图?? ∴∠A=∠BFE3=60° ∵∠BFE3=∠D3+∠D3BF ∴∠D3BF=60°-45°=15° ∴∠DBD3=180°-∠D3BF=180°-15°=165° ∴旋转角a=165°; 故答案为: 45°,75°,165° 【分析】抓住已知条件,要使边DE与△ABC的某一边平行时,因此分三种情况讨论:D1E1∥AB时,利用平行线的性质,可得出旋转角a的度数;当D2E2∥CB时,利用平行线的性质,可求出∠E2BC(旋转角a)的度数;再根据∠DBE2=∠ABC+∠E2BC,代入计算可求出∠DBE2(旋转角a)的度数;当D3E3∥CB时,利用平行线的性质,可求出∠BFE3的度数,再根据三角形外角的性质,可得到D3BF的度数,然后利用邻补角的定义即可求出∠DBD3(旋转角a)的度数;综上所述,可得出旋转角a的度数。
3. 35°
解:如图: 可得出∠3=∠A+∠1=55°, 又∵l1∥l2 , ∴∠3=∠4(同位角相等) ∠EFC=90°-55°=35°, ∴∠2=35°. 【分析】根据三角形的外角性质和同位角的性质,可得出角的度数。21cnjy.com
二、真题演练
4. D
解:∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
设∠O=∠ODC=x,
∴∠DCE=∠DEC=2x,
∴∠CDE=180°-∠DCE-∠DEC=180°-4x,
∵∠BDE=75°,
∴∠ODC+∠CDE+∠BDE=180°,
即x+180°-4x+75°=180°,
解得:x=25°,
∠CDE=180°-4x=80°.
故答案为:D.
【分析】由等腰三角形性质得∠O=∠ODC,∠DCE=∠DEC,设∠O=∠ODC=x,由三角形外角性质和三角形内角和定理得∠DCE=∠DEC=2x,∠CDE=180°-4x,根据平角性质列出方程,解之即可的求得x值,再由∠CDE=180°-4x=80°即可求得答案.21世纪教育网版权所有
5. C
解:由题意得,∠2=45°,∠4=90°-30°=60°, ∴∠3=∠2=45°, 由三角形的外角性质可知,∠1=∠3+∠4=105°。 故答案为:C 【分析】三角形的外角等于不相邻的两个内角之和。·com
6. B
解:如图,
,
,
,
。
故答案为:B。
【分析】根据二直线平行,同位角相等得出 , 根据三角形的一个外角等于与之不相邻的两个内角的和得出 , 从而即可算出答案。www.21-cn-jy.com
一、基础巩固(共3题;)
1.如图, , , ,求 .
2.如图,一副三角板的三个内角分别是90,45°,45°和90°,60°,30°,按如图所示叠放在一起(点A,D,B在同一直线上).若固定△ABC,将△BDE绕着公共顶点B顺时针旋转a度(0
3.已知:直线l1∥l2 , 一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于________?.
二、真题演练(共3题;)
4.“三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=75°,则∠CDE的度数是( ??) 2·1·c·n·j·y
A.?60°???????????????????????????????????????B.?65°???????????????????????????????????????C.?75°???????????????????????????????????????D.?80°
5.将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则 的度数是(?? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
6.如图, , , ,则 的度数为(??? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
答案解析部分
一、基础巩固
1.∵AB∥CD,∠A=60°,
∴∠DOE=∠A=60°,
又∵∠C=∠E,∠DOE=∠C+∠E,
∴∠E= ∠DOE=30°
【分析】根据二直线平行,内错角相等得出 ∠DOE=∠A=60°, 然后根据三角形的一个外角等于与它不相邻的两个内角的和即可得出 ∠DOE=∠C+∠E, 又 ∠C=∠E, 从而代入即可算出答案。
2. 45°,75°,165°
解:如图,当DE∥AB即D1E1∥AB时
∵△DBE和△D1BE1是等腰直角三角形, ∴∠E1=∠DBE1=45°, ∴ 旋转角a=45°; 当DE∥CB即D2E2∥CB时,如图 ∴∠E2=∠E2BC=45° ∵∠ABC=30° ∴∠DBE2=∠ABC+∠E2BC=30°+45°=75° ∴旋转角a=75°; 当DE∥CB即D3E3∥CB时,延长AB交D3E3于点F,如图?? ∴∠A=∠BFE3=60° ∵∠BFE3=∠D3+∠D3BF ∴∠D3BF=60°-45°=15° ∴∠DBD3=180°-∠D3BF=180°-15°=165° ∴旋转角a=165°; 故答案为: 45°,75°,165° 【分析】抓住已知条件,要使边DE与△ABC的某一边平行时,因此分三种情况讨论:D1E1∥AB时,利用平行线的性质,可得出旋转角a的度数;当D2E2∥CB时,利用平行线的性质,可求出∠E2BC(旋转角a)的度数;再根据∠DBE2=∠ABC+∠E2BC,代入计算可求出∠DBE2(旋转角a)的度数;当D3E3∥CB时,利用平行线的性质,可求出∠BFE3的度数,再根据三角形外角的性质,可得到D3BF的度数,然后利用邻补角的定义即可求出∠DBD3(旋转角a)的度数;综上所述,可得出旋转角a的度数。
3. 35°
解:如图: 可得出∠3=∠A+∠1=55°, 又∵l1∥l2 , ∴∠3=∠4(同位角相等) ∠EFC=90°-55°=35°, ∴∠2=35°. 【分析】根据三角形的外角性质和同位角的性质,可得出角的度数。21cnjy.com
二、真题演练
4. D
解:∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
设∠O=∠ODC=x,
∴∠DCE=∠DEC=2x,
∴∠CDE=180°-∠DCE-∠DEC=180°-4x,
∵∠BDE=75°,
∴∠ODC+∠CDE+∠BDE=180°,
即x+180°-4x+75°=180°,
解得:x=25°,
∠CDE=180°-4x=80°.
故答案为:D.
【分析】由等腰三角形性质得∠O=∠ODC,∠DCE=∠DEC,设∠O=∠ODC=x,由三角形外角性质和三角形内角和定理得∠DCE=∠DEC=2x,∠CDE=180°-4x,根据平角性质列出方程,解之即可的求得x值,再由∠CDE=180°-4x=80°即可求得答案.21世纪教育网版权所有
5. C
解:由题意得,∠2=45°,∠4=90°-30°=60°, ∴∠3=∠2=45°, 由三角形的外角性质可知,∠1=∠3+∠4=105°。 故答案为:C 【分析】三角形的外角等于不相邻的两个内角之和。·com
6. B
解:如图,
,
,
,
。
故答案为:B。
【分析】根据二直线平行,同位角相等得出 , 根据三角形的一个外角等于与之不相邻的两个内角的和得出 , 从而即可算出答案。www.21-cn-jy.com
