11.3.2 多边形的内角和(解析版)同步练习
文档属性
| 名称 | 11.3.2 多边形的内角和(解析版)同步练习 | 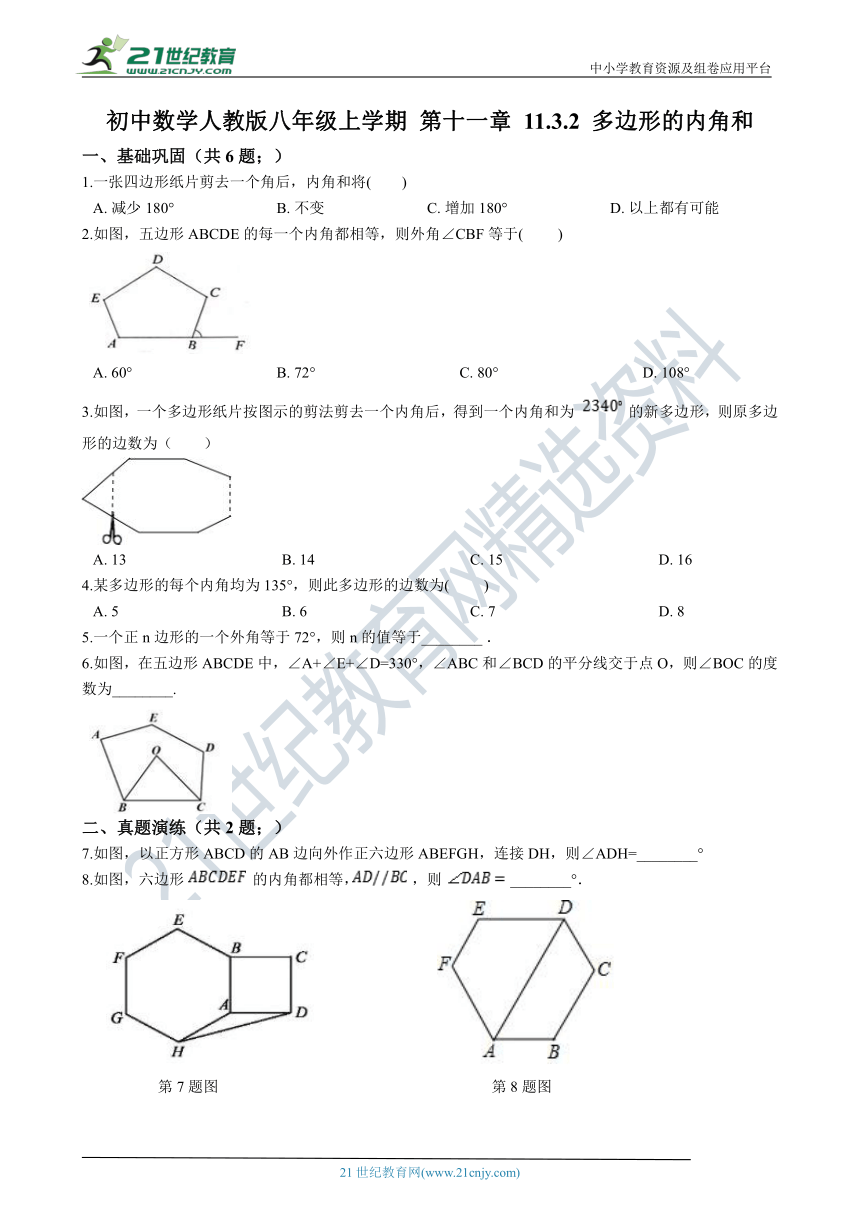 | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-26 16:58:53 | ||
图片预览


文档简介
初中数学人教版八年级上学期 第十一章 11.3.2 多边形的内角和
一、基础巩固(共6题;)
1.一张四边形纸片剪去一个角后,内角和将(?? )
A.?减少180°???????????????????????????B.?不变???????????????????????????C.?增加180°???????????????????????????D.?以上都有可能
2.如图,五边形ABCDE的每一个内角都相等,则外角∠CBF等于( ??? )
A.?60°??????????????????????????????????????B.?72°??????????????????????????????????????C.?80°??????????????????????????????????????D.?108°
3.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为 的新多边形,则原多边形的边数为(? ? ) 21·cn·jy·com
A.?13?????????????????????????????????????????B.?14?????????????????????????????????????????C.?15?????????????????????????????????????????D.?16
4.某多边形的每个内角均为135°,则此多边形的边数为(?? ? )
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
5.一个正n边形的一个外角等于72°,则n的值等于________?.
6.如图,在五边形ABCDE中,∠A+∠E+∠D=330°,∠ABC和∠BCD的平分线交于点O,则∠BOC的度数为________. 21cnjy.com
二、真题演练(共2题;)
7.如图,以正方形ABCD的AB边向外作正六边形ABEFGH,连接DH,则∠ADH=________°
8.如图,六边形 的内角都相等, ,则 ________°.
第7题图 第8题图
答案解析部分
一、基础巩固
1. C
解:∵四角纸片是一个四边形, 剪去一个角后成为一个五边形, 四边形的内角和是360°,五边形的内角和是(5-2)×180=540°, 则内角和增加540°-360°=180°. 故答案为:C 21教育网
【分析】先明确四边形剪去一个角后成为五边形,分别求四边形和五边形内角和,相减即可得出答案。
2. B
解:因为是正五边形,则每个外角=. ,故答案为: B
【分析】根据正多边形的外角和等于 计算即可求得 ∠CBF 的大小。
3. B
解:减去一个角之后,得到的多边形比原来的多边形多一条边,只要求出现在多边形的边数就可以得出原多边形的边数.2340÷180+2=15 15-1=14 【分析】由多边形的内角和=(n-2)·180°可求得多边形的边数,再根据新多边形比原多边形多一条边可求解。2·1·c·n·j·y
4. D
解:∵每个内角为135°,则每个外角等于45°, ∴n= =8 , 故答案为:D 【分析】先根据每个内角和其外角之和等于180°,求出每个外角,再根据外角和公式求出n即可。
5. 5
解:由题意得:n=?. 故答案为:5 【分析】n边形外角和是360°,则正n边形每个外角等于= , 据此求解即可。【来源:21·世纪·教育·网】
6. 75
解:∵五边形的内角和等于540°, ∠A+∠E+∠D=330° ∴∠ABC+∠BCD=540°?330°=210° ∵ ∠ABC和∠BCD的平分线交于点O ∴2(∠OBC+∠OCB)=∠ABC+∠BCD=210° ∴∠OBC+∠OCB=105° ∴∠BOC=180°?(∠OBC+∠OCB)=180°-105°=75° 故答案为:75° 【分析】利用五边形的内角和求出∠ABC+∠BCD的值,再根据角平分线的定义求出∠OBC+∠OCB,然后利用三角形内角和定理可求出∠BOC的度数,21·世纪*教育网
二、真题演练
7. 15
解:∵正六边形ABEFGH的内角为120°,
正方形ABCD的内角为90°,
∴∠DAH =360°-90°-120°=150°,
∵AB=AH,
∴∠ADH= ×(180°-150°)=15°,
故答案为:15 【分析】先求出正六边形ABEFGH的内角∠BAH和正方形ABCD的内角∠BAD,从而可求得∠DAH,然后根据等腰三角形的性质和三角形内角和定理求出∠ADH。www.21-cn-jy.com
8. 60°
解:在六边形 中 , , ,
∴ ,
∵ ,
∴ ,
故答案为:60°.
【分析】先求出多边形的内角和,然后求出各内角的度数,根据两直线平行,同旁内角互补求出∠DAB的度数.21世纪教育网版权所有
一、基础巩固(共6题;)
1.一张四边形纸片剪去一个角后,内角和将(?? )
A.?减少180°???????????????????????????B.?不变???????????????????????????C.?增加180°???????????????????????????D.?以上都有可能
2.如图,五边形ABCDE的每一个内角都相等,则外角∠CBF等于( ??? )
A.?60°??????????????????????????????????????B.?72°??????????????????????????????????????C.?80°??????????????????????????????????????D.?108°
3.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为 的新多边形,则原多边形的边数为(? ? ) 21·cn·jy·com
A.?13?????????????????????????????????????????B.?14?????????????????????????????????????????C.?15?????????????????????????????????????????D.?16
4.某多边形的每个内角均为135°,则此多边形的边数为(?? ? )
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
5.一个正n边形的一个外角等于72°,则n的值等于________?.
6.如图,在五边形ABCDE中,∠A+∠E+∠D=330°,∠ABC和∠BCD的平分线交于点O,则∠BOC的度数为________. 21cnjy.com
二、真题演练(共2题;)
7.如图,以正方形ABCD的AB边向外作正六边形ABEFGH,连接DH,则∠ADH=________°
8.如图,六边形 的内角都相等, ,则 ________°.
第7题图 第8题图
答案解析部分
一、基础巩固
1. C
解:∵四角纸片是一个四边形, 剪去一个角后成为一个五边形, 四边形的内角和是360°,五边形的内角和是(5-2)×180=540°, 则内角和增加540°-360°=180°. 故答案为:C 21教育网
【分析】先明确四边形剪去一个角后成为五边形,分别求四边形和五边形内角和,相减即可得出答案。
2. B
解:因为是正五边形,则每个外角=. ,故答案为: B
【分析】根据正多边形的外角和等于 计算即可求得 ∠CBF 的大小。
3. B
解:减去一个角之后,得到的多边形比原来的多边形多一条边,只要求出现在多边形的边数就可以得出原多边形的边数.2340÷180+2=15 15-1=14 【分析】由多边形的内角和=(n-2)·180°可求得多边形的边数,再根据新多边形比原多边形多一条边可求解。2·1·c·n·j·y
4. D
解:∵每个内角为135°,则每个外角等于45°, ∴n= =8 , 故答案为:D 【分析】先根据每个内角和其外角之和等于180°,求出每个外角,再根据外角和公式求出n即可。
5. 5
解:由题意得:n=?. 故答案为:5 【分析】n边形外角和是360°,则正n边形每个外角等于= , 据此求解即可。【来源:21·世纪·教育·网】
6. 75
解:∵五边形的内角和等于540°, ∠A+∠E+∠D=330° ∴∠ABC+∠BCD=540°?330°=210° ∵ ∠ABC和∠BCD的平分线交于点O ∴2(∠OBC+∠OCB)=∠ABC+∠BCD=210° ∴∠OBC+∠OCB=105° ∴∠BOC=180°?(∠OBC+∠OCB)=180°-105°=75° 故答案为:75° 【分析】利用五边形的内角和求出∠ABC+∠BCD的值,再根据角平分线的定义求出∠OBC+∠OCB,然后利用三角形内角和定理可求出∠BOC的度数,21·世纪*教育网
二、真题演练
7. 15
解:∵正六边形ABEFGH的内角为120°,
正方形ABCD的内角为90°,
∴∠DAH =360°-90°-120°=150°,
∵AB=AH,
∴∠ADH= ×(180°-150°)=15°,
故答案为:15 【分析】先求出正六边形ABEFGH的内角∠BAH和正方形ABCD的内角∠BAD,从而可求得∠DAH,然后根据等腰三角形的性质和三角形内角和定理求出∠ADH。www.21-cn-jy.com
8. 60°
解:在六边形 中 , , ,
∴ ,
∵ ,
∴ ,
故答案为:60°.
【分析】先求出多边形的内角和,然后求出各内角的度数,根据两直线平行,同旁内角互补求出∠DAB的度数.21世纪教育网版权所有
