21.2.3 因式分解法(解析版)同步练习
文档属性
| 名称 | 21.2.3 因式分解法(解析版)同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-26 00:00:00 | ||
图片预览


文档简介
初中数学人教版九年级上学期 第二十一章 21.2.3 因式分解法
一、基础巩固(共6题;)
1.一个三角形的两边长分别为3和6,第三边长是方程x2﹣10x+21=0的解,则三角形的周长为( ??)
A.?12???????????????????????????????????B.?16???????????????????????????????????C.?12或16???????????????????????????????????D.?不能确定
2.解方程:x2﹣3|x﹣1|﹣1=0
3.解方程:
(1)(x+2)2=3(x+2) (2)2x2+6x+3=0
4.阅读与思考:整式乘法与因式分解是方向相反的变形由(x+p)(x+q)=x2+(P+q)+pq得
X2+(p+q)x+Pq=(x+P)(x+q)利用这个式子可以将某些二次项系数是1的二次三项式分解因式,
例如:将式子x2+3+2分解因式。分析:这个式子的常数项2=1×2,一次项系数3=1+2所以
X2+3x+2=x2+(1+2)x+1×2,x2+3x+2=(x+1)(x+2)
请仿照上面的方法,解答下列问题
(1)分解因式:x2+6x-27
(2)若x2+px+8可分解为两个一次因式的积,则整数p的所有可能值是________
(3)利用因式分解法解方程:x2-4x-12=0
5.已知:关于x的一元二次方程x2-3x-k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请选择一个k的负整数值,并求出方程的根.
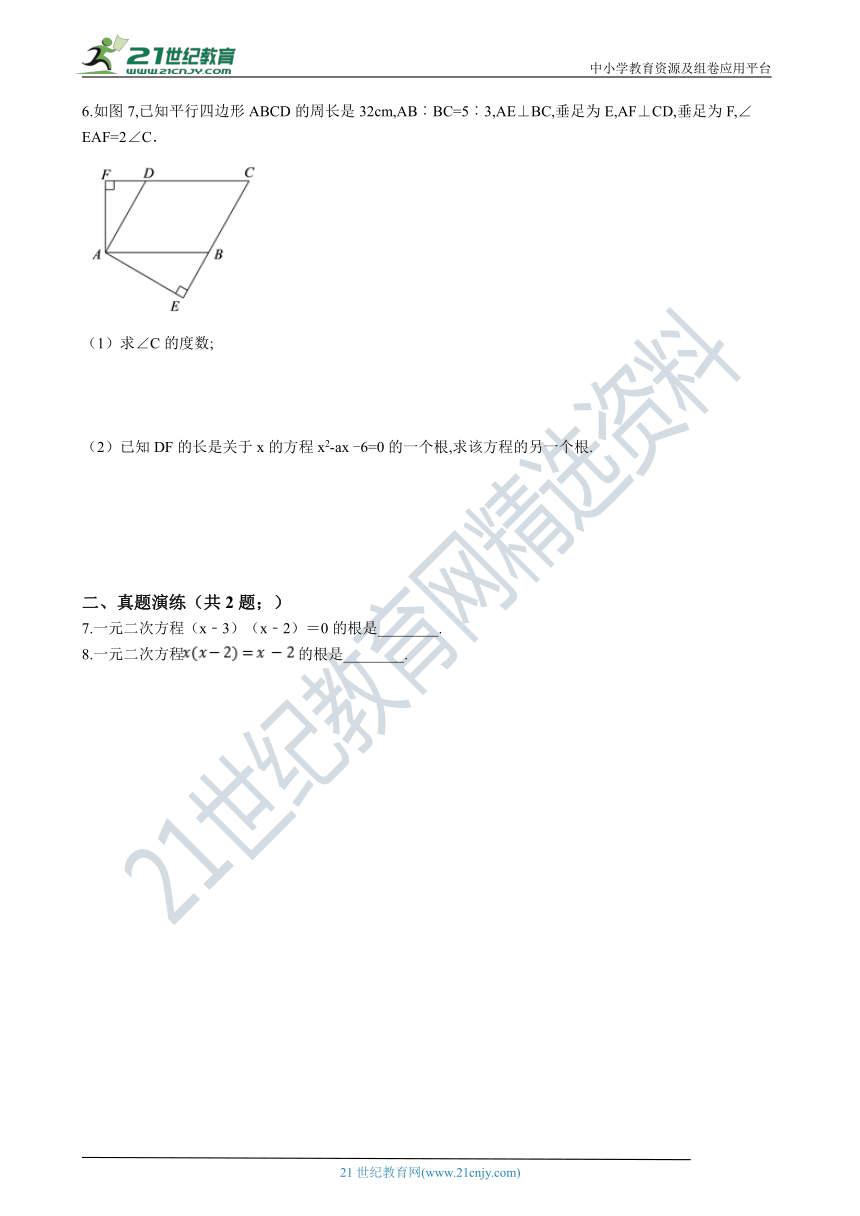
6.如图7,已知平行四边形ABCD的周长是32cm,AB︰BC=5︰3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C. 21教育网
(1)求∠C的度数;
(2)已知DF的长是关于x的方程x2-ax -6=0的一个根,求该方程的另一个根.
二、真题演练(共2题;)
7.一元二次方程(x﹣3)(x﹣2)=0的根是________.
8.一元二次方程 的根是________.
答案解析部分
一、基础巩固
1. B
解:x2﹣10x+21=0,
(x﹣3)(x﹣7)=0,
x﹣3=0或x﹣7=0,
所以x1=3,x2=7,
而3+3=6,
所以三角形的第三边为7,
所以这个三角形的周长为3+6+7=16。
故答案为:B。
【分析】先用因式分解法求出方程 x2﹣10x+21=0的解 ,然后根据三角形的三边关系判断出三角形的第三边,进而根据三角形周长的计算方法算出答案即可。21cnjy.com
2. 解:①当x﹣1≥0时|x﹣1|=x﹣1,
得方程,x2﹣3|x﹣1|﹣1=0,
去掉绝对值得,x2﹣3x+2=0
因式分解得(x﹣1)(x﹣2)=0
解得x1=1,x2=2;
②当x﹣1<0时|x﹣1|=﹣x+1,
得方程x2﹣3|x﹣1|﹣1=0
去掉绝对值得x2+3x﹣4=0
因式分解得,(x﹣1)(x+4)=0
解得x1=1(舍去),x2=﹣4.
∴原方程的根是x1=1,x2=2,x3=﹣4
解:含绝对值的方程,分 ①当x﹣1≥0 , ②当x﹣1<0时 两种情况分别去掉绝对值符号,得出方程,求解并检验即可得出原方程的解。21·cn·jy·com
3. (1)解:(x+2)2-3(x+2)=0
(x+2)(x+2-3)=0
∴(x+2)(x-1)=0
∴x+2=0或x-1=0
∴x1=-2,x2=1 (2)解:∵a=2.b=6.c=3
∴b2-4ac=62-4×2×3=12
∴x=
∴x1= ,x2=
解:(1)观察方程的特点:方程两边含有公因式(x+2),因此移项后,利用因式分解法解方程。 (2)观察方程的特点,左边不能分解因式,因此利用公式法求解,先算出 b2-4ac的值,再代入求根公式进行计算。www.21-cn-jy.com
4. (1)解:x2+6x-27=(x+9)(x-3) (2)±9,±6 (3)解:∵方程分解得:(x-6)(x+2)=0 2·1·c·n·j·y
可得x-6=0或x+2=0
解得:x=6或x=-2
解:(2)∵8=1×8;8=-8×(-1);8=-2×(-4);8=-4×(-2) 【来源:21·世纪·教育·网】
则p的可能值为
-1+(-8)=-9;8+1=9;-2+(-4)=-6;
4+2=6
∴整数p的所有可能值是±9,±6
故答案为:±9,±6;
【分析】(1)题中所给的方法其实质就是十字相乘法,二次三项式中,二次项的系数是1,故只需要将常数项分解为两个因数的积,且这两个因数的和为一次项的系数,从而即可将多项成写成两个一次项的乘积形式; (2)根据题干提供的方法,找出常数项所有分解为两个因数积的方法,然后求出每一种方法中的两个因数的和即可得出P的值; (3)利用十字相乘法将方程的左边分解因式,然后根据两个因式的积为0,则这两个因式至少有一个为0,将方程降次为两个一元一次方程,解两个方程即可求出原方程的解。21·世纪*教育网
5. (1)解:∵一元二次方程x2-3x-k=0有两个不相等的实数根,
∴△=(-3)2-4×1×(-k)>0,
解得k>- . (2)解:当k=-2时,方程为x2-3x+2=0,
因式分解得(x-1)(x-2)=0,
解得x1=1,x2=2
解:(1)根据题意,一元二次方程有两个不相等的实数根,可知 △ >0,解出k值即可。 (2)将k的值代入一元二次方程,可解出x的两个值。21世纪教育网版权所有
6.(1)解:∵AE⊥BC,AF⊥CD, ∴∠E=∠F=90°, ∵四边形AECF的内角和为360°, ∴∠EAF+∠C=360°-2×90°=180°, ∵∠EAF=2∠C, ∴2∠C+∠C=180°, ∴∠C=60 (2)解:∵ABCD为平行四边形, ∴∠DAB=∠C=60°,CD∥AB, 由已知AF⊥CD,得AF⊥AB, ∴∠FAB=90°, ∴∠FAD=∠FAB-∠DAB=30°, 由平行四边形的性质,知AB=CD,AD=BC, 由周长为32cm,得AB+BC=16cm, 由AB︰BC=5︰3,可求得BC=6cm,∴AD=BC=6cm, 在Rt△ADF中,∵∠FAD=30°, ∴DF= AD=3cm, 把DF的长代入方程中,求得a=1, ∴原方程为 x2-x-6=0, 解该方程得x1=3,x2=-2, ∴方程的另一个根为x=-2 www-2-1-cnjy-com
解:(1)根据垂直的定义可求出∠E和∠F的度数,再根据四边形的内角和定理求出∠EAF+∠C=180°,然后根据∠EAF=2∠C,求出∠C的度数。 (2)利用平行四边形的性质及垂直的定义求出∠FAD,再根据平行四边形的周长及AB︰BC=5︰3,求出BC、AD,利用直角三角形的性质求出DF的长,然后将DF的值代入方程求出a的值,将a的值代入方程,就可求出方程的另一个根。2-1-c-n-j-y
二、真题演练
7. x1=3,x2=2
解:x﹣3=0或x﹣2=0, 所以x1=3,x2=2。故答案为:x1=3,x2=2。
【分析】根据两个因式的乘积为0,则这两个因式中至少有一个为0,从而将方程降次为两个一元一次方程,解两个一元一次方程即可求出原方程的解。21*cnjy*com
8. x1=1,x2=2
解: , 移项得 , ∴(x-2)(x-1)=0, ∴x-2=0,或x-1=0, 解得: x1=1,x2=2。 故答案为: x1=1,x2=2。 【分析】将方程的右边整体移到方程的左边,然后利用提公因式法将方程的左边分解因式,根据两个因式的乘积等于0,则这两个因式至少有一个为0,从而将方程降次为两个一元一次方程,解一元一次方程即可求出原方程的解。【来源:21cnj*y.co*m】
一、基础巩固(共6题;)
1.一个三角形的两边长分别为3和6,第三边长是方程x2﹣10x+21=0的解,则三角形的周长为( ??)
A.?12???????????????????????????????????B.?16???????????????????????????????????C.?12或16???????????????????????????????????D.?不能确定
2.解方程:x2﹣3|x﹣1|﹣1=0
3.解方程:
(1)(x+2)2=3(x+2) (2)2x2+6x+3=0
4.阅读与思考:整式乘法与因式分解是方向相反的变形由(x+p)(x+q)=x2+(P+q)+pq得
X2+(p+q)x+Pq=(x+P)(x+q)利用这个式子可以将某些二次项系数是1的二次三项式分解因式,
例如:将式子x2+3+2分解因式。分析:这个式子的常数项2=1×2,一次项系数3=1+2所以
X2+3x+2=x2+(1+2)x+1×2,x2+3x+2=(x+1)(x+2)
请仿照上面的方法,解答下列问题
(1)分解因式:x2+6x-27
(2)若x2+px+8可分解为两个一次因式的积,则整数p的所有可能值是________
(3)利用因式分解法解方程:x2-4x-12=0
5.已知:关于x的一元二次方程x2-3x-k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请选择一个k的负整数值,并求出方程的根.
6.如图7,已知平行四边形ABCD的周长是32cm,AB︰BC=5︰3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C. 21教育网
(1)求∠C的度数;
(2)已知DF的长是关于x的方程x2-ax -6=0的一个根,求该方程的另一个根.
二、真题演练(共2题;)
7.一元二次方程(x﹣3)(x﹣2)=0的根是________.
8.一元二次方程 的根是________.
答案解析部分
一、基础巩固
1. B
解:x2﹣10x+21=0,
(x﹣3)(x﹣7)=0,
x﹣3=0或x﹣7=0,
所以x1=3,x2=7,
而3+3=6,
所以三角形的第三边为7,
所以这个三角形的周长为3+6+7=16。
故答案为:B。
【分析】先用因式分解法求出方程 x2﹣10x+21=0的解 ,然后根据三角形的三边关系判断出三角形的第三边,进而根据三角形周长的计算方法算出答案即可。21cnjy.com
2. 解:①当x﹣1≥0时|x﹣1|=x﹣1,
得方程,x2﹣3|x﹣1|﹣1=0,
去掉绝对值得,x2﹣3x+2=0
因式分解得(x﹣1)(x﹣2)=0
解得x1=1,x2=2;
②当x﹣1<0时|x﹣1|=﹣x+1,
得方程x2﹣3|x﹣1|﹣1=0
去掉绝对值得x2+3x﹣4=0
因式分解得,(x﹣1)(x+4)=0
解得x1=1(舍去),x2=﹣4.
∴原方程的根是x1=1,x2=2,x3=﹣4
解:含绝对值的方程,分 ①当x﹣1≥0 , ②当x﹣1<0时 两种情况分别去掉绝对值符号,得出方程,求解并检验即可得出原方程的解。21·cn·jy·com
3. (1)解:(x+2)2-3(x+2)=0
(x+2)(x+2-3)=0
∴(x+2)(x-1)=0
∴x+2=0或x-1=0
∴x1=-2,x2=1 (2)解:∵a=2.b=6.c=3
∴b2-4ac=62-4×2×3=12
∴x=
∴x1= ,x2=
解:(1)观察方程的特点:方程两边含有公因式(x+2),因此移项后,利用因式分解法解方程。 (2)观察方程的特点,左边不能分解因式,因此利用公式法求解,先算出 b2-4ac的值,再代入求根公式进行计算。www.21-cn-jy.com
4. (1)解:x2+6x-27=(x+9)(x-3) (2)±9,±6 (3)解:∵方程分解得:(x-6)(x+2)=0 2·1·c·n·j·y
可得x-6=0或x+2=0
解得:x=6或x=-2
解:(2)∵8=1×8;8=-8×(-1);8=-2×(-4);8=-4×(-2) 【来源:21·世纪·教育·网】
则p的可能值为
-1+(-8)=-9;8+1=9;-2+(-4)=-6;
4+2=6
∴整数p的所有可能值是±9,±6
故答案为:±9,±6;
【分析】(1)题中所给的方法其实质就是十字相乘法,二次三项式中,二次项的系数是1,故只需要将常数项分解为两个因数的积,且这两个因数的和为一次项的系数,从而即可将多项成写成两个一次项的乘积形式; (2)根据题干提供的方法,找出常数项所有分解为两个因数积的方法,然后求出每一种方法中的两个因数的和即可得出P的值; (3)利用十字相乘法将方程的左边分解因式,然后根据两个因式的积为0,则这两个因式至少有一个为0,将方程降次为两个一元一次方程,解两个方程即可求出原方程的解。21·世纪*教育网
5. (1)解:∵一元二次方程x2-3x-k=0有两个不相等的实数根,
∴△=(-3)2-4×1×(-k)>0,
解得k>- . (2)解:当k=-2时,方程为x2-3x+2=0,
因式分解得(x-1)(x-2)=0,
解得x1=1,x2=2
解:(1)根据题意,一元二次方程有两个不相等的实数根,可知 △ >0,解出k值即可。 (2)将k的值代入一元二次方程,可解出x的两个值。21世纪教育网版权所有
6.(1)解:∵AE⊥BC,AF⊥CD, ∴∠E=∠F=90°, ∵四边形AECF的内角和为360°, ∴∠EAF+∠C=360°-2×90°=180°, ∵∠EAF=2∠C, ∴2∠C+∠C=180°, ∴∠C=60 (2)解:∵ABCD为平行四边形, ∴∠DAB=∠C=60°,CD∥AB, 由已知AF⊥CD,得AF⊥AB, ∴∠FAB=90°, ∴∠FAD=∠FAB-∠DAB=30°, 由平行四边形的性质,知AB=CD,AD=BC, 由周长为32cm,得AB+BC=16cm, 由AB︰BC=5︰3,可求得BC=6cm,∴AD=BC=6cm, 在Rt△ADF中,∵∠FAD=30°, ∴DF= AD=3cm, 把DF的长代入方程中,求得a=1, ∴原方程为 x2-x-6=0, 解该方程得x1=3,x2=-2, ∴方程的另一个根为x=-2 www-2-1-cnjy-com
解:(1)根据垂直的定义可求出∠E和∠F的度数,再根据四边形的内角和定理求出∠EAF+∠C=180°,然后根据∠EAF=2∠C,求出∠C的度数。 (2)利用平行四边形的性质及垂直的定义求出∠FAD,再根据平行四边形的周长及AB︰BC=5︰3,求出BC、AD,利用直角三角形的性质求出DF的长,然后将DF的值代入方程求出a的值,将a的值代入方程,就可求出方程的另一个根。2-1-c-n-j-y
二、真题演练
7. x1=3,x2=2
解:x﹣3=0或x﹣2=0, 所以x1=3,x2=2。故答案为:x1=3,x2=2。
【分析】根据两个因式的乘积为0,则这两个因式中至少有一个为0,从而将方程降次为两个一元一次方程,解两个一元一次方程即可求出原方程的解。21*cnjy*com
8. x1=1,x2=2
解: , 移项得 , ∴(x-2)(x-1)=0, ∴x-2=0,或x-1=0, 解得: x1=1,x2=2。 故答案为: x1=1,x2=2。 【分析】将方程的右边整体移到方程的左边,然后利用提公因式法将方程的左边分解因式,根据两个因式的乘积等于0,则这两个因式至少有一个为0,从而将方程降次为两个一元一次方程,解一元一次方程即可求出原方程的解。【来源:21cnj*y.co*m】
同课章节目录
