第二章 立体几何 单元测试卷(含答案)
文档属性
| 名称 | 第二章 立体几何 单元测试卷(含答案) |

|
|
| 格式 | rar | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-28 00:00:00 | ||
图片预览




文档简介
立体几何单元测试卷
一、单选题
1.设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
A.若,,则
B.若,则
C.若,则
D.若,则
2.如图,在四面体中,若直线和相交,则它们的交点一定( )
A.在直线上 B.在直线上
C.在直线上 D.都不对
3.在矩形ABCD中,若AB=3,BC=4,PA⊥平面AC,且PA=1,则点P到对角线BD的距离为( )
A. B.
C. D.
4.四面体中,棱两两互相垂直,则顶点在底面上的正投影为的( )
A.垂心 B.重心 C.外心 D.内心
5.如图,长方体ABCD—A1B1C1D1中,∠DAD1=,∠CDC1=,那么异面直线AD1与DC1所成角的余弦值是 ( )
A. B. C. D.
6.在三棱锥中,平面,已知,则二面角的平面角是( )
A. B. C. D.
7.如图,在三棱柱ABC-A′B′C′中,点E、F、H、K分别为AC′、CB′、A′B、B′C′的中点,G为△ABC的重心,从K、H、G、B′中取一点作为P,使得该三棱柱恰有2条棱与平面PEF平行,则点P为 ( )
A.K B.H C.G D.B′
8.如图,α⊥β,α∩β=l,A∈α,B∈β,A、B到l的距离分别是a和b,AB与α、β所成的角分别是θ和φ,AB在α、β内的射影长分别是m和n,若a>b,则 ( )
A.θ>φ,m>n B.θ>φ,m<n
C.θ<φ,m<n D.θ<φ,m>n
9.点P在正方体侧面BCC1B1及其边界上运动,并且保持AP⊥BD1,则点P的轨迹为 ( )
A.线段B1C
B.BB1的中点与CC1的中点连成的线段
C.线段BC1
D.BC的中点与B1C1的中点连成的线段
10.设是异面直线,则以下四个命题:①存在分别经过直线和的两个互相垂直的平面;②存在分别经过直线和的两个平行平面;③经过直线有且只有一个平面垂直于直线;④经过直线有且只有一个平面平行于直线,其中正确的个数有( )
A. B. C. D.
二、填空题
11.如图所示,在直三棱柱 中,底面是 为直角的等腰直角三角形, 是 的中点,点 在线段 上,当 ________时, 平面 .
12.如图,在四面体A-BCD中,已知棱AC的长为 ,其余各棱长都为1,则二面角A-CD-B的平面角的余弦值为________.
13.已知四棱锥P?ABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
14.如图所示,在正方体中,分别是棱和上的点,若是直角,则________.
在正四面体中,分别是和的中点,则异面直线和所成角为__________.
平行六面体ABCD-A1B1C1D1中,已知底面四边形ABCD为矩形,∠A1AB=∠A1AD=。其中|AB|=a,|AD|=b,|AA1|=c,体对角线|A1C|=1,则c的最大值为__
17.如图,正方体的棱长为,点为的中点,在对角面上取一点,使最小,其最小值为_____
三、解答题
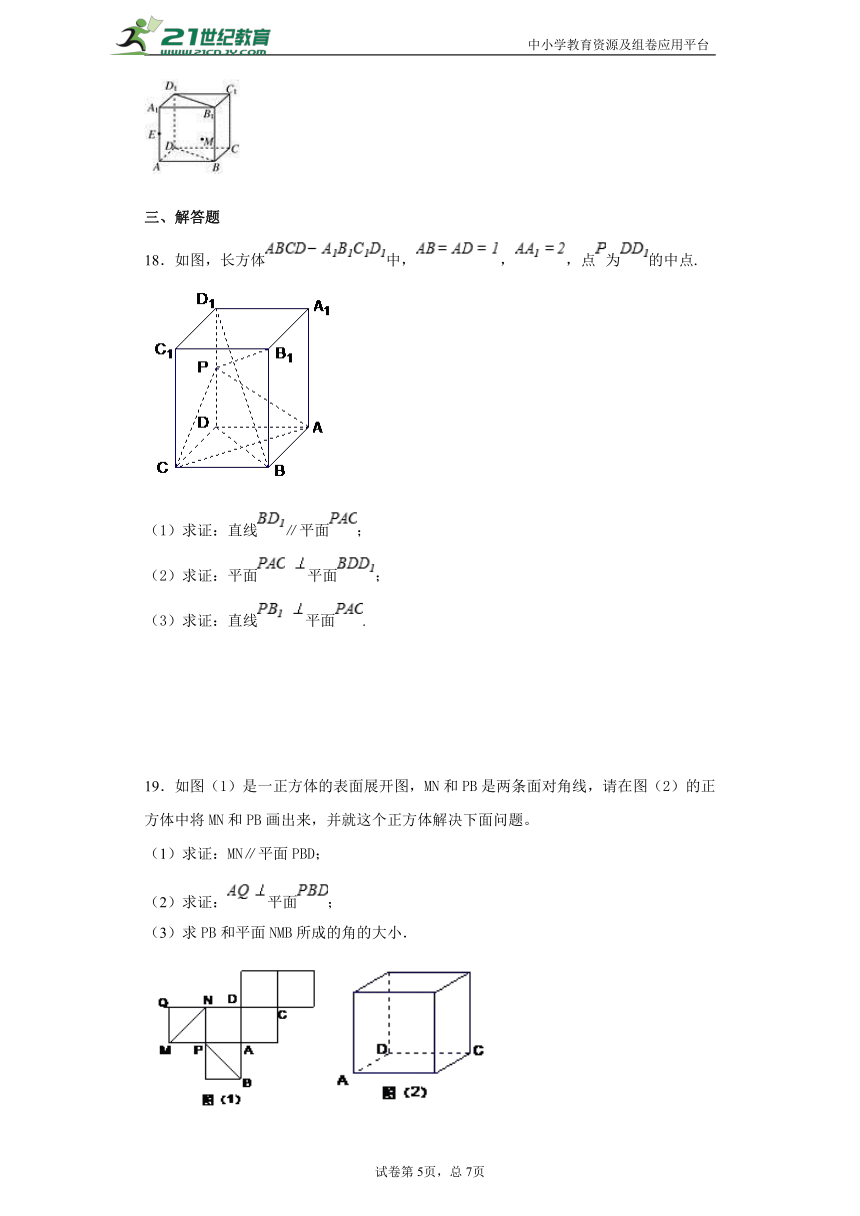
18.如图,长方体中,,,点为的中点.
(1)求证:直线∥平面;
(2)求证:平面 平面;
(3)求证:直线 平面.
19.如图(1)是一正方体的表面展开图,MN和PB是两条面对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题。
(1)求证:MN∥平面PBD;
(2)求证:平面;
(3)求PB和平面NMB所成的角的大小.
20.如图,在底面为直角梯形的四棱锥中,, 平面,,.
(1)求证: 平面;
(2)求二面角的大小.
21.四棱锥P-ABCD的底面ABCD是正方形,E,F分别为AC和PB上的点,它的直观图,正视图,侧视图如图所示.
(1)求EF与平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小.
22.如图,四棱锥中,是正三角形,四边形是矩形,且平面平面,,.
(Ⅰ)若点是的中点,求证:平面;
(Ⅱ)若点在线段上,且,当三棱锥的体积为时,求实数的值.
参考答案
1.D
【解析】
对于A,,时,若 ,则,但题目中无条件 ,故A也不一定成立;
对于B,,.显然不成立;
对于C,由面面平行的判定,一个面经过另一个面的垂线,仅有 不能得到 或,故不正确.
对于D, ,则,又,则,结论成立;
故选D
2.A
【解析】依题意有:由于交点在上,故在平面上,同理由于交点在上,故在平面上,故交点在这两个平面的交线上.
3.B
【解析】
如图, ,
则, ,
所以,故选B。
4.A
【解析】
连接,平面,因为平面,,又平面平面,,平面,得到为边上的高,同理可得为边上的高,因此为直角三角形的垂心,故选A.
5.C
【详解】
由长方体∠DAD1=,∠CDC1=,设,.连接。
由,所以异面直线AD1与DC1所成角,即。
在中,由余弦定理可得,
所以异面直线AD1与DC1所成角的余弦值是,选C.
6.D
【解析】因为平面平面,即为二面角的平面角,又,所以,故为直角三角形,,二面角的平面角是,故选D.
7.C
【解析】应用验证法:选G点为P时,EF∥A′B′且EF∥AB,此时恰有A′B′和AB平行于平面PEF,故选C.
8.D
【解析】由勾股定理得a2+n2=b2+m2=AB2.又a>b,∴m>n.
由已知得sinθ=,sinφ=,而a>b,∴sinθ<sinφ,
又θ,φ∈(0, ),∴θ<φ. 故选D.
9.A
【解析】∵AP⊥BD1恒成立,
∴要保证AP所在的平面始终垂直于BD1.
∵AC⊥BD1,AB1⊥BD1,AC∩AB1=A,
∴BD1⊥面AB1C,∴P点在线段B1C上运动.故选A.
10.C
【解析】对于①,可以在两个互相垂直的平面中,分别画一条直线,当这两条直线异面时,可判断①正确;对于②,可在两个平行平面中,分别画一条直线,当这两条直线异面时,可判断②正确;对于③,当这两条直线不垂直时,不存在这样的平面满足题意,可判断③锗误;对于④,假设过直线有两个平面与直线平行,则面相交于直线,过直线做一平面与面相交于两条直线都与直线平行,可得与平行,所以假设不成立,所以④正确,故选C.
11.或
【解析】由已知得平面,又平面,∴,故若平面,则必有,设(),则, ,又,∴,解得或,故答案为或.
12.
【解析】
如图,取中点, 中点,连接,
由题可知, 边长均为1,则,
中, ,则,得,
所以二面角的平面角即,
在中, ,
则,
所以。
13.①③
【解析】
由条件可得AB⊥平面PAD,
∴AB⊥PD,故①正确;
若平面PBC⊥平面ABCD,由PB⊥BC,
得PB⊥平面ABCD,从而PA∥PB,这是不可能的,故②错;S△PCD=CD·PD,S△PAB=AB·PA,
由AB=CD,PD>PA知③正确;
由E、F分别是棱PC、PD的中点,
可得EF∥CD,又AB∥CD,
∴EF∥AB,故AE与BF共面,④错.
14.90°
【解析】
因为正方体ABCD-A1B1C1D1中,M、N分别是棱AA1和AB上的点,若∠B1MN是直角,
所以MN⊥MB1,因为B1C1是棱,所以MN⊥B1C1,所以MN⊥平面MB1C1,
所以∠C1MN=90°
故答案为90°
15.
【解析】因为 是正四面体,所以.取 中点 ,连接 则的大小为异面直线和所成角的大小.因为,且 .所以可知.
16.
【详解】
如图,由∠A1AB=∠A1AD=可知,点在底面的射影点在直线AC上,记直线与底面所成的角为,则,
所以,所以,在中,由正弦定理可知:,所以,当时,最大为。
17.
【详解】
取中点,连接
则
(当且仅当三点共线时取等号)
又
的最小值为:
本题正确结果:
18.【详解】
(1)设AC和BD交于点O,连PO,由P,O分别是,
BD的中点,故PO//,所以直线∥平面
(2)长方体中,,底面ABCD是正方形,则ACBD
又 面ABCD,则 AC, BD∩=D
所以AC面,AC面,则平面 平面
(3)PC2=2,PB12=3,B1C2=5,所以△PB1C是直角三角形。 PC,
同理 PA,PC∩PA=P 所以直线 平面。
19.【详解】
MN和PB的位置如右图示:
(1)∵ND∥MB 且ND=MB,∴四边形NDBM为平行四边形
∴MN//DB
∵平面PDB,平面PDB
∴MN∥平面PBD
(2)∵平面ABCD,平面,∴
又∵ ∴平面,
面 ∴,同理可得,∵
∴面PDB
(3)连结PQ交MN于点E,
∵ ,
∴平面
连结BE,则为PB和平面NMB所成的角
在直角三角形PEB中∵ ∴=30°.
即PB和平面NMB所成的角为30°
20.(1)证明见解析;(2).
【解析】试题分析:(1)连接交于,由平面,可得,,可得,,,即,从而根据线面垂直的判定定理可得平面;(2) 连接,平面.,.为二面角的平面角,根据直角三角形的性质可得,进而可得二面角的大小.
试题解析:(1)连接交于,平面,平面..
又,.
,,,即.
又.平面.
(2)连接.平面.,.为二面角的平面角.
在中,,,,二面角的大小为.
21.(1)45°;(2)45°
试题解析:
根据三视图可知:PA垂直于平面ABCD,点E,F分别为AC和PB的中点,ABCD是边长为4的正方形,且PA=4.
(1)如图,取AB中点G,连接FG,GE,则FG∥PA,GE∥BC,所以FG⊥平面ABCD,∠FEG为EF与平面ABCD所成的角,在Rt△FGE中,FG=2,GE=2,所以∠FEG=45°.
(2)因为PA⊥平面ABCD,所以PA⊥BA,PA⊥CA,
所以∠BAC为二面角B-PA-C的平面角.
又因为∠BAC=45°,
所以二面角B-AP-C的平面角的大小为45°.
22.
【解析】
试题分析:(Ⅰ)连接,设,又点是的中点,由三角形中位线的性质可得//,从而由线面平行的判定理得平面;
(Ⅱ)依据题意可得:,取中点,所以,且,作于上一点,则平面,因为,可由求出,最近由求出实数的值.
试题解析(Ⅰ)如图(1),连接,设,又点是的中点,则在中,中位线//,又平面,平面。所以平面 6分
(Ⅱ)依据题意可得:,取中点,所以,且
又平面平面,则平面;(如图2)
作于上一点,则平面,
因为四边形是矩形,所以平面,则为直角三角形,
所以,则直角三角形的面积为
.
由得: 13分
试卷第1页,总3页
试卷第1页,总3页
