组内课《圆的周长》PPT课件.ppt(共25张PPT)
文档属性
| 名称 | 组内课《圆的周长》PPT课件.ppt(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 625.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-27 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
圆
的
周
长
思考:什么是平面图形周长?
围成一个平面图形所有边长的总和叫做这个图形的周长。
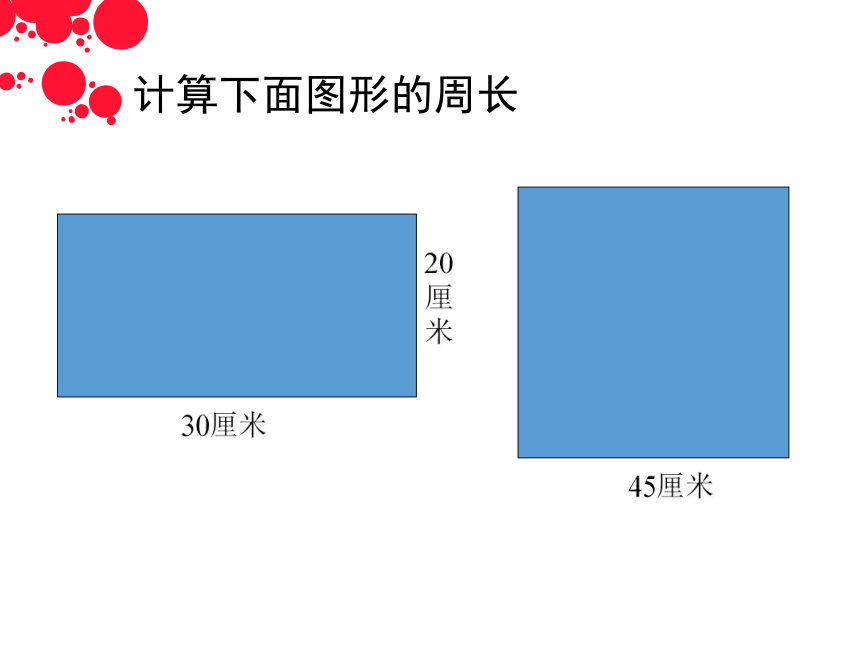
计算下面图形的周长
30厘米
45厘米
20
厘
米
想一想:什么叫圆的周长?
围成圆的曲线的长叫做圆的周长。
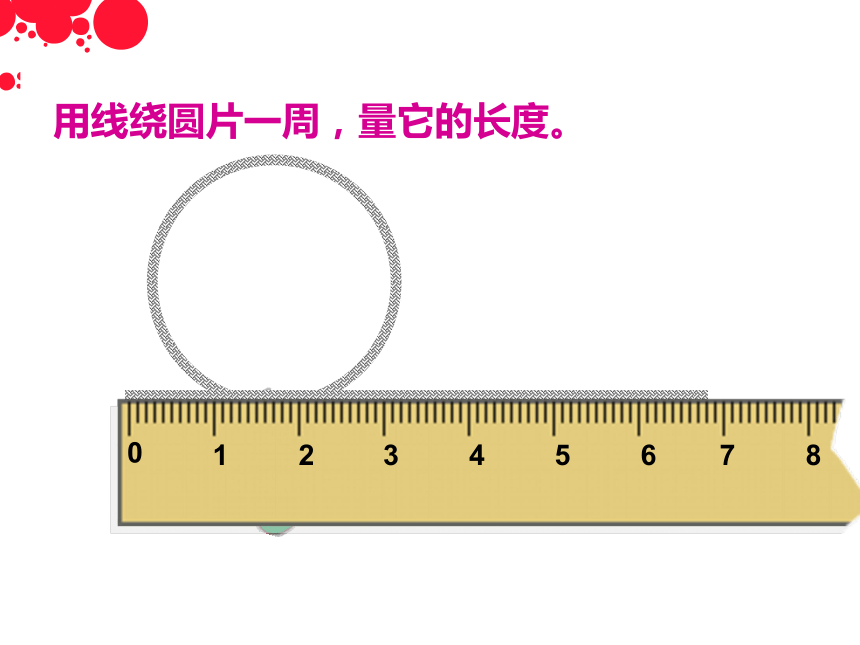
用线绕圆片一周,量它的长度。
0
1
2
3
4
6
7
8
5
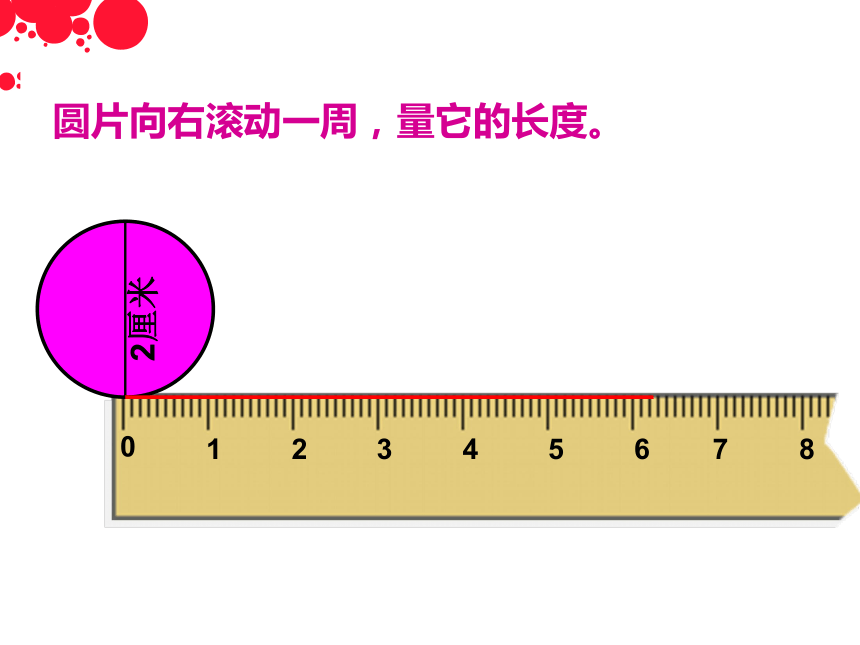
圆片向右滚动一周,量它的长度。
0
1
2
3
4
6
7
8
5
2厘米
刚才我们用什么办法“化曲为 直”测量呢 ?
一、绕线法
二、滚动法
思考:圆的周长与什么有关系?
让我们来做一个实验,找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填入下表中。看看你有什么发现。
物品名称 周长
(厘米) 直径
(厘米)
(保留两位小数)
直径
直径
直径
直径
直径
直径
直径
直径
直径
是直径的3倍多一些
圆的周长除以直径的商叫做圆周率.用字母π表示
ππ
ππ
ππ
π≈ 3.14
π是个固定的数,
也是个无限不循环小数。
大约2000多年前 我国古代的数学著作《周髀(bì)算经》中就有“周三径一”的记载,意思是说圆的周长大约是直径的3倍
大约1700年前 我国的数学家刘徽(huī)用“割圆术”来求圆周长的近似值。他从圆的内接正六边形算起,逐渐把边数加倍,正十二边形、正二十四边形····· 计算得出圆周率是3.14。并指出,内接正多边形的边数越多,周长越接近圆的周长。直到1200年后,西方人才找到类似的方法。
大约1500年前 我国的数学家祖冲之,计算出圆周率大约在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到6位小数的人。至少要比国外科学家得出这样精确的数值早1000年。
圆的周长总是直径的π倍.
圆周长÷直径= π
圆周长= π × 直径
C = π d
C = 2 π r
1.两个圆的周长相等,那么这两个圆的直径也相等。 ( )
√
2.π=3.14 ( )
×
二、选择填空。
1.车轮滚动一周,前进的距离是求车轮的( )
A.半径 B.直径 C.周长
2.圆的周长是直径的( )倍。
A.3.14 B.π C.3
3.大圆的周长除以直径的商( )小圆的周长 除以直径的商。
A.大于 B.小于 C.等于
C
B
C
一、判断。
5、圆周率与直径的关系是( )。
A、圆周率与直径的长短无关。
B、直径越长,圆周率也就越大。
C、直径越短,圆周率也就越小。
4、在下列各式中,正确的是( )。
A、π>3.14 B、π<3.14 π=3.14
A
A
求下面各圆的周长。
d=4厘米
r=1.5米
3.14×4=12.56(厘米)
3.14×1.5×2=9.42(米)
半径/cm 直径/cm 圆的周长/cm
10
5
24
10
314
6.28
一辆自行车车轮的直径是0.6米。车轮滚动一周,自行车前进多少米?
3.14×0.6=1.884(m)
答:车轮滚动一周,自行车前进1.884m.
摩天轮的半径是5米,坐着它转动一周,大约在空中转过多少米?
3.14×5×2=31.4(米)
答:大约在空中转过31.4米。
一张圆桌面的直径是0.95米。这张圆桌的周长是多少米?(得数保留两位小数)
3.14× 0.95
=2.983
≈ 2.98(米)
答:这张圆桌面的周长约是2.98米。
一个圆形水池,周长是9.42米。它的直径是多少米?半径呢?
周长÷π=直径 直径÷2=半径
应该怎样思考
周长=π×直径
9.42÷3.14=3(m)
3÷2=1.5(m)
答:它的直径是3米,半径1.5m.
生命因每天收获知识的果实而快乐成长。
今天你有学会了什么?
我的收获
(1)今天我学习了圆周长的知识。我知道圆周率是( )和( )的比值,它用字母( )表示,它是我国古代数学家( )发现的。
直径d
π≈3.14
周长
直径
祖冲之
(2)我还知道圆的周长总是直径的( )倍。已知圆的直径就可以用公式( )求周长;已知圆的半径就可以用公式( )求周长。
π
C=
d
π
C=
r
2π
π
圆
的
周
长
思考:什么是平面图形周长?
围成一个平面图形所有边长的总和叫做这个图形的周长。
计算下面图形的周长
30厘米
45厘米
20
厘
米
想一想:什么叫圆的周长?
围成圆的曲线的长叫做圆的周长。
用线绕圆片一周,量它的长度。
0
1
2
3
4
6
7
8
5
圆片向右滚动一周,量它的长度。
0
1
2
3
4
6
7
8
5
2厘米
刚才我们用什么办法“化曲为 直”测量呢 ?
一、绕线法
二、滚动法
思考:圆的周长与什么有关系?
让我们来做一个实验,找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填入下表中。看看你有什么发现。
物品名称 周长
(厘米) 直径
(厘米)
(保留两位小数)
直径
直径
直径
直径
直径
直径
直径
直径
直径
是直径的3倍多一些
圆的周长除以直径的商叫做圆周率.用字母π表示
ππ
ππ
ππ
π≈ 3.14
π是个固定的数,
也是个无限不循环小数。
大约2000多年前 我国古代的数学著作《周髀(bì)算经》中就有“周三径一”的记载,意思是说圆的周长大约是直径的3倍
大约1700年前 我国的数学家刘徽(huī)用“割圆术”来求圆周长的近似值。他从圆的内接正六边形算起,逐渐把边数加倍,正十二边形、正二十四边形····· 计算得出圆周率是3.14。并指出,内接正多边形的边数越多,周长越接近圆的周长。直到1200年后,西方人才找到类似的方法。
大约1500年前 我国的数学家祖冲之,计算出圆周率大约在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到6位小数的人。至少要比国外科学家得出这样精确的数值早1000年。
圆的周长总是直径的π倍.
圆周长÷直径= π
圆周长= π × 直径
C = π d
C = 2 π r
1.两个圆的周长相等,那么这两个圆的直径也相等。 ( )
√
2.π=3.14 ( )
×
二、选择填空。
1.车轮滚动一周,前进的距离是求车轮的( )
A.半径 B.直径 C.周长
2.圆的周长是直径的( )倍。
A.3.14 B.π C.3
3.大圆的周长除以直径的商( )小圆的周长 除以直径的商。
A.大于 B.小于 C.等于
C
B
C
一、判断。
5、圆周率与直径的关系是( )。
A、圆周率与直径的长短无关。
B、直径越长,圆周率也就越大。
C、直径越短,圆周率也就越小。
4、在下列各式中,正确的是( )。
A、π>3.14 B、π<3.14 π=3.14
A
A
求下面各圆的周长。
d=4厘米
r=1.5米
3.14×4=12.56(厘米)
3.14×1.5×2=9.42(米)
半径/cm 直径/cm 圆的周长/cm
10
5
24
10
314
6.28
一辆自行车车轮的直径是0.6米。车轮滚动一周,自行车前进多少米?
3.14×0.6=1.884(m)
答:车轮滚动一周,自行车前进1.884m.
摩天轮的半径是5米,坐着它转动一周,大约在空中转过多少米?
3.14×5×2=31.4(米)
答:大约在空中转过31.4米。
一张圆桌面的直径是0.95米。这张圆桌的周长是多少米?(得数保留两位小数)
3.14× 0.95
=2.983
≈ 2.98(米)
答:这张圆桌面的周长约是2.98米。
一个圆形水池,周长是9.42米。它的直径是多少米?半径呢?
周长÷π=直径 直径÷2=半径
应该怎样思考
周长=π×直径
9.42÷3.14=3(m)
3÷2=1.5(m)
答:它的直径是3米,半径1.5m.
生命因每天收获知识的果实而快乐成长。
今天你有学会了什么?
我的收获
(1)今天我学习了圆周长的知识。我知道圆周率是( )和( )的比值,它用字母( )表示,它是我国古代数学家( )发现的。
直径d
π≈3.14
周长
直径
祖冲之
(2)我还知道圆的周长总是直径的( )倍。已知圆的直径就可以用公式( )求周长;已知圆的半径就可以用公式( )求周长。
π
C=
d
π
C=
r
2π
π
