【开学季 分层作业】11.2.3 三角形的外角 同步学案
文档属性
| 名称 | 【开学季 分层作业】11.2.3 三角形的外角 同步学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-28 00:00:00 | ||
图片预览


文档简介
人教版八年级数学上册开学季(第十一章 三角形)分层作业
11.2.3三角形的外角
知识点1三角形外角的定义
1.下列各图中,∠1是△ABC的外角的有( )
A.(l)(2) B.(l)(3) C.(2)(3) D.(2)(4)
2.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
知识点2(三角形外角的性质)
3.[2017贵州黔东南州中考]如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
A.120° B.90° C.100° D.30°
4.[2017四川凉山州中考]如图,AB∥CD,则下列式子一定成立的是( )
A.∠l=∠3 B.∠l=∠3 C.∠1=∠2+∠3 D.∠3=∠1+∠2
5.[2018山东临沂兰陵期中]一副直角三角板拼成如图所示的图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )
A.10° B.15° C.25° D.30°
6.如图,点P是△ABC内一点,连接BP并延长交AC于点D,连接PC,∠l,∠2,∠A的大小关系是( )
A.∠A>∠2>∠l B.∠2>∠A>∠l
C.∠2>∠l>∠A D.∠l>∠2>∠A
7.如图,分别以△ABC的顶点为圆心,1cm长为半径画弧,则图中阴影部分的面积为________cm2.
8.如图,△ABC中,∠A=44°,将△ABC沿EF折叠,点A落在点A'处,则∠1+∠2=_______°.
9.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,若∠B=35°,∠E=20°,求∠BAC的度数.
10.如图,△ABC中,D是BC边上一点,∠l=∠B,∠2=∠C,∠BAC=78°,求∠DAC的度数.
11.如图,已知△ABC中,∠ABC的平分线与△ABC的外角∠ACD的平分线相交于点P.若∠A=70°,求∠P的度数.
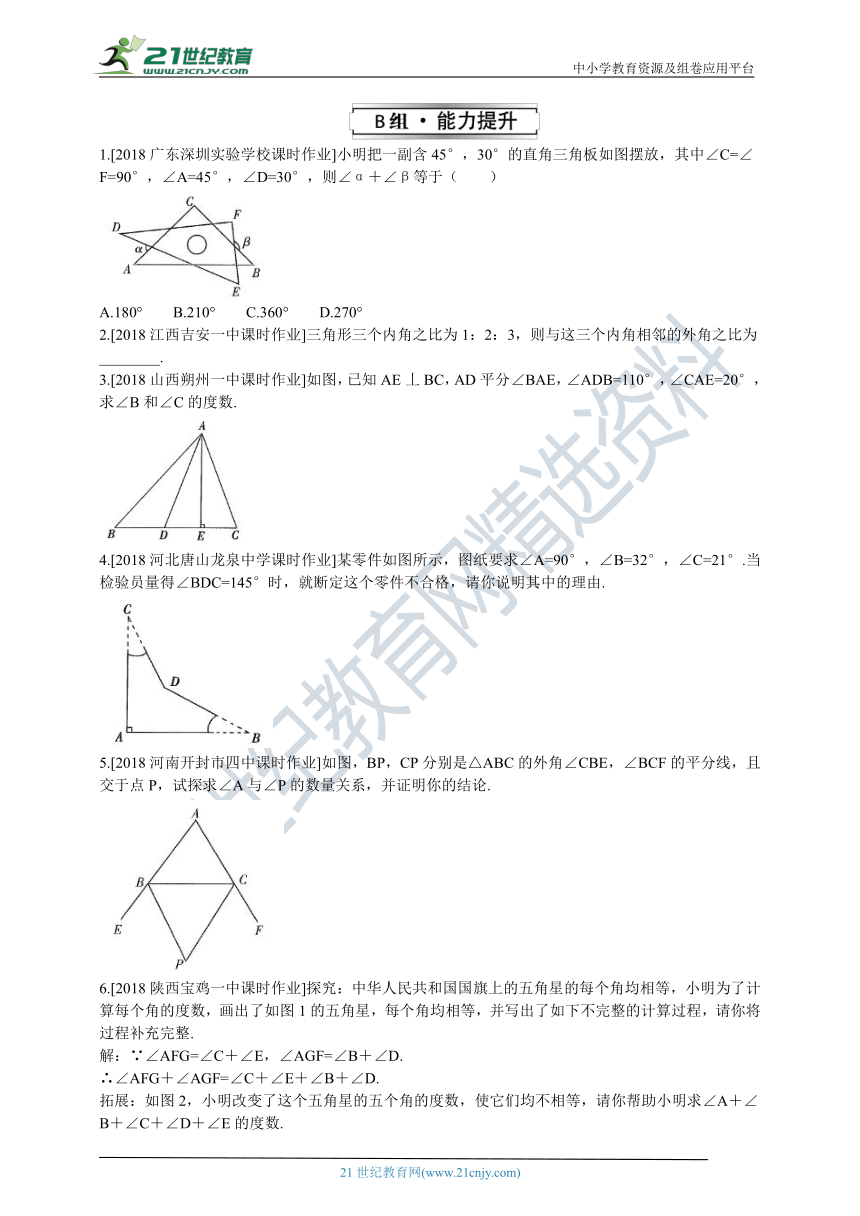
1.[2018广东深圳实验学校课时作业]小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180° B.210° C.360° D.270°
2.[2018江西吉安一中课时作业]三角形三个内角之比为1:2:3,则与这三个内角相邻的外角之比为________.
3.[2018山西朔州一中课时作业]如图,已知AE丄BC,AD平分∠BAE,∠ADB=110°,∠CAE=20°,求∠B和∠C的度数.
4.[2018河北唐山龙泉中学课时作业]某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°.当检验员量得∠BDC=145°时,就断定这个零件不合格,请你说明其中的理由.
5.[2018河南开封市四中课时作业]如图,BP,CP分别是△ABC的外角∠CBE,∠BCF的平分线,且交于点P,试探求∠A与∠P的数量关系,并证明你的结论.
6.[2018陕西宝鸡一中课时作业]探究:中华人民共和国国旗上的五角星的每个角均相等,小明为了计算每个角的度数,画出了如图1的五角星,每个角均相等,并写出了如下不完整的计算过程,请你将过程补充完整.
解:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
拓展:如图2,小明改变了这个五角星的五个角的度数,使它们均不相等,请你帮助小明求∠A+∠B+∠C+∠D+∠E的度数.
应用:如图3,小明将图2中的点A落在BE上,点C落在BD上,.若∠B=∠D=36°,则∠CAD+∠ACE+∠E=______.
参考答案
1.B
【解析】题图(1)中,∠1是△ABC的外角;题图(2)中,∠1是△ABD的外角;题图(3)中,∠1是△ABC的外角;题图(4)中,∠1是△ACE的外角.故选B.
2.C
【解析】若外角小于与它相邻的内角,则内角大于90°,外角小于90°,所以这个三角形中有一个内角为钝角,所以该三角形是钝角三角形.故选C.
3.C
【解析】∵∠ACD=120°,∠B=20°,∴∠A=∠ACD-∠B=120°-20°=100°.故选C.
4.D
【解析】如图,∵AB∥CD,∠3=∠AFC=∠l+∠2.故选D.
5.B
【解析】由题意知∠EDC=60°,∠B=45°.因为∠EDC是△BFD的外角,所以∠BFD=∠EDC-∠B=60°-45°=15°.故选B.
6.D
【解析】根据三角形外角的性质可得∠1=∠2+∠DCP,∠2=∠A+∠ABD,所以∠1>∠2>∠A.故选D.
7.π
【解析】根据三角形的外角和等于360°,可知题图中三个扇形的面积恰好等于半径为1cm的圆的面积,所以图中阴影部分的面积为πcm2.
8.88
【解析】连接AA'根据三角形的外角等于与它不相邻的两个内角的和,可知∠l+∠2=∠BAA'+∠EA'A+∠FAA'+∠FA'A=∠BAC+∠EA'F,∵∠BAC=∠EA'F,∠BAC=44°,∴∠l+∠2=2∠BAC=88°.
9.【解析】∵∠B=35°,∠E=20°,
∴∠ECD=∠B+∠E=55°.
∵CE平分∠ACD,∴∠ACD=2∠ECD=2×55°=110°,
∴∠BAC=∠ACD-∠B=110°-35°=75°.
10.【解析】∵∠BAC+∠B+∠C=180°,
∴∠B+∠C=180°-∠BAC=180°-78°=102°.
∵∠2=∠B+∠l,∠l=∠B,∠C=∠2,∴∠C=2∠l,
∴∠B+∠C=∠l+2∠1=102°,∴∠l=34°,
∴∠DAC=∠BAC-∠l=78°-34°=44°.
11.【解析】∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠ABC=70°+∠ABC.
∵CP是∠ACD的平分线,
∴∠DCP=∠ACD=(70°+∠ABC)=35°+∠ABC.
∵BP是∠ABC的平分线,∴∠CBP=∠ABC.
∵∠DCP是△BCP的外角,
∴∠DCP=∠CBP+∠P=∠ABC+∠P=∠ABC+35°,
∴∠P=35°.
l.B
【解析】如图,∵∠α=∠D+∠DGA=30°+∠CGH,∠β=∠F+∠FHB二90°+∠CHG,∴∠α+∠β=30°+∠CGH+90°+∠CHG=120°+(∠CGH+∠CHG)=120°+90°=210°.故选B.
2.5:4:3
【解析】设三角形三个内角分别为x,2x,3x,则x+2x+3x=180°,解得x=30°,则与三个内角相邻的外角的度数分别为180°-x=150°,180°-2x=120°,180°-3x=90°,它们的比为150°:120°:90°=5:4:3.
3.【解析】∵AE丄BC,∠CAE=20°,
∴∠C=90°-20°=70°.
∵AD平分∠BAE,∴∠BAD=∠DAE.
∵∠ADB=110°,
∴∠DAE=∠ADB-∠AED=110°-90°=20°,
∴∠BAD=∠DAE=20°,
∴∠BAE=40°,∴∠B=90°-∠BAE=90°-40°=50°.
4.【解析】理由如下:
如图,延长CD交AB于点E.
∵∠BED=∠A+∠C,
∠BDC=∠BED+∠B,
∴∠BDC=∠A+∠B+∠C=90°+32°+21°=143°.
∵∠BDC=145°,∴这个零件不合格.
5.【解析】2∠P+∠A=180°
证明:∵∠P+∠PBC+∠PCB=180°,
∴2∠P+2∠PBC+2∠PCB=360°
∵BP平分∠CBE,CP平分∠BCF,
∴∠CBE=2∠PBC,∠BCF=2∠PCB,
∵2∠P+∠CBE+∠BCF=360°,
又∠CBE=∠A+∠ACB,∠BCF=∠A+∠ABC,
∴2∠P+(∠A+∠ACB)+(∠A+∠ABC)=360°①,
又∠A+∠ABC+∠ACB=180°②,
∴①—②得2∠P+∠A=18°
6.【解析】
探究:需要补充的解题过程如下.
∵∠A+∠AFG+∠AGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
又∠A=∠B=∠C=∠D=∠E,
∴∠A=∠B=∠C=∠D=∠E=36°.
拓展:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D,
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=180°,
∴∠A+∠C+∠E+∠B+∠D=180°,即∠A+∠B+∠C+∠D+∠E=180°.
应用:l08°
∵∠EAD=∠B+∠D,∠CAE+∠ACE+∠E=180°,
∴∠CAD+∠ACE+∠E=180°-∠EAD=180°-∠B-∠D=108°.
名师点睛:掌握三角形内角和定理及三角形外角的性质是解题的关键.
11.2.3三角形的外角
知识点1三角形外角的定义
1.下列各图中,∠1是△ABC的外角的有( )
A.(l)(2) B.(l)(3) C.(2)(3) D.(2)(4)
2.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
知识点2(三角形外角的性质)
3.[2017贵州黔东南州中考]如图,∠ACD=120°,∠B=20°,则∠A的度数是( )
A.120° B.90° C.100° D.30°
4.[2017四川凉山州中考]如图,AB∥CD,则下列式子一定成立的是( )
A.∠l=∠3 B.∠l=∠3 C.∠1=∠2+∠3 D.∠3=∠1+∠2
5.[2018山东临沂兰陵期中]一副直角三角板拼成如图所示的图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )
A.10° B.15° C.25° D.30°
6.如图,点P是△ABC内一点,连接BP并延长交AC于点D,连接PC,∠l,∠2,∠A的大小关系是( )
A.∠A>∠2>∠l B.∠2>∠A>∠l
C.∠2>∠l>∠A D.∠l>∠2>∠A
7.如图,分别以△ABC的顶点为圆心,1cm长为半径画弧,则图中阴影部分的面积为________cm2.
8.如图,△ABC中,∠A=44°,将△ABC沿EF折叠,点A落在点A'处,则∠1+∠2=_______°.
9.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,若∠B=35°,∠E=20°,求∠BAC的度数.
10.如图,△ABC中,D是BC边上一点,∠l=∠B,∠2=∠C,∠BAC=78°,求∠DAC的度数.
11.如图,已知△ABC中,∠ABC的平分线与△ABC的外角∠ACD的平分线相交于点P.若∠A=70°,求∠P的度数.
1.[2018广东深圳实验学校课时作业]小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180° B.210° C.360° D.270°
2.[2018江西吉安一中课时作业]三角形三个内角之比为1:2:3,则与这三个内角相邻的外角之比为________.
3.[2018山西朔州一中课时作业]如图,已知AE丄BC,AD平分∠BAE,∠ADB=110°,∠CAE=20°,求∠B和∠C的度数.
4.[2018河北唐山龙泉中学课时作业]某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°.当检验员量得∠BDC=145°时,就断定这个零件不合格,请你说明其中的理由.
5.[2018河南开封市四中课时作业]如图,BP,CP分别是△ABC的外角∠CBE,∠BCF的平分线,且交于点P,试探求∠A与∠P的数量关系,并证明你的结论.
6.[2018陕西宝鸡一中课时作业]探究:中华人民共和国国旗上的五角星的每个角均相等,小明为了计算每个角的度数,画出了如图1的五角星,每个角均相等,并写出了如下不完整的计算过程,请你将过程补充完整.
解:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
拓展:如图2,小明改变了这个五角星的五个角的度数,使它们均不相等,请你帮助小明求∠A+∠B+∠C+∠D+∠E的度数.
应用:如图3,小明将图2中的点A落在BE上,点C落在BD上,.若∠B=∠D=36°,则∠CAD+∠ACE+∠E=______.
参考答案
1.B
【解析】题图(1)中,∠1是△ABC的外角;题图(2)中,∠1是△ABD的外角;题图(3)中,∠1是△ABC的外角;题图(4)中,∠1是△ACE的外角.故选B.
2.C
【解析】若外角小于与它相邻的内角,则内角大于90°,外角小于90°,所以这个三角形中有一个内角为钝角,所以该三角形是钝角三角形.故选C.
3.C
【解析】∵∠ACD=120°,∠B=20°,∴∠A=∠ACD-∠B=120°-20°=100°.故选C.
4.D
【解析】如图,∵AB∥CD,∠3=∠AFC=∠l+∠2.故选D.
5.B
【解析】由题意知∠EDC=60°,∠B=45°.因为∠EDC是△BFD的外角,所以∠BFD=∠EDC-∠B=60°-45°=15°.故选B.
6.D
【解析】根据三角形外角的性质可得∠1=∠2+∠DCP,∠2=∠A+∠ABD,所以∠1>∠2>∠A.故选D.
7.π
【解析】根据三角形的外角和等于360°,可知题图中三个扇形的面积恰好等于半径为1cm的圆的面积,所以图中阴影部分的面积为πcm2.
8.88
【解析】连接AA'根据三角形的外角等于与它不相邻的两个内角的和,可知∠l+∠2=∠BAA'+∠EA'A+∠FAA'+∠FA'A=∠BAC+∠EA'F,∵∠BAC=∠EA'F,∠BAC=44°,∴∠l+∠2=2∠BAC=88°.
9.【解析】∵∠B=35°,∠E=20°,
∴∠ECD=∠B+∠E=55°.
∵CE平分∠ACD,∴∠ACD=2∠ECD=2×55°=110°,
∴∠BAC=∠ACD-∠B=110°-35°=75°.
10.【解析】∵∠BAC+∠B+∠C=180°,
∴∠B+∠C=180°-∠BAC=180°-78°=102°.
∵∠2=∠B+∠l,∠l=∠B,∠C=∠2,∴∠C=2∠l,
∴∠B+∠C=∠l+2∠1=102°,∴∠l=34°,
∴∠DAC=∠BAC-∠l=78°-34°=44°.
11.【解析】∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠ABC=70°+∠ABC.
∵CP是∠ACD的平分线,
∴∠DCP=∠ACD=(70°+∠ABC)=35°+∠ABC.
∵BP是∠ABC的平分线,∴∠CBP=∠ABC.
∵∠DCP是△BCP的外角,
∴∠DCP=∠CBP+∠P=∠ABC+∠P=∠ABC+35°,
∴∠P=35°.
l.B
【解析】如图,∵∠α=∠D+∠DGA=30°+∠CGH,∠β=∠F+∠FHB二90°+∠CHG,∴∠α+∠β=30°+∠CGH+90°+∠CHG=120°+(∠CGH+∠CHG)=120°+90°=210°.故选B.
2.5:4:3
【解析】设三角形三个内角分别为x,2x,3x,则x+2x+3x=180°,解得x=30°,则与三个内角相邻的外角的度数分别为180°-x=150°,180°-2x=120°,180°-3x=90°,它们的比为150°:120°:90°=5:4:3.
3.【解析】∵AE丄BC,∠CAE=20°,
∴∠C=90°-20°=70°.
∵AD平分∠BAE,∴∠BAD=∠DAE.
∵∠ADB=110°,
∴∠DAE=∠ADB-∠AED=110°-90°=20°,
∴∠BAD=∠DAE=20°,
∴∠BAE=40°,∴∠B=90°-∠BAE=90°-40°=50°.
4.【解析】理由如下:
如图,延长CD交AB于点E.
∵∠BED=∠A+∠C,
∠BDC=∠BED+∠B,
∴∠BDC=∠A+∠B+∠C=90°+32°+21°=143°.
∵∠BDC=145°,∴这个零件不合格.
5.【解析】2∠P+∠A=180°
证明:∵∠P+∠PBC+∠PCB=180°,
∴2∠P+2∠PBC+2∠PCB=360°
∵BP平分∠CBE,CP平分∠BCF,
∴∠CBE=2∠PBC,∠BCF=2∠PCB,
∵2∠P+∠CBE+∠BCF=360°,
又∠CBE=∠A+∠ACB,∠BCF=∠A+∠ABC,
∴2∠P+(∠A+∠ACB)+(∠A+∠ABC)=360°①,
又∠A+∠ABC+∠ACB=180°②,
∴①—②得2∠P+∠A=18°
6.【解析】
探究:需要补充的解题过程如下.
∵∠A+∠AFG+∠AGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
又∠A=∠B=∠C=∠D=∠E,
∴∠A=∠B=∠C=∠D=∠E=36°.
拓展:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D,
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=180°,
∴∠A+∠C+∠E+∠B+∠D=180°,即∠A+∠B+∠C+∠D+∠E=180°.
应用:l08°
∵∠EAD=∠B+∠D,∠CAE+∠ACE+∠E=180°,
∴∠CAD+∠ACE+∠E=180°-∠EAD=180°-∠B-∠D=108°.
名师点睛:掌握三角形内角和定理及三角形外角的性质是解题的关键.
